Эргодическая марковская цепь

Определение:

Эргодическая марковская цепь — марковская цепь, целиком состоящая из одного эргодического класса.

Стационарный режим

Эргодические марковские цепи описываются сильно связным графом. Это означает, что в такой системе возможен переход из любого состояния [math]S_i[/math] в любое состояние [math]S_{j}, (i,j = 1,2,...,n)[/math] за конечное число шагов.

Для эргодических цепей при достаточно большом времени функционирования ([math]t \to \infty[/math]) наступает стационарный режим, при котором вероятности [math]\alpha_i[/math] состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, то есть: [math]\alpha_i = const[/math].

Классификация эргодических цепей

Определение:

В эргодической цепи можно выделить циклические классы. Количество циклических классов [math] d [/math] называют периодом цепи, если цепь состоит целиком из одного циклического класса, её называют регулярной. С течением времени текущее состояние движется по циклическим классам в определенном порядке, причем каждые d шагов она оказывается в одном и том же циклическом классе.

Таким образом, эргодические цепи делятся на регулярные и циклические.

Эргодическая теорема

Определение:

Эргодическое (стационарное) распределение — распределение [math]\alpha = (\alpha_1 \dots \alpha_n )[/math], такое что [math]\alpha_i \gt 0[/math] и [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \alpha_j[/math] (где [math]p_{ij}^{(n)}[/math] — вероятность оказаться в [math]j[/math]-ом состоянии, выйдя из [math]i[/math]-ого, через [math]n[/math] переходов).

Для регулярных цепей

Доказательство теоремы для случая регулярных цепей приведено в конспекте про регулярные цепи.

Для циклических цепей

Теорема (Эргодическая теорема):

Для любой эргодической цепи последовательность степеней [math]P^{n}[/math] суммируется по Эйлеру к предельной матрице [math]A[/math], и эта предельная матрица имеет вид [math]A = \xi\alpha[/math], где [math]\alpha[/math] — положительный вероятностный вектор, [math]\xi[/math] - вектор-столбец из единиц.

Доказательство:

[math]\triangleright[/math]

В случае циклической цепи переходы из одного циклического класса в другой возможны только при определенных значениях [math] n [/math], которые периодически повторяются. Таким образом, никакая степень матрицы переходов [math]P[/math] не является положительной матрицей, и различные степени содержат нули на различных местах. С увеличением степени расположение этих нулей периодически повторяется. Следовательно, последовательность [math]P^{n}[/math] не может сходиться в обычном смысле, для нее требуется так называемая суммируемость по Эйлеру. Рассмотрим матрицу [math](kI + (1 - k)P)[/math] при некотором [math]k, ~ 0 \lt k \lt 1[/math]. Эта матрица является переходной матрицей. Она имеет положительные элементы на всех тех же местах, что и [math]P[/math], следовательно, она также задает эргодическую цепь. Также диагональные элементы этой матрицы положительны. Значит, в каждое состояние можно возвратиться за один шаг, а это значит, что [math]d = 1[/math]. Таким образом, новая цепь является регулярной. Из эргодической теоремы для регулярных цепей следует, что [math](kI + (1 - k)P)^{n}[/math] стремится к матрице [math]A = \xi\alpha[/math], где [math]\alpha[/math] — положительный вероятностный вектор. Таким образом: [math] A = \lim\limits_{x\to \infty} (kI + (1 - k)P)^{n}[/math] [math] A = \lim\limits_{x\to \infty} \sum\limits_{i = 0}^{n} {n\choose i} k^{n - i} (1 - k)^{i} P^{i} ~~~~~ (1)[/math] Но последнее равенство в точности означает, что последовательность [math]P^{n}[/math] суммируема по Эйлеру к [math]A[/math], причем суммируема при каждом значении [math]k[/math].

[math]\triangleleft[/math]

Следствия

Теорема:

Если [math]P, A, \alpha[/math] — объекты из предыдущей теоремы. Тогда справедливы факты: Для любого вероятностного вектора [math]\pi[/math] последовательность [math]\pi P^{n}[/math] суммируема по Эйлеру к [math]\alpha[/math] Вектор [math]\alpha[/math] является единственным неподвижным вектором матрицы [math]P[/math] [math]PA = AP = A[/math]

Доказательство:

[math]\triangleright[/math]

Домножим [math](1)[/math] на [math]\pi[/math]. Таким образом, мы получим, что предел последовательности [math]\pi P^{n}[/math] в смысле Эйлера равен [math]\pi A = \pi \xi \alpha[/math]. Значит, первый факт доказан. Так как вектор [math]\alpha[/math] был получен из предельной матрицы для [math](kI + (1 - k)P)[/math], являющейся регулярной переходной матрицей, то он будет её единственным неподвижным вероятностным вектором. Но матрица [math](kI + (1 - k)P)[/math] должна иметь те же неподвижные векторы, что и [math]P[/math], так как из соотношения [math]\pi (kI + (1 - k)P) = \pi[/math], следует, что [math]\pi (1 - k) P = \pi (1 - k)[/math] и поскольку [math]k \ne 1[/math], то [math]\pi P = \pi[/math]. Получается, что второй факт доказан. Третий факт следует из того, что [math]P \xi = \xi[/math] для любой переходной матрицы и что [math]\alpha P = \alpha[/math].

[math]\triangleleft[/math]

Пример

Пример циклической цепи

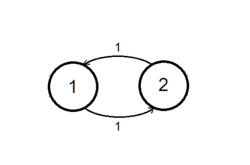
Самым простым примером циклической цепи является цепь из двух состояний, с переходной матрицей:

[math]P = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}[/math] .

Стационарным распределением этой цепи будет [math] \alpha = (0.5, 0.5) [/math].

Ссылки

• Эргодическое распределение — Википедия

• Дискретное распределение — Википедия

• Суммируемость по Эйлеру — Википедия

Источники информации

• Дж. Кемени, Дж. Снелл "Конечные цепи Маркова" - Издательство "Наука", 1970 г - 129 c.