Кластеризация
Кластеризация (англ. cluster analysis) — задача группировки множества объектов на подмножества (кластеры) таким образом, чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров по какому-либо критерию.
Задача кластеризации относится к классу задач обучения без учителя.
Содержание
Постановка задачи кластеризации
Пусть — множество объектов, — множество идентификаторов (меток) кластеров. На множестве задана функция расстояния между объектами . Дана конечная обучающая выборка объектов . Необходимо разбить выборку на подмножества (кластеры), то есть каждому объекту сопоставить метку , таким образом чтобы объекты внутри каждого кластера были близки относительно метрики , а объекты из разных кластеров значительно различались.
| Определение: |
| Алгоритм кластеризации — это функция , которая любому объекту ставит в соответствие идентификатор кластера . |
Множество в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки объектов из обучающей выборки изначально не заданы, и даже может быть неизвестно само множество .
Решение задачи кластеризации объективно неоднозначно по ряду причин:
- не существует однозначного критерия качества кластеризации. Известен ряд алгоритмов, осуществляющих разумную кластеризацию "по построению", однако все они могут давать разные результаты. Следовательно, для определения качества кластеризации и оценки выделенных кластеров необходим эксперт предметной области.
- число кластеров, как правило, заранее не известно и выбирается по субъективным критериям. Даже если алгоритм не требует изначального знания о числе классов, конкретные реализации зачастую требуют ввести этот параметр[1].
- результат кластеризации существенно зависит от метрики. Однако существует ряд рекомендаций по выбору для определенных классов задач.
Типология задач кластеризации
Типы входных данных
- Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками (англ. features). Признаки могут быть как числовыми, так и нечисловыми.
- Матрица расстояний между объектами. Каждый объект описывается расстоянием до всех объектов из обучающей выборки.
Вычисление матрицы расстояний по признаковому описанию объектов может быть выполнено бесконечным числом способов в зависимости от определения метрики между объектами. Выбор метрики зависит от обучающей выборки и поставленной задачи.
Цели кластеризации
- Классификация объектов. Попытка понять зависимости между объектами путем выявления их кластерной структуры. Разбиение выборки на группы схожих объектов упрощает дальнейшую обработку данных и принятие решений, позволяет применить к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»). В данном случае стремятся уменьшить число кластеров для выявления наиболее общих закономерностей.
- Сжатие данных. Можно сократить размер исходной выборки, взяв один или несколько наиболее типичных представителей каждого кластера. Здесь важно наиболее точно очертить границы каждого кластера, их количество не является важным критерием.
- Обнаружение новизны (обнаружение шума). Выделение объектов, которые не подходят по критериям ни в один кластер. Обнаруженные объекты в дальнейшем обрабатывают отдельно.
Методы кластеризации
- Графовые алгоритмы кластеризации. Наиболее примитивный класс алгоритмов. В настоящее время практически не применяется на практике.
- Вероятностные алгоритмы кластеризации. Каждый объект из обучающей выборки относится к каждому из кластеров с определенной степенью вероятности.
- Алгоритм средних (англ. means)
- EM-алгоритм
- Иерархические алгоритмы кластеризации. Упорядочивание данных путем создания иерархии вложенных кластеров.
Иерархическая кластеризация
Пример
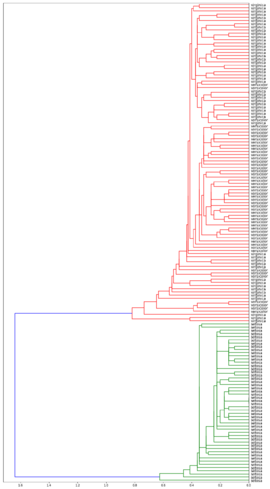
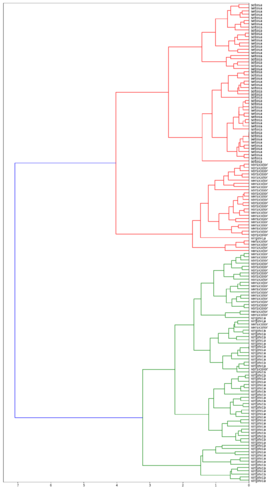
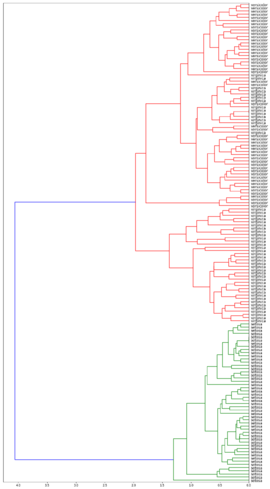
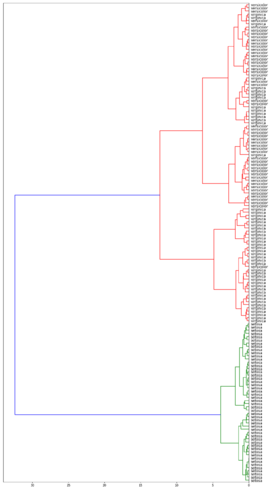
| Дендрограммы кластеризации ирисов Фишера[2] в зависимости от функции расстояния между кластерами | |||
|
|
|
|
| Расстояние минимума | Расстояние максимума | Расстояние среднего | Расстояние Уорда |
Лучше всего с задачей справился алгоритм с использованием расстояния Уорда. Он точно выделил класс Iris setosa и заметно отделили вид Iris virginica от Iris versicolor.