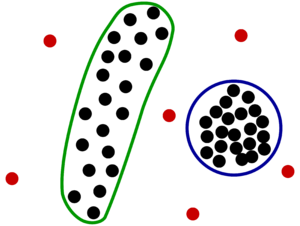
Кластеризация

Пример кластеризации. Красным цветом выделены неклассифицированные объекты.

Кластеризация (англ. cluster analysis) — задача группировки множества объектов на подмножества (кластеры) таким образом, чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров по какому-либо критерию.

Задача кластеризации относится к классу задач обучения без учителя.

Постановка задачи кластеризации

Пусть [math]X[/math] — множество объектов, [math]Y[/math] — множество идентификаторов (меток) кластеров. На множестве [math]X[/math] задана функция расстояния между объектами [math]\rho(x,x')[/math]. Дана конечная обучающая выборка объектов [math]X^m = \{ x_1, \dots, x_m \} \subset X[/math]. Необходимо разбить выборку на подмножества (кластеры), то есть каждому объекту [math]x_i \in X^m[/math] сопоставить метку [math]y_i \in Y[/math], таким образом чтобы объекты внутри каждого кластера были близки относительно метрики [math]\rho[/math], а объекты из разных кластеров значительно различались.

Определение:

Алгоритм кластеризации — функция [math]a\colon X\to Y[/math], которая любому объекту [math]x\in X[/math] ставит в соответствие идентификатор кластера [math]y\in Y[/math].

Множество [math]Y[/math] в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.

Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки объектов из обучающей выборки [math]y_i[/math] изначально не заданы, и даже может быть неизвестно само множество [math]Y[/math].

Решение задачи кластеризации объективно неоднозначно по ряду причин:

• не существует однозначного критерия качества кластеризации. Известен ряд алгоритмов, осуществляющих разумную кластеризацию "по построению", однако все они могут давать разные результаты. Следовательно, для определения качества кластеризации и оценки выделенных кластеров необходим эксперт предметной области.
• число кластеров, как правило, заранее не известно и выбирается по субъективным критериям. Даже если алгоритм не требует изначального знания о числе классов, конкретные реализации зачастую требуют указать этот параметр.
• результат кластеризации существенно зависит от метрики. Однако существует ряд рекомендаций по выбору метрик для определенных классов задач.

Типология задач кластеризации

Типы входных данных

• Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками (англ. features). Признаки могут быть как числовыми, так и нечисловыми.
• Матрица расстояний между объектами. Каждый объект описывается расстоянием до всех объектов из обучающей выборки.

Вычисление матрицы расстояний по признаковому описанию объектов может быть выполнено бесконечным числом способов в зависимости от определения метрики между объектами. Выбор метрики зависит от обучающей выборки и поставленной задачи.

Цели кластеризации

• Классификация объектов. Попытка понять зависимости между объектами путем выявления их кластерной структуры. Разбиение выборки на группы схожих объектов упрощает дальнейшую обработку данных и принятие решений, позволяет применить к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»). В данном случае стремятся уменьшить число кластеров для выявления наиболее общих закономерностей.
• Сжатие данных. Можно сократить размер исходной выборки, взяв один или несколько наиболее типичных представителей каждого кластера. Здесь важно наиболее точно очертить границы каждого кластера, их количество не является важным критерием.
• Обнаружение новизны (обнаружение шума). Выделение объектов, которые не подходят по критериям ни в один кластер. Обнаруженные объекты в дальнейшем обрабатывают отдельно.

Методы кластеризации

• Графовые алгоритмы кластеризации. Наиболее примитивный класс алгоритмов. В настоящее время практически не применяется на практике.
• Вероятностные алгоритмы кластеризации. Каждый объект из обучающей выборки относится к каждому из кластеров с определенной степенью вероятности.
  • Алгоритм [math]k-[/math]средних (англ. [math]k-[/math]means)
  • EM-алгоритм
• Иерархические алгоритмы кластеризации. Упорядочивание данных путем создания иерархии вложенных кластеров.

Применение

Биология и биоинформатика

• В области экологии кластеризация используется для выделения пространственных и временных сообщест организмов в однородных условиях.
• Кластерный анализ используется для группировки схожих геномных последовательностей в семейство генов, которые являются консервативными структурами для многих организмов и могут выполнять схожие функции.
• Кластеризация помогает автоматически определять генотипы по различным частям хромосом.
• Алгоритмы применяются для выделения небольшого числа групп генетических вариации человеческого генома.

Медицина

• Используется в позитронно-эмиссионной томографии для автоматического выделения различных типов тканей на трехмерном изображении.
• Применяется для выявления шаблонов устойчивости к антибиотикам; для классификации антибиотиков по типу антибактериальной активности.

Маркетинг

Кластеризация широко используется при изучении рынка для обработки данных, полученных из различных опросов. Может применяться для выделения типичных групп покупателей, разделения рынка для создания персонализированных предложений, разработки новых линий продукции.

Интернет

• Выделение групп людей на основе графа связей в социальных сетях.
• Повышение релевантности ответов на поисковые запросы путем группировки веб-сайтов по смысловым значениям поискового запроса.

Компьютерные науки

• Кластеризация используется в сегментации изображений для определения границ и распознавания объектов.
• Кластерный анализ применяется для определения образовавшихся популяционных ниш в ходе работы эволюционных алгоритмов для улучшения параметров эволюции.
• Подбор рекомендаций для пользователя на основе предпочтений других пользователей в данном кластере.
• Определение аномалий путем построения кластеров и выявления неклассифицированных объектов.

Иерархическая кластеризация

Определение:

Иерархическая кластеризация (англ. hierarchical clustering) — множество алгоритмов кластеризации, направленных на создание иерархии вложенных разбиений исходного множества объектов.

Иерархические алгоритмы кластеризации часто называют алгоритмами таксономии. Для визуального представления результатов кластеризации используется дендрограмма — дерево, построенное по матрице мер близости между кластерами. В узлах дерева находятся подмножества объектов из обучающей выборки. При этом на каждом ярусе дерева множество объектов из всех узлов составляет исходное множество объектов. Объединение узлов между ярусами соответствует слиянию двух кластеров. При этом длина ребра соответствует расстоянию между кластерами.

Дерево строится от листьев к корню. В начальный момент времени каждый объект содержится в собственном кластере. Далее происходит итеративный процесс слияния двух ближайших кластеров до тех пор, пока все кластеры не объединятся в один или не будет найдено необходимое число кластеров. На каждом шаге необходимо уметь вычислять расстояние между кластерами и пересчитывать расстояние между новыми кластерами. Расстояние между одноэлементными кластерами определяется через расстояние между объектами: [math]\mathrm{R}(\{x\}, \{y\}) = \rho(x, y)[/math]. Для вычисления расстояния [math]\mathrm{R}(U, V)[/math] между кластерами [math]\mathrm{U}[/math] и [math]\mathrm{V}[/math] на практике используются различные функции в зависимости от специфики задачи.

Функции расстояния между кластерами

• Метод одиночной связи (англ. single linkage)

[math]\mathrm{R_{min}}(U, V) = \displaystyle\min_{u \in U, v \in V} \rho(u, v)[/math]

• Метод полной связи (англ. complete linkage)

[math]\mathrm{R_{max}}(U, V) = \displaystyle\max_{u \in U, v \in V} \rho(u, v)[/math]

• Метод средней связи (англ. UPGMA (Unweighted Pair Group Method with Arithmetic mean))

[math]\mathrm{R_{avg}}(U, V) = \displaystyle\dfrac{1}{|U| \cdot |V|}\sum_{u \in U} \sum_{v \in V} \rho(u, v)[/math]

• Центроидный метод (англ. UPGMC (Unweighted Pair Group Method with Centroid average))

[math]\mathrm{R_{c}}(U, V) = \displaystyle\rho^2\left(\sum_{u \in U}\dfrac{u}{|U|}, \sum_{v \in V}\dfrac{v}{|V|}\right)[/math]

• Метод Уорда (англ. Ward's method)

[math]\mathrm{R_{ward}}(U, V) = \displaystyle\dfrac{|U| \cdot |V|}{|U| + |V|}\rho^2\left(\sum_{u \in U}\dfrac{u}{|U|}, \sum_{v \in V}\dfrac{v}{|V|}\right)[/math]

Формула Ланса-Уильямса

На каждом шаге необходимо уметь быстро подсчитывать расстояние от образовавшегося кластера [math]\mathrm{W}=\mathrm{U}\cup\mathrm{V}[/math] до любого другого кластера [math]\mathrm{S}[/math], используя известные расстояния с предыдущих шагов. Это легко выполняется при использовании формулы, предложенной Лансом и Уильямсом в 1967 году:

[math]\mathrm{R}(W, S) = \alpha_U \cdot \mathrm{R}(U, S) + \alpha_V \cdot \mathrm{R}(V, S) + \beta \cdot \mathrm{R}(U, V) + \gamma \cdot |\mathrm{R}(U, S) - \mathrm{R}(V, S)| [/math]

, где [math]\alpha_U, \alpha_V, \beta, \gamma [/math] — числовые параметры.

Каждая из указанных выше функций расстояния удовлетворяет формуле Ланса-Уильямса со следующими коэффициентами:

• Метод одиночной связи (англ. single linkage)

[math]\alpha_U = \dfrac{1}{2}, \alpha_V = \dfrac{1}{2}, \beta = 0, \gamma = -\dfrac{1}{2}[/math]

• Метод полной связи (англ. complete linkage)

[math]\alpha_U = \dfrac{1}{2}, \alpha_V = \dfrac{1}{2}, \beta = 0, \gamma = \dfrac{1}{2} [/math]

• Метод средней связи (англ. UPGMA (Unweighted Pair Group Method with Arithmetic mean))

[math]\alpha_U = \dfrac{|U|}{|W|}, \alpha_V = \dfrac{|V|}{|W|}, \beta = 0, \gamma = 0 [/math]

• Центроидный метод (англ. UPGMC (Unweighted Pair Group Method with Centroid average))

[math]\alpha_U = \dfrac{|U|}{|W|}, \alpha_V = \dfrac{|V|}{|W|}, \beta = -\alpha_U \cdot \alpha_V, \gamma = 0[/math]

• Метод Уорда (англ. Ward's method)

[math]\alpha_U = \dfrac{|S|+|U|}{|S|+|W|}, \alpha_V = \dfrac{|S|+|V|}{|S|+|W|}, \beta = \dfrac{-|S|}{|S|+|W|}, \gamma = 0 [/math]

Свойство монотонности

Введем обозначение [math]\mathrm{R_t}[/math] — расстояние между кластерами, выбранными на шаге [math]t[/math] для объединения.

Дендрограмма позволяет представлять зависимости между множеством объектов с любым числом заданных характеристик на двумерном графике, где по одной из осей откладываются все объекты, а по другой — расстояние [math]\mathrm{R_t}[/math]. Если не накладывать на это расстояние никаких ограничений, то дендрограмма будет иметь большое число самопересечений и изображение перестанет быть наглядным. Чтобы любой кластер мог быть представлен в виде непрерывного отрезка на оси объектов и ребра не пересекались, необходимо наложить ограничение монотонности на [math]\mathrm{R_t}[/math].

Определение:

Функция расстояния [math]\mathrm{R}[/math] является монотонной, если на каждом следующем шаге расстояние между кластерами не уменьшается: [math]\mathrm{R_2} \leqslant \mathrm{R_3} \leqslant \dots \leqslant \mathrm{R_m}[/math]

Расстояние является монотонным, если для коэффициентов в формул Ланса-Уильямса верна теорема Миллигана.

Теорема (Миллиган, 1979):

Если выполняются следующие три условия, то кластеризация является монотонной: [math]\alpha_U \geqslant 0, \alpha_V \geqslant 0 [/math]; [math]\alpha_U + \alpha_V + \beta \geqslant 1[/math]; [math]\min\{\alpha_U, \alpha_V\} + \gamma \geqslant 0 [/math].

Из перечисленных выше расстояний теореме удовлетворяют все, кроме центроидного.

Определение числа кластеров

Для определения числа кластеров находится интервал максимальной длины [math]|\mathrm{R_{t+1}} - \mathrm{R_t}|[/math]. В качестве итоговых кластеров выдаются кластеры, полученные на шаге [math]\mathrm{t}[/math]. При этом число кластеров равно [math]m - t + 1[/math].

Однако, когда число кластеров заранее неизвестно и объектов в выборке не очень много, бывает полезно изучить дендрограмму целиком.

Псевдокод

// алгоритм принимает множество объектов и возвращает множество кластеров для каждого шага 
function hierarchy(X: Set<Object>): Set<Set<Object>>
  t = 1
  [math]\mathrm{C_t} = {{x_1}, \dots, {x_m}}[/math]
  for i = 2 to m
     [math]\langle U, V \rangle = \displaystyle \arg \min_{U \neq V, U \in C_{i-1}, V \in C_{i-1}} R(U, V)[/math]
     [math]\mathrm{R_{t}} = \mathrm{R}(U, V)[/math]
     [math]\mathrm{C_{i}} = \mathrm{C_{i-1}} \cup \{\mathrm{W}\} \setminus \{\mathrm{U}, \mathrm{V}\}[/math]
     for [math] S [/math] in [math] C_t [/math] 
         [math]\mathrm{R_{i}}(W, S) = \alpha_U \cdot \mathrm{R_{i-1}}(U, S) + \alpha_V \cdot \mathrm{R_{i-1}}(V, S) + \beta \cdot \mathrm{R_{i-1}}(U, V) + \gamma \cdot |\mathrm{R_{i-1}}(U, S) - \mathrm{R{i-1}}(V, S)| [/math]
  return [math] C [/math]

Пример

# Подключение библиотек
from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn import datasets
import matplotlib.pyplot as plt
[math][/math]
# Создание полотна для рисования
fig = plt.figure(figsize=(15, 30))
fig.patch.set_facecolor('white')
[math][/math]
# Загрузка набора данных "Ирисы Фишера"
iris = datasets.load_iris()
[math][/math]
# Реализация иерархической кластеризации при помощи функции linkage
mergings = linkage(iris.data, method='ward')
[math][/math]
# Построение дендрограммы. Разными цветами выделены автоматически определенные кластеры
R = dendrogram(mergings, labels=[iris.target_names[i] for i in iris.target], orientation = 'left', leaf_font_size = 12)
[math][/math]
# Отображение дендрограммы
plt.show()

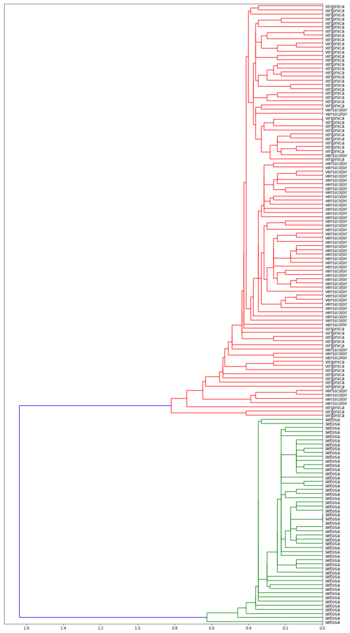
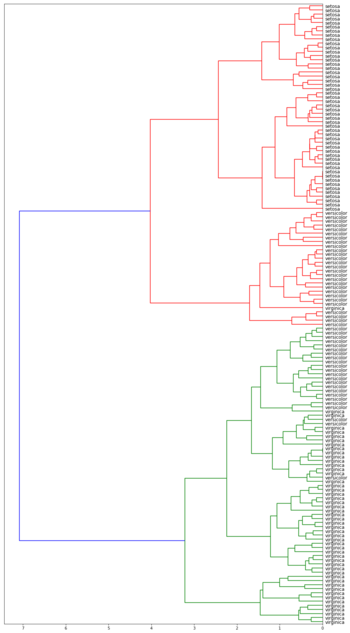
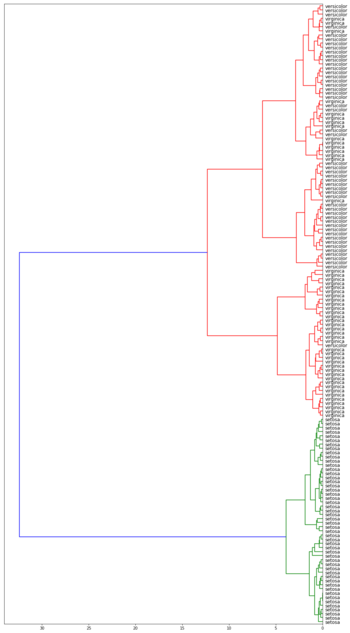
Дендрограммы кластеризации ирисов Фишера в зависимости от функции расстояния между кластерами
Метод одиночной связи	Метод полной связи
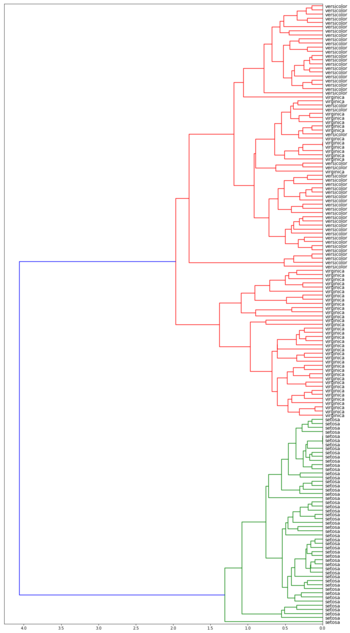
Метод средней связи	Метод Уорда

Лучше всего с задачей справился алгоритм с использованием расстояния Уорда. Он точно выделил класс Iris setosa и заметно отделили вид Iris virginica от Iris versicolor.

См. также

• Оценка качества в задаче кластеризации^{[на 14.12.18 не создан]}
• EM-алгоритм^{[на 14.12.18 не создан]}

Источники информации

• Википедия — Кластерный анализ
• Wikipedia — Cluster analysis
• MachineLearning — Кластеризация
• Википедия — Иерархическая кластеризация
• Scipy Documentation — Hierarchical clustering (scipy.cluster.hierarchy)
• К.В.Воронцов Лекции по алгоритмам кластеризации и многомерного шкалирования
• G. N. Lance, W. T. Williams; A General Theory of Classificatory Sorting Strategies: 1. Hierarchical Systems, The Computer Journal, Volume 9, Issue 4, 1 February 1967, Pages 373–380