Обратное распространение ошибки

Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.

Обучение как задача оптимизации

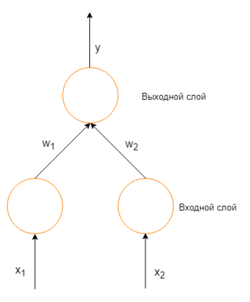
Чтобы понять математическое предназначение метода, требуется осознать взаимоотношения между действительными выходными значениями сети и требуемыми выходными значениями для конкретного примера из обучения. Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, которая является взвешенной суммой входных данных.

Простая нейронная сеть с двумя входными вершинами и одной выходной

Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек [math](x_1, x_2, t)[/math] где [math]x_1[/math] и [math]x_2[/math] — это входные данные сети и [math]t[/math] — правильный ответ. Начальная сеть, приняв на вход [math]x_1[/math] и [math]x_2[/math], вычислит ответ [math]y[/math], который вероятно отличается от [math]t[/math]. Общепринятый метод вычисления несоответствия между ожидаемым [math]t[/math] и получившимся [math]y[/math] ответом — квадратичная функция потерь:

[math]E=(t-y)^2, [/math] где [math]E[/math] ошибка.

В качестве примера, рассмотрим сеть с одним тренировочным объектом: [math](1, 1, 0)[/math], таким образом, значения [math]x_1[/math] и [math]x_2[/math] равны 1, а [math]t[/math] равно 0. Теперь, если действительный ответ [math]y[/math] изобразить на графике на горизонтальной оси, а ошибку [math]E[/math] на вертикальной, результатом будет парабола. Минимум параболы соответствует ответу [math]y[/math], который минимизирует ошибку [math]E[/math]. Для одиночного тренировочного объекта, минимум также касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ [math]y[/math] который точно соответствует ожидаемому ответу [math]t[/math]. Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.

График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом

В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:

[math]y=x_1w_1 + x_2w_2,[/math]

где [math]w_1[/math] и [math]w_2[/math] — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого "крутого" направления для спуска.

Дифференцирование для однослойной сети

Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, тогда квадратичная функция ошибки:

[math]E = \tfrac 1 2 (t - y)^2,[/math] где [math]E[/math] — квадратичная ошибка, [math]t[/math] — требуемый ответ для обучающего образца, [math]y[/math] — действительный ответ сети.

Множитель [math]\textstyle\frac{1}{2}[/math] добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. Позже, выражение будет умножено на произвольную величину скорости обучения, так что не имеет значения на какую константу мы умножим сейчас.

Для каждого нейрона [math]j[/math], его выходное значение [math]o_j[/math] определено как

[math]o_j = \varphi(\text{net}_j) = \varphi\left(\sum_{k=1}^n w_{kj}o_k\right).[/math]

Входные значения [math]\text{net}_j[/math] нейрона — это взвешенная сумма выходных значений [math]o_k[/math] предыдущих нейронов. Если нейрон в первом слове после входного слоя, то [math]o_k[/math] входного слоя — это просто входные значения [math]x_k[/math] сети. Количество входных значений нейрона [math]n[/math]. Переменная [math]w_{kj}[/math] обозначает вес на ребре между нейроном [math]k[/math] предыдущего слоя и нейроном [math]j[/math] текущего слоя.

Функция активации [math]\varphi[/math] нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:

[math] \varphi(z) = \frac 1 {1+e^{-z}}[/math]

у нее удобная производная:

[math] \frac {d \varphi(z)}{d z} = \varphi(z)(1-\varphi(z)) [/math]

Находим производную ошибки

Вычисление частной производной ошибки по весам [math]w_{ij}[/math] выполняется с помощью цепного правила:

[math]\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial o_j} \frac{\partial o_j}{\partial\text{net}_j} \frac{\partial \text{net}_j}{\partial w_{ij}}[/math]

Только одно слагаемое в [math]\text{net}_j[/math] зависит от [math]w_{ij}[/math], так что

[math]\frac{\partial \text{net}_j}{\partial w_{ij}} = \frac{\partial}{\partial w_{ij}} \left(\sum_{k=1}^n w_{kj} o_k\right) = \frac{\partial}{\partial w_{ij}} w_{ij} o_i= o_i.[/math]

Если нейрон в первом слое после входного, то [math]o_i[/math] — это просто [math]x_i[/math].

Производная выходного значения нейрона [math]j[/math] по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):

[math]\frac{\partial o_j}{\partial\text{net}_j} = \frac {\partial}{\partial \text{net}_j} \varphi(\text{net}_j) = \varphi(\text{net}_j)(1-\varphi(\text{net}_j))[/math]

По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)

Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае [math]o_j = y[/math] и

[math]\frac{\partial E}{\partial o_j} = \frac{\partial E}{\partial y} = \frac{\partial}{\partial y} \frac{1}{2}(t - y)^2 = y - t [/math]

Тем не менее, если [math]j[/math] произвольный внутренний слой сети, нахождение производной [math]E[/math] по [math]o_j[/math] менее очевидно.

Если рассмотреть [math]E[/math] как функцию, берущую на вход все нейроны [math]L = {u, v, \dots, w}[/math] получающие на вход значение нейрона [math]j[/math],

[math]\frac{\partial E(o_j)}{\partial o_j} = \frac{\partial E(\mathrm{net}_u, \text{net}_v, \dots, \mathrm{net}_w)}{\partial o_j}[/math]

и взять полную производную по [math]o_j[/math], то получим рекурсивное выражение для производной:

[math]\frac{\partial E}{\partial o_j} = \sum_{\ell \in L} \left(\frac{\partial E}{\partial \text{net}_\ell}\frac{\partial \text{net}_\ell}{\partial o_j}\right) = \sum_{\ell \in L} \left(\frac{\partial E}{\partial o_\ell}\frac{\partial o_\ell}{\partial \text{net}_\ell}w_{j\ell}\right)[/math]

Следовательно, производная по [math]o_j[/math] может быть вычислена если все все производные по выходным значениям [math]o_\ell[/math] следующего слоя известны.

Если собрать все месте:

[math] \frac{\partial E}{\partial w_{ij}} = \delta_j o_i [/math]

и

[math]\delta_j = \frac{\partial E}{\partial o_j} \frac{\partial o_j}{\partial\text{net}_j} = \begin{cases} (o_j-t_j)o_j(1-o_{j}) & \text{если } j \text{ является нейроном выходного слоя,}\\ (\sum_{\ell\in L} w_{j\ell} \delta_\ell)o_j(1-o_j) & \text{если } j \text{ является нейроном внутреннего слоя.} \end{cases}[/math]

Чтобы обновить вес [math]w_{ij}[/math] используя градиентный спуск, нужно выбрать скорость обучения, [math]\eta \gt 0[/math]. Изменение в весах должно отражать влияние [math]E[/math] на увеличение или уменьшение в [math]w_{ij}[/math]. Если [math]\frac{\partial E}{\partial w_{ij}} \gt 0[/math], увеличение [math]w_{ij}[/math] увеличивает [math]E[/math]; наоборот, если [math]\frac{\partial E}{\partial w_{ij}} \lt 0[/math], увеличение [math]w_{ij}[/math] уменьшает [math]E[/math]. Новый [math]\Delta w_{ij}[/math] добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на [math]-1[/math] гарантирует что [math]w_{ij}[/math] изменения будут всегда уменьшать [math]E[/math]. Другими словами, в следующем уравнении, [math]- \eta \frac{\partial E}{\partial w_{ij}}[/math] всегда изменяет [math]w_{ij}[/math] в такую сторону, что [math]E[/math] уменьшается:

[math] \Delta w_{ij} = - \eta \frac{\partial E}{\partial w_{ij}} = - \eta \delta_j o_i[/math]

Недостатки алгоритма

Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.

Градиентный спуск может найти локальный минимум вместо глобального

Паралич сети

В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.

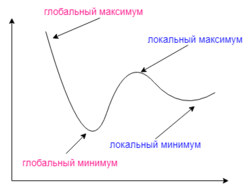
Локальные минимумы

Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.

Алгоритм

Алгоритм: BackPropagation [math](\eta, \alpha, \{x_i^d, t^d\}_{i=1,d=1}^{n,m}, \textrm{steps})[/math]

1. Инициализировать [math]\{w_{ij}\}_{i,j} [/math] маленькими случайными значениями, [math]\{\Delta w_{ij}\}_{i,j} = 0[/math]
2. Повторить [math]steps[/math] раз:

   .Для всех d от 1 до m:

   1. Подать [math]\{x_i^d\}[/math] на вход сети и подсчитать выходы [math]o_i[/math] каждого узла.
   2. Для всех [math]k \in Outputs[/math]

      [math]\delta _k = o_k(1 - o_k)(t_k - o_k)[/math].

   3. Для каждого уровня l, начиная с предпоследнего:

      Для каждого узла j уровня l вычислить

      [math]\delta _j = o_j(1 - o_j)\sum_{k \in Children(j)} \delta _k w_{j,k}[/math].

   4. Для каждого ребра сети {i, j}

      [math]\Delta w_{i,j}(n) = \alpha \Delta w_{i,j}(n-1) + ( 1 - \alpha ) \eta \delta _j o_{i}[/math].

      [math]w_{i,j}(n) = w_{i,j}(n-1) + \Delta w_{i,j}(n)[/math].

3. Выдать значения [math]w_{ij}[/math].

где [math]\alpha[/math] — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции

См. также

• Нейронные_сети,_перцептрон
• Стохастический градиентный спуск

Источники информации

• https://en.wikipedia.org/wiki/Backpropagation
• https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки