EM-алгоритм
Содержание
Определение
Алгоритм EM - алгоритм поиска максимума правдоподобия параметров для решения задач, где некоторые переменные не являются наблюдаемыми.
Алгоритм ищет параметры модели итеративно, каждая итерация состоит из двух шагов:
E(Expectation) шаг, в котором находится распределение скрытых переменных используя значение наблюдаемых переменных и текущего значения параметров.
M(Maximisation) шаг - пересчет параметров, находя максимум правдоподобия исходя из распределения скрытых переменных, полученных на E - шаге.
Задача разделения смеси распределений
Общий алгоритм
Необходимо описать плотность распределения функции на X как сумму k функций, которые можно рассматривать как элементы параметрического семейства функций . Плотность распределения будет выглядеть как
где - априорная вероятность j компоненты распределения.
Задача разделения смеси заключается в том, чтобы, имея выборку случайных и независимых наблюдений из смеси , зная число и функцию , оценить вектор параметров
E-шаг:
Введем обозначение: это и будут скрытые параметры данной задачи - апостериорная вероятность того, что обучающий объект получен из -й компоненты
По формуле Байеса справедливо равенство:
Таким образом при зная значение параметров легко найти скрытые переменные.
Перейдем к M-шагу:
Посчитаем для аддитивности логарифм правдоподобия:
при условии имеет смысл рассматривать лагранжиан задачи:
Умножим на и просумируем уравнения для всех
Так как можно заменить порядок суммы и и из чего следует
Приравняв к нулю лагранжиан по схожим способом найдем:
Таким образом на M-шаге необходимо взять среднее значение и решить k независимых оптимизационных задач.
Разделение смеси гауссиан
Важным на практике примером является случай, когда параметрическое семейство - нормальные распределения. Параметрами функций будут являться матожидание и дисперсия.
— вектор параметров,
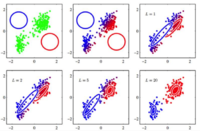
k-means как EM алгоритм
Скрытыми переменными в данной задаче являются классы, к которым относятся объекты для кластеризации. Сами же параметры это центры масс классов. На шаге E - распределяются все объекты по классам исходя из расстояния от центра, на шаге M находится оптимальное месторасположение центра.
Аналогично рассматривается и алгоритм c-means. Скрытые переменные здесь будут вероятности принадлежности к классам, которые находятся на E-шаге по расстоянию от центра. Центр так же рассчитывается на M-шаге исходя из скрытых переменных.