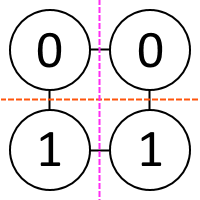
Невозможность византийского консенсуса
Можно доказать, например, что при n = 3, f = 1 (три процесса, из них один византийский) консенсус византийских генералов невозможен.
Доказательство от Елизарова:
Пусть каждому процессу подаётся число 0 или 1 на вход (могут быть разными на разных процессах). Задача - прийти к нетривиальному обоснованному консенсусу всем работающим процессам на одном значении, которое было дано на вход хотя бы одному невизантийскому процессу.
Предположим обратное. Пусть существует алгоритм консенсуса. Тогда расставим 4 ноды с этим алгоритмом, подадим верхним на вход 0, и нижним = 1.Тогда если считать 2 верхних процесса рабочими, а 2 нижних - одним сбойным, верхние обязаны прийти к консенсусу на 0. Аналогично, если считать 2 нижних процесса рабочими, а 2 верхних - одним сбойным - нижние приходят к консенсусу на 1.
И если мы считаем рабочими 2 правых, а 2 левых - одним сбойным(ведущим себя как пара из верхнего рабочего и нижнего рабочего) - то верхний правый придет к консенсусу на 0 вместе с воображаемым верхним соседом, а нижний правый - к консенсусу на 1 с воображаемым нижним соседом. Fail.
Поэтому такого алгоритма нет, и консенсус при N=3 и f=1 невозможен.