Персистентная очередь
Персистентная очередь (англ. persistent queue) — это очередь, реализующая персистентность, то есть позволяющая получить доступ ко всем своим предыдущим версиям. Как будет показано далее, можно реализовать функциональную персистентность, то есть каждая ячейка памяти в такой структуре будет инициализирована один раз и в дальнейшем не изменится.
Содержание
Основная идея
Для создания персистентной очереди очень удобно пользоваться ее реализацией на стеках, поскольку стеки легко сделать персистентными, причем в этом случае мы добьемся функциональной персистентности. Реализация на двух стеках не подходит для этого, так как в худшем случае требует времени, а значит и памяти на операцию в случае персистентности. Покажем сначала, как создать очередь в реальном времени с времени на операцию, а затем превратим ее в персистентную.
Реализация очереди на шести стеках
Одним из минусов реализации на двух стеках является то, что в худшем случае мы тратим времени на операцию. Если распределить время, необходимое для перемещения элементов из одного стека в другой, по операциям, мы получим очередь без худших случаев с истинного времени на операцию.
Сначала будем действовать аналогично случаю с двумя стеками. Пусть у нас есть стек для операций и стек для операций . К моменту опустошения стека нам нужно успеть получить стек , содержащий текущие элементы стека в правильном для извлечения порядке. Перекопирование (recopy mode) начнется, когда появится опасность того, что мы не сможем за оставшиеся операций со стеком перекопировать стек в новый стек . Очевидно, это ситуация , пусть такое состояние отражает специальная переменная логического типа .
Понятно, что во время перекопирования могут поступить операции , а стек в это время потеряет свою структуру, сложить элементы туда мы уже не сможем, значит нужно завести еще один стек , в который мы и будем складывать новые элементы. После окончания перекопирования мы поменяем ролями и , на первый взгляд, все станет хорошо.
Однако, если реализовать этот алгоритм, мы получим неприятную вещь: старый стек может и не опустошиться за это время, то есть мы получили два стека с выходными данными, а значит, возможен случай (например, если все поступающие операции — ), когда при следующем перекопировании у нас не будет свободного стека для копирования туда элементов . Для преодоления этой проблемы мы принудительно будем извлекать все элементы из стека во вспомогательный стек , затем копировать элементы из стека в , а затем обратно копировать элементы из стека в . Легко показать, что приведенный алгоритм как раз получает на выходе в все элементы стеков в правильном порядке.
Но этого еще недостаточно. Если мы принудительно извлекаем элементы из стека , появляются следующие проблемы:
- Что вернуть при операции ? Для этого заведем себе стек — копию стека , из которого мы и будем извлекать требуемые элементы.
- Как поддерживать корректность такой копии? Поскольку этот стек нужен только для перекопирования, а во время него он занят, нужна запасная копия для копирования всех элементов, которые мы копируем в , а по окончании перекопирования поменяем ролями стеки , как мы делали со стеками .
- Как учесть, что во время перекопирования часть элементов была извлечена из ? Для этого заведем специальную переменную , которая показывает, сколько корректных элементов находится в стеке , и уменьшается при каждом извлечении из или операции . К счастью, все некорректные элементы будут нарастать со дна стека, так что мы никогда не извлечем некорректный элемент, если . Если во время операции у нас , это означает, что теперь в стеке находится весь правый кусок очереди, так что нам придется извлечь элемент из него.
Теперь может возникнуть проблема с непустым после завершения перекопирования. Покажем, что мы всегда успеем его опустошить, если будем использовать дополнительное извлечение из него при каждой операции в обычном режиме, для этого полностью проанализируем алгоритм.
Пусть на начало перекопирования в стеке содержится элементов, тогда в стеке находится элементов. Мы корректно можем обработать любое количество операций , а также операций . Заметим, что операция во время перекопирования всегда возвращает , так как мы не можем извлекать элементы из стека , который не пустой. Таким образом вместе с операцией, активирующей перекопирование, мы гарантированно можем корректно обработать операцию.
Посмотрим на дополнительные действия, которые нам предстоят:
- Переместить содержимое в , действий.
- Переместить содержимое в стеки , действий.
- Переместить первые элементов из в , остальные выкинуть, действий.
- Поменять ролями стеки , , действия.
Таким образом, получили дополнительных действия за операций, или дополнительных действий на операцию в режиме перекопирования, что и требовалось.
Теперь рассмотрим, как изменились наши стеки за весь период перекопирования. Договоримся, что операция не меняет очередь, то есть никакие дополнительные действия не совершаются. Пусть за следующих за активацией меняющих операций () поступило операций , операций . Очевидно, что после перекопирования в новых стеках окажется: элементов в , элементов в , то есть до следующего перекопирования еще операции. С другой стороны, стек содержал всего элементов, так что мы можем очистить его, просто удаляя по одному элементу при каждой операции в обычном режиме.
Итак, очередь будет состоять из шести стеков , а также двух внутренних переменных , которые нужны для корректности перекопирования + дополнительная переменная , показывающая, перемещали ли мы элементы из стека в стек , чтобы не начать перемещать эти элементы в стек .
Инвариант очереди (обычный режим):
- Стек содержит левую половину очереди, порядок при извлечении обратный.
- Стек содержит правую половину очереди, порядок при извлечении прямой.
- — копия
Тогда к следующему перекопированию () мы гарантированно будем иметь пустые стеки , которые нам понадобятся.
Инвариант очереди (режим перекопирования):
- Если , то:
- При первые элементов — корректны, то есть действительно содержатся в очереди.
- При стек содержит весь правый кусок очереди в правильном порядке.
Очередь будет работать в двух режимах:
- Обычный режим, кладем в , извлекаем из и из для поддержания порядка, операция .
- Режим перекопирования, кладем в , извлекаем из , возможно из , , совершаем дополнительные действия.
Также после операции в обычном режиме следует проверка на активацию перекопирования (), если это так, , совершается первый набор дополнительных действий.
После операции в режиме перекопирования следует проверка на завершение перекопирования (), а при завершении меняются ролями стеки , .
Следующий псевдокод выполняет требуемые операции:
empty
boolean empty(): return !recopy and R.size == 0
push
function push(x : T):
if !recopy
L.push(x)
if Rc'.size > 0
Rc'.pop()
checkRecopy()
else
L'.push(x)
checkNormal()
pop
T pop():
if !recopy
T tmp = R.pop()
Rc.pop()
if Rc'.size > 0
Rc'.pop()
checkRecopy()
return tmp
else
T tmp = Rc.pop()
if toCopy > 0
toCopy = toCopy - 1
else
R.pop()
Rc'.pop()
checkNormal()
return tmp
checkRecopy
function checkRecopy():
recopy = L.size > R.size
if recopy
toCopy = R.size
copied = false
checkNormal()
checkNormal
function checkNormal():
additionalOperations()
// Если мы не все перекопировали, то у нас не пуст стек S
recopy = S.size 0
additionalOperations
function additionalOperations(): // Нам достаточно 3 операций на вызов int toDo = 3 // Пытаемся перекопировать R в S while not copied and toDo > 0 and R.size > 0 S.push(R.pop()) toDo = toDo - 1 // Пытаемся перекопировать L в R и Rc' while toDo > 0 and L.size > 0 copied = true T x = L.pop() R.push(x) Rc'.push(x) toDo = toDo - 1 // Пытаемся перекопировать S в R и Rc' с учетом toCopy while toDo > 0 and S.size > 0 T x = S.pop() if toCopy > 0 R.push(x) Rc'.push(x) toCopy = toCopy - 1 toDo = toDo - 1 // Если все скопировано, то меняем роли L, L' и Rc, Rc' if S.size == 0 swap(L, L') swap(Rc, Rc')
Персистентная очередь на пяти стеках
После того, как мы получили очередь в реальном времени с обычными стеками, ее можно легко превратить в персистентную, сделав все стеки персистентными, но на самом деле персистентность позволяет не создавать явной копии стека , так что достаточно всего пяти стеков.
Вместо стеков персистентная очередь хранит один стек , в который при активации перекопирования записывается последняя версия стека , в дальнейшем все операции обращаются именно к ней. Все замечания о остаются в силе.
Также нам нет необходимости опустошать стек к моменту перекопирования, так как скопировать туда новую версию мы можем за , а освобождение ячеек памяти бессмысленно, так как они используются в других версиях персистентной очереди.
В качестве версии очереди мы будем использовать запись , содержащую пять версий персистентных стеков и три переменных.
Пусть персистентный стек возвращает вместе с обычным результатом работы стека новую версию, то есть операция возвращает , а операция возвращает .
Аналогично свою новую версию вместе с результатом операции возвращает и персистентная очередь, то есть возвращает , а возвращает .
Следующий псевдокод выполняет требуемые операции:
empty
boolean empty(): return !recopy and R.size == 0
push
function push(x : T):
if !recopy
stack<T> Ln = L.push(x)
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> Q' = <Ln, L', R, R', S, recopy, toCopy, copied>
return Q'.checkRecopy()
else
stack<T> Ln' = L'.push(x)
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> Q' = <L, Ln', R, R', S, recopy, toCopy, copied>
return Q'.checkNormal()
pop
<stack<T>, T> pop():
if !recopy
<Rn, x> = R.pop()
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> Q' = <L, L', Rn, R', S, recopy, toCopy, copied>
return <Q'.checkRecopy(), x>
else
<Rn', x> = R'.pop()
int curCopy = toCopy
Rn = R
if toCopy > 0
curCopy = curCopy - 1
else
<Rn, x> = Rn.pop()
Q' = <L, L', Rn, Rn', S, recopy, curCopy, copied>
return <Q'.checkNormal(), x>
checkRecopy
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> checkRecopy():
if L.size > R.size
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> Q' = <L, L', R, R', S, true, R.size, false>
return Q'.checkNormal()
else
return <L, L', R, R', S, false, toCopy, copied>
checkNormal
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> checkNormal(): Q' = Q.additionalOperations() // Если мы не все перекопировали, то у нас не пуст стек S return <Q'.L, Q'.L', Q'.R, Q'.R', Q'.S, Q'.S.size 0, Q'.toCopy, Q'.copied>
additionalOperations
<stack<T>, stack<T>, stack<T>, stack<T>, stack<T>, boolean, int, boolean> additionalOperations(): // Нам достаточно 3 операций на вызов int toDo = 3 // Пытаемся перекопировать R в S stack<T> Rn = R stack<T> Sn = S boolean curCopied = copied while not curCopied and toDo > 0 and Rn.size > 0 <Rn, x> = Rn.pop() Sn = Sn.push(x) toDo = toDo - 1 Ln = L // Пытаемся перекопировать L в R while toDo > 0 and Ln.size > 0 curCopied = true <Ln, x> = Ln.pop() Rn = Rn.push(x) toDo = toDo - 1 curCopy = toCopy // Пытаемся перекопировать S в R с учетом toCopy while toDo > 0 and Sn.size > 0 <Sn, x> = Sn.pop() if curCopy > 0 Rn = Rn.push(x) curCopy = curCopy - 1 toDo = toDo - 1 stack<T> Ln' = L' // Если все скопировано, то меняем роли L1, L2 if S.size == 0 swap(Ln, Ln') return <Ln, Ln', Rn, R', Sn, recopy, curCopy, curCopied>
Пример
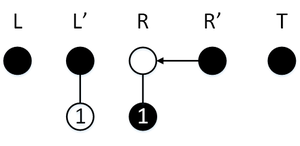
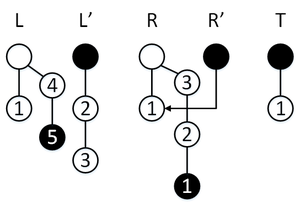
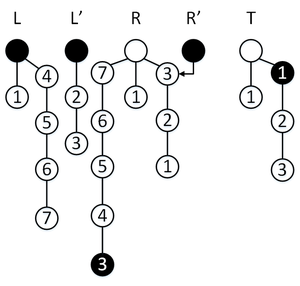
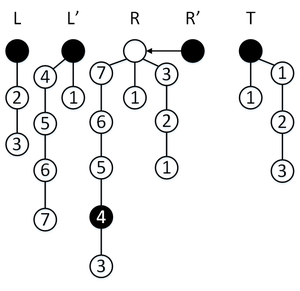
Пусть мы создали персистентную очередь. Будем изображать ее в виде пяти деревьев версий персистентных стеков, закрашенные вершины — текущие версии стеков, соответствующие текущему состоянию очереди; стрелка от стека указывает на ту версию стека , которая там сейчас хранится. В самих вершинах записаны соответствующие этим вершинам значения.
Сделаем операцию , изначально режим обычный, так что элемент пойдет в стек . Эта операция активирует режим перекопирования, в результате которого содержимое перекопируется в стек , после чего перекопирование завершится, стеки поменяются местами.
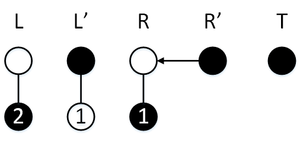
Сделаем операцию , у нас обычный режим, поэтому элемент пойдет в стек , перекопирование не активируется.
Сделаем операцию , у нас обычный режим, поэтому элемент пойдет в стек , активируется перекопирование, , за три операции мы успеваем перекопировать элемент стека в стек , а также перекопировать два элемента стека в стек .
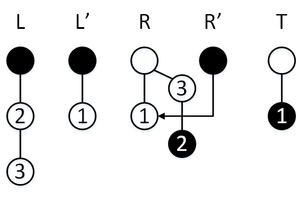
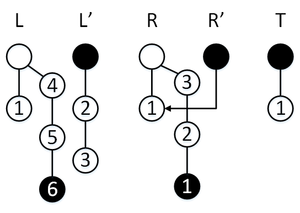
Сделаем операцию , мы в режиме перекопирования, поэтому элемент пойдет в стек , далее мы успеваем перекопировать обратно элемент из стека в стек , перекопирование завершается, стеки меняются местами.
Сделаем операцию , у нас обычный режим, поэтому элемент пойдет в стек , перекопирование не активируется.
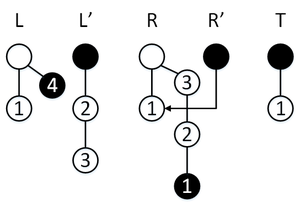
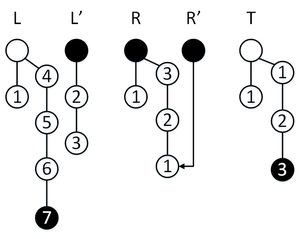
Сделаем операцию , у нас обычный режим, поэтому элемент пойдет в стек , перекопирование не активируется.
Сделаем операцию , у нас обычный режим, поэтому элемент пойдет в стек , перекопирование активируется, , , за три операции мы успеваем перекопировать содержимое стека в стек .
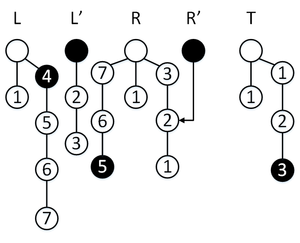
Сделаем операцию , мы находимся в режиме перекопирования, так что элемент извлекается из , . За три операции мы успеваем перекопировать три элемента стека в стек .
Сделаем операцию , мы находимся в режиме перекопирования, так что элемент извлекается из , . За три операции мы успеваем перекопировать один элемент стека в стек , а также извлечь два элемента стека , с учетом только один элемент попадет в стек , .
Сделаем операцию , мы находимся в режиме перекопирования, так что элемент извлекается из , но , так что нам приходится извлечь еше один элемент из стека . Мы извлекаем один элемент из стека , перекопирование заканчивается, стеки меняются местами.