Практики реализации нейронных сетей

Аугментация данных

При глубоком обучении иногда можно столкнуться с ситуацией, когда датасет имеет ограниченный размер. Но чтобы получить лучшее обобщение модели, необходимо иметь больше данных, в том числе и различные их вариации. То есть необходимо увеличить размер датасета искусственным образом, и это можно сделать с помощью аугментации данных.

Определение:

Аугментация данных (англ. data augmentation) — это методика создания дополнительных данных из имеющихся данных.

Чаще всего, проблема ограниченного датасета возникает при решении задач, связанных с обработкой изображений. Следующие способы аугментации изображений являются самыми популярными:

Рис 1. Пример аугментации изображения

• Отображение по вертикали или горизонтали (flipping).
• Поворот изображения на определенный угол (rotation).
• Создание отступа (padding).
• Вырезание части изображения (cropping).
• Добавление шума (adding noise).
• Манипуляции с цветом (color jittering).

Также, можно применять различные комбинации, к примеру, вырезать часть изображения, повернуть его и изменить цвет фона.

Продвинутыми способами аугментации данных является семейство GANs.

Дропаут

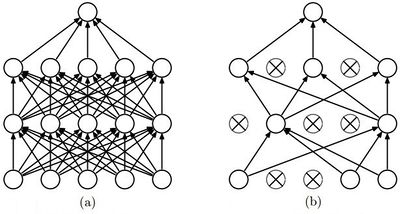
Одной из проблем глубокого обучения нейронных сетей является переобучение. И дропаут значится как один из самых популярных способов устранения этой проблемы, благодаря своей простоте и хорошим практическим результатам.

Определение:

Дропаут (англ. dropout) — метод регуляризации нейронной сети для предотвращения переобучения.

В обычной нейронной сети явление переобучения появляется из-за так называемой совместной адаптации (англ. co-adaptation), то есть при обновлении весов нейрона, во время обучения методом обратного распространения ошибки, учитывается деятельность остальных нейронов с целью минимизировать функцию потерь. Поэтому веса нейронов могут меняться, исправляя при этом ошибки других нейронов. Метод дропаута как раз предотвращает эту адаптацию.

Рис 2. Пример применения метода дропаут

Как работает дропаут

Рассмотрим слой нейронной сети состоящий из [math]H[/math] нейронов. Метод дропаут выключает нейрон с вероятностью [math]p[/math], соответственно, оставляет включенным с вероятностью [math]q = 1 - p[/math], причем вероятность выключения любого нейрона сети одинакова.

Пусть [math]a(x)[/math] — функция активации, тогда применение дропаута для [math]i[/math]-ого нейрона выглядит так: [math]U_{i} = \Theta_{i}a(\sum\limits^{H}_{k=1} w_{k}x_{k} + b)[/math],

где вероятность [math]P(\Theta_{i}[/math][math]=[/math][math]0)[/math] [math]= p[/math].

Данная формула применяется на этапе обучения модели. Но так как на этом этапе нейрон остается в сети с вероятностью [math]q[/math], на этапе тестирования необходимо эмулировать поведение нейронной сети, использованного при обучении. Для этого результат выходного значения функции активации умножается на коэффициент [math]q[/math], то есть на этапе тестирования: [math]U_{i} = qa(\sum\limits^{H}_{k=1} w_{k}x_{k} + b)[/math].

Обратный дропаут

Обратный дропаут (англ. inverted dropout) отличается от обычного тем, что умножение на коэффициент происходит на этапе обучения, причем этот коэффициент равен обратной вероятности того, что нейрон останется в сети: [math]\dfrac1{q}[/math]. А на этапе тестирования выходное значение нейрона остается таким же, как и в методе обратного распространения ошибки.

Таким образом, выходное значение [math]i[/math]-ого нейрона на этапе обучения: [math]U_{i} = \dfrac1{q}\Theta_{i}a(\sum\limits^{H}_{k=1} w_{k}x_{k} + b)[/math], на этапе тестирования: [math]U_{i} = a(\sum\limits^{H}_{k=1} w_{k}x_{k} + b)[/math].

Обратная модификация дропаута на практике используется чаще обычной, потому что в ней не нужно менять каждый раз модель для проведения этапа тестирования.

Функции активации

Одним из важнейших аспектов глубокой нейронной сети являются функции активации.

Определение:

Функция активации (англ. activation function) определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения.

Рассмотрим нейрон [math]Z[/math] с выходным значением [math]Z = \sum\limits_{i} w_{i}x_{i} + bias[/math], где [math]w_{i}[/math] и [math]x_{i}[/math] — вес и входное значение [math]i[/math]-ого входа, а [math]bias[/math] — смещение. Полученный результат передается в функцию активации, которая решает рассматривать этот нейрон как активированный, или его можно игнорировать.

Рис 3. Ступенчатая функция

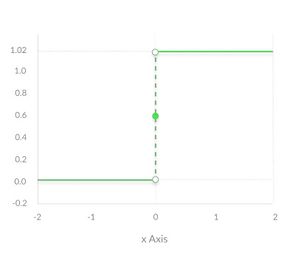
Ступенчатая функция

Ступенчатая функция (англ. binary step function) является пороговой функцией активации. То есть если [math]Z[/math] больше или меньше некоторого значения, то нейрон становится активированным. Такая функция отлично работает для бинарной классификации. Но она не работает, когда для классификации требуется большее число нейронов и количество возможных классов больше двух.

Рис 4. Линейная функция

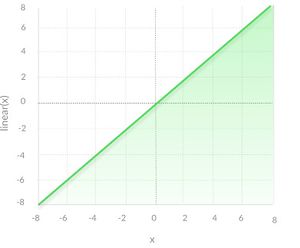
Линейная функция

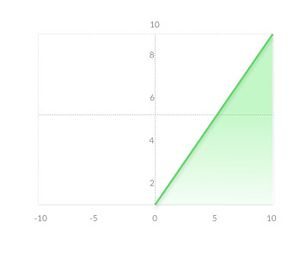
Линейная функция (англ. linear function) представляет собой прямую линию, то есть [math]Z = \sum\limits_{i} w_{i}x_{i}[/math], а это значит, что выходное значение этой функции активации пропорционально входному. В отличии от предыдущей функции, она позволяет получить диапазон значений на выходе, а не только бинарные 0 и 1, что решает проблему классификации с большим количеством классов. Но у линейной функции есть две основных проблемы:

1. Невозможность использования метода обратного распространения ошибки. Так как в основе этого метода обучения лежит градиентный спуск, а для того чтобы его найти, нужно взять производную, которая для данной функции активации — константа и не зависит от входных значений. То есть при обновлении весов нельзя сказать улучшается ли эмпирический риск на текущем шаге или нет.
2. Рассмотрим нейронную сеть с несколькими слоями с данной функцией активации. Так как для каждого слоя выходное значение линейно, то они образуют линейную комбинацию, результат которой является линейной функцией. То есть финальная функция активации на последнем слое зависит только от входных значений на первом слое. Это значит, что любое количество слоев может быть заменено всего одним слоем.

Рис 5. Сигмоидная функция

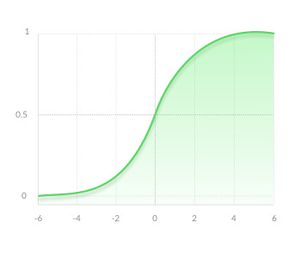
Сигмоидная функция

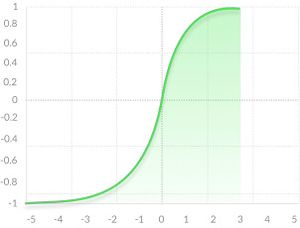
Сигмоидная функция (англ. sigmoid function), которую также называет логистической функцией (англ. logistic function), является гладкой монотонно возрастающей нелинейной функцией — [math]\sigma(z) = \dfrac1{1+e^{-z}}[/math]. И так как эта функция нелинейна, то ее можно использовать в нейронных сетях с множеством слоев, а также обучать эти сети методом обратного распространения ошибки. Сигмоида ограничена двумя горизонтальными асимптотами [math]y = 1[/math] и [math]y = 0[/math], что дает нормализацию выходного значения каждого нейрона. Кроме того, для сигмоидной функции характерен гладкий градиент, который предотвращает "прыжки" при подсчете выходного значения. У этой функции есть еще одно преимущество, для значений [math]x \gt 2[/math] и [math]x \lt -2[/math], [math]y[/math] "прижимается" к одной из асимптот, что позволяет делать четкие предсказания классов.

Несмотря на множество сильных сторон сигмоидной функции, у нее есть значительные недостатки. Производная такой функции крайне мала во всех точках, кроме сравнительно небольшого промежутка. Это сильно усложняет процесс улучшения весов с помощью градиентного спуска. Более того, эта проблема усугубляется в случае, если модель содержит много слоев. Данная проблема называется проблемой исчезающего градиента.

Рис 6. Функция гиперболического тангенса

Функция гиперболического тангенса

Функция гиперболического тангенса (англ. hyperbolic tangent) имеет вид — [math]tanh(z) = \dfrac2{1+e^{-2z}} - 1[/math]. Эта функция является скорректированной сигмоидной функцей [math]tanh(z) = 2 \cdot sigma(2z) - 1[/math], то есть она сохраняет те же преимущества и недостатки, но уже для диапазона значений [math](-1; 1)[/math].

Рис 7. Функция ReLU

Функция ReLU

Rectified Linear Unit — это наиболее часто используемая активационная функция при глубоком обучении. Данная функция возвращает 0, если принимает отрицательный вход, в случае же положительного входа, функция возвращает само число. То есть функция может быть записана как [math]f(z)=max(0, z)[/math]. На первый взгляд может показаться, что она линейна и имеет те же проблемы что и линейная функция, но это не так и ее можно использовать в нейронных сетях с множеством слоев. Функция ReLU обладает несколькими преимущества перед сигмоидой и гиперболическим тангенсом:

1. Очень просто считается производная. Для отрицательных значений — 0, для положительных — 1.
2. Разреженность активации. В сетях с очень большим количеством нейронов использование сигмоидной функции или гиперболического тангенса в качестве активационный функции влечет активацию почти всех нейронов, что может сказаться на производительности обучения модели. Если же использовать ReLU, то количество включаемых нейронов станет меньше, в силу характеристик функции, и сама сеть станет легче.

У данной функции есть один недостаток, называющийся "Проблемой умирающего ReLU" (Dying ReLu problem). Так как часть производной функции равна нулю, то и градиент для нее будет нулевым, а то это значит, что веса не будут изменяться во время спуска и нейронная сеть перестанет обучаться.