EM-алгоритм

Определение

Алгоритм EM (англ: expectation-maximization) --- итеративный алгоритм поиска оценок максимума правдоподобия модели, в ситуации, когда она зависит от скрытых(ненаблюдаемых) переменных.

Алгоритм ищет параметры модели итеративно, каждая итерация состоит из двух шагов:

E(Expectation) шаг --- поиск наиболее вероятных значений скрытых переменных.

M(Maximisation) шаг --- поиск наиболее вероятных значений параметров, для полученных на шаге E значений скрытых переменных.

EM алгоритм подходит для решения задач двух типов:

1. Задачи с неполными данными.
2. Задачи, в которых удобно вводить скрытые переменные для упрощения подсчета функции правдоподобия. Примером такой задачи может служить кластеризация

Проблема восстановления распределения смеси

Постановка задачи

Плотность распределения смеси имеет вид:
[math]p(x) = \sum\limits_{i=1}^k \omega_j p_j(x)[/math]
Где [math] \sum\limits_{i=1}^k w_j = 1; w_j \gt = 0; p_j(x) = \phi(x;\theta_j)[/math] - функция правдоподобия [math]j[/math]-ой компонеты смеси, [math]\omega_j[/math] - априорная вероятность [math]j[/math]-ой компоненты распределения.

Перед нами стоит две задачи:

1. По заданной выборке [math]X^m[/math] случайных и независимых наблюдений полученных из смеси [math]p(x)[/math], числу [math]k[/math] и функцию [math]\phi[/math], оценить вектор параметров [math]\Theta = (\omega_1,..,\omega_k,\theta_1,..,\theta_k)[/math]
2. Найти [math]k[/math]

Проблема

Задачи подобного рода мы умеем решать максимизируя логармиф правдоподобия:
[math] L(\Theta) = ln \prod\limits_{i=1}^mp(x_i) = \sum\limits_{i=1}^m ln\sum\limits_{j=1}^k w_j p_j(x_i; \theta_j) \longrightarrow max[/math]

Но пробелма в том, что мы не знаем как аналитически посчитать логарифм суммы. Тут нам и поможет алгоритм EM.

Решение

Основная идея алгоритма EM заключается в том, что мы добавляме скрытые переменные такие, что:

1. Они могут быть выражены через [math]\Theta[/math]
2. Они помогают разбить сумму так: [math]p (X, H|\Theta) = \prod\limits_{i=1}^k p (X|H, \Theta) p(H|\Theta)[/math], где [math]H[/math] - матрица скрытых переменных.

Тогда алгоритм EM сводится к повторению шагов, указанных в Определение.

E-шаг

[math]p(x,\theta_j) = p(x)P(\theta_j | x) = w_jp_j(x)[/math]

Скрытые переменные представляют из себя матрицу [math]H = (h_{ij})_{m \times k}[/math]
где [math]h_{ij} = P(\theta_j | x_i)[/math] - вероятность того, что [math]x_i[/math] пренадлежит [math]j[/math]-ой компоненте.

По формуле Байеса справедливо равенство:
[math] h_{ij} = \frac{w_jp_j(x_i)}{p (x_i)} = \frac{w_jp_j(x_i)}{\sum\limits_{s=1}^k w_s p_s(x_i)}[/math]

Также [math]\sum\limits_{j=1}^k h_{ij} = 1[/math]

Таким образом, зная значения вектора параметров [math]\Theta[/math], мы легко можем пересчитать значения скрытых переменных

M-шаг

Теорема:

Если известны скрытые переменные, то задача минимизации [math]Q(\Theta)[/math] сводится к [math]k[/math] независимым подзадачам: [math]\theta_j = argmax_{\theta} \sum\limits_{i=1}^m h_{ij}*ln \phi (x_i, \theta)[/math] Оптимальные же веса считаются как: [math] w_j = \frac {1} {m} \sum\limits_{i=1}^m h_{ij}[/math]

Псевдокод

Input:[math]X^m, k, \theta^{(0)}[/math]
Repeat
   E-step: for all i = 1..m; j = 1..k:
       [math]h_{ij} = \frac{w_jp_j(x_i)}{\sum\limits_{s=1}^k w_s p_s(x_i)}[/math]
   M-step: for all j = 1..k:
       [math]\theta_j = argmax_{\theta} \sum\limits_{i=1}^m h_{ij}*ln \phi (x_i, \theta)[/math]
       [math]w_j = \frac {1} {m} \sum\limits_{i=1}^m h_{ij}[/math]
Until stopping criteria is satisfied

Плюсы и минусы

Плюсы:

• Сходится в большинтсве ситуаций
• Наиболее гибкое решение
• Легко может добавить нечуствительность к шуму

Минусы:

• Чуствителен к начальному приближению. Могут быть ситуации, когда сойдемся к локальному экстремуму
• Число компонент [math]k[/math] является гиперпараметром.

Модификации

Базовый алгоритм EM является очень гибким для модификаций, позволяющих улучшить его работу. В этом разделе мы приведем краткое описаниен некоторых из них.

Generalized EM-algorithm

Осоновная идея этой модификации заключается в том, что на шаге M мы не будем пытаться найти наилучшее решение. Это применимо в случаях, когда максимизация [math]Q(\Theta)[/math] является сликшом дорогой, поэтому нам достаточно сделать лишь несколько итераций, для того, чтобы сместиться в сторону максимума значения [math]Q(\Theta)[/math]. Эта модификация имеет неплохую сходимость.

Stochastic EM-algorithm

Как уже было отмечено в Плюсы и минусы, базовый алгоритм чувствителен к начальному приближению и могут быть ситуации, когда алгоритм "застрянет" в лоакльном экстремуме. Для того, чтобы предотвратить это, будем на каждой итерации алгоритма случайно "встряхивать" выборку. В этой модификации у нас добавляется шаг S, на котором мы и будем "встряхивать" выборку. И на шаге M мы будем решать уже задачу максимуму невзвешенного правдоподобия. Эта модификация хороша тем, что нечуствиетльная к начальном приблежению.

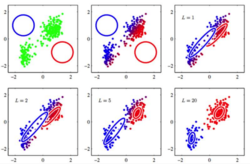
Пример. Разделение смеси Гауссиана

Каноническим примером использования EM алгоритма является задача разделения смеси гауссиана. Данные у нас получены из нормального распределения. В этом лучае параметрами функций ялвяются матожидание и дисперсия.

[math]\theta = (w_1,..,w_k;\;\mu_1,..,\mu_k;\;\sigma_1,..,\sigma_k)[/math] — вектор параметров,
[math]p_j(x) = N(x;\mu_j, \sigma_j) = \frac1{\sqrt{2\pi}\sigma_j} \exp \biggl(-\frac{(x - \mu_j)^2}{2\sigma_j^2}\biggr) [/math] - плотность распределения

Посчитаем значения для каждого шага.

E-шаг:

[math] h_{ij} = \frac{w_j N(x_i, \mu_j, \sigma_j)}{\sum\limits_{s=1}^k w_s N(x_i, \mu_s, \sigma_s)} [/math]

M-шаг:

[math]w_j = \frac{1}{m} \sum\limits_{i=1}^m h_{ij}[/math]

[math] \mu_j = \frac {1} {mw_j} \sum\limits_{i=1}^m h_{ij}x_i[/math]

[math] \sigma_j^2 = \frac {1} {mw_j} \sum\limits_{i=1}^m h_{ij}(x_i - \mu_j)^2, j = 1..k[/math]

Задача разделения смеси распределений

Общий алгоритм

Необходимо описать плотность распределения функции на X как сумму k функций, которые можно рассматривать как элементы параметрического семейства функций [math] p_j(x) = \phi(x;\theta_j)[/math]. Плотность распределения будет выглядеть как
[math]p(x) = \sum\limits_{i=1}^k \omega_j p_j(x); \sum\limits_{i=1}^k w_j = 1; w_j \gt = 0 [/math]
где [math]\omega_j[/math]- априорная вероятность j компоненты распределения. Задача разделения смеси заключается в том, чтобы, имея выборку [math]X^m[/math] случайных и независимых наблюдений из смеси [math]p(x)[/math], зная число [math]k[/math] и функцию [math]\phi[/math], оценить вектор параметров [math]\theta = (\omega_1,..,\omega_k,\theta_1,..,\theta_k)[/math]

E-шаг:

[math]p(x,\theta_j) = p(x)P(\theta_j | x) = w_jp_j(x)[/math]
Введем обозначение: [math] g_{ij} = P(\theta_j | x_i) [/math] это и будут скрытые параметры данной задачи - апостериорная вероятность того, что обучающий объект [math] x_i [/math] получен из [math]j[/math]-й компоненты

По формуле Байеса справедливо равенство:
[math] g_{ij} = \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^k w_t p_t(x_i)}[/math]
Таким образом при зная значение параметров легко найти скрытые переменные.

Перейдем к M-шагу.

Посчитаем для аддитивности логарифм правдоподобия:
[math] Q(\Theta) = ln \prod\limits_{i=1}^mp(x_i) = \sum\limits_{i=1}^m ln\sum\limits_{j=1}^k w_j p_j(x_i) \longrightarrow max[/math]
при условии [math]\sum\limits_{i=1}^k w_j = 1; w_j \gt = 0[/math] имеет смысл рассматривать лагранжиан задачи:
[math]\frac{\partial L} {\partial w_j} = \sum\limits_{i=1}^m \frac{p_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} - \lambda = 0.[/math]

Умножим на [math]\omega_j[/math] и просуммируем уравнения для всех [math]j[/math]

[math]\sum\limits_{j=1}^k \sum\limits_{i=1}^m \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = \lambda \sum\limits_{j=1}^kw_j[/math]

Так как можно заменить порядок суммы: [math] \sum\limits_{i=1}^m \sum\limits_{j=1}^k \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = \lambda \sum\limits_{j=1}^kw_j[/math].

А так как [math]\sum\limits_{j=1}^k \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = 1[/math] и [math]\sum\limits_{j=1}^kw_j = 1[/math], из чего следует [math]\lambda = m[/math]

[math]\omega_j = \frac{1}{m}\sum\limits_{i=1}^m \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = \frac{1}{m}\sum\limits_{i=1}^mg_{ij}[/math]

Приравняв к нулю лагранжиан по [math]\theta_j[/math] схожим способом найдем:

[math] \theta_j = \arg\max\limits{\theta}\sum\limits_{i=1}^mg_{ij}\ln(\phi(x_i;\theta)).[/math]

Таким образом на M-шаге необходимо взять среднее значение [math]g_{ij}[/math] и решить k независимых оптимизационных задач.

Разделение смеси гауссиан

Важным на практике примером является случай, когда параметрическое семейство - нормальные распределения. Параметрами функций будут являться матожидание и дисперсия.
[math]\theta = (w_1,..,w_k;\;\mu_1,..,\mu_k;\;\sigma_1,..,\sigma_k)[/math] — вектор параметров,
[math]p_j(x) = N(x;\mu_j, \sigma_j) = \frac1{\sqrt{2\pi}\sigma_j} \exp \biggl(-\frac{(x - \mu_j)^2}{2\sigma_j^2}\biggr) [/math]

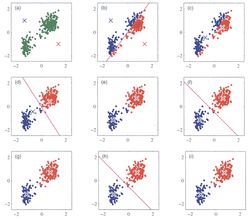
k-means как EM алгоритм

Скрытыми переменными в данной задаче являются классы, к которым относятся объекты для кластеризации. Сами же параметры это центры масс классов. На шаге E - распределяются все объекты по классам исходя из расстояния от центра, на шаге M находится оптимальное месторасположение центра.

Аналогично рассматривается и алгоритм c-means. Скрытые переменные здесь будут вероятности принадлежности к классам, которые находятся на E-шаге по расстоянию от центра. Центр так же рассчитывается на M-шаге исходя из скрытых переменных.

Реализация на python

import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets, mixture
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
np.random.seed(12)

# Создаем datasets с использованием стандартных sklearn.datasets
n_samples = 2000
random_state = 170
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
varied = datasets.make_blobs(n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state)

# Создаем анизатропно разделенные данные
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)

# Выставляем параметры для matplotlib.pyplot
plt.figure(figsize=(9 * 2 + 3, 12.5))
plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05, hspace=.01)
plot_num = 1
defaul_n = 3

# Варьируем значение количества классов в зависимости от данных, ведь для нас это гиперпараметр
datasets = [
   (varied, defaul_n),
   (aniso, defaul_n),
   (blobs, defaul_n),
   (noisy_circles, 2)]
for i_dataset, (dataset, n_cluster) in enumerate(datasets):
   X, y = dataset

   # Нормализация данных
   X = StandardScaler().fit_transform(X)

   # Непосредственно наш алгоритм - Gaussian Mixture
   gmm = mixture.GaussianMixture(n_components=n_cluster, covariance_type='full')
   
   # Для сравнения берем алгоритм - K-means
   two_means = cluster.KMeans(n_clusters=n_cluster)
   clustering_algorithms = (
       ('GaussianMixture', gmm),
       ('KMeans', two_means)
   )
   for name, algorithm in clustering_algorithms:

       # Этап обучения
       algorithm.fit(X)
       
       # Применяем алгоритм
       y_pred = algorithm.predict(X)
       
       # Рисуем результаты
       plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
       if i_dataset == 0:
           plt.title(name, size=18)
       colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a']), int(max(y_pred) + 1))))
       plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
       plt.xlim(-2.5, 2.5)
       plt.ylim(-2.5, 2.5)
       plt.xticks(())
       plt.yticks(())
       plot_num += 1
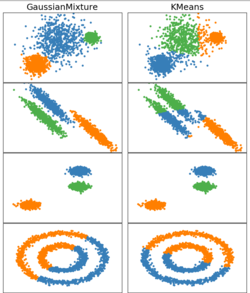
plt.show()

Результат программы

Как и следовало ожидать, алгоритм работает на некоторых данных лучше чем k-means, однако есть данные, с которыми он не справляется без дополнительных преобразований.

См. также

• Кластеризация

Источники информации

1. Математические методы обучения по прецедентам К. В. Воронцов
2. k-means