Представление знаний

Материал из Викиконспекты
Версия от 20:07, 7 января 2021; 109.111.77.104 (обсуждение) (→‎Извлечение термов и концептов)
Перейти к: навигация, поиск

Представление знаний (англ. knowledge representation) — направление в исследованиях искусственного интеллекта, посвящённое представлению информации о мире в форме, которую было бы возможно использовать в компьютерных системах для решения сложных задач, таких как диагностирование заболеваний или ведение диалога на естественном языке. Представление знаний включает в себя психологические исследования по решению задач человеком для построения формализмов, которые упростили бы работу со сложными системами. Примерами формализмов представления знаний являются семантические сети, архитектуры систем, правила и онтологии.

Графы знаний

История

Определение:
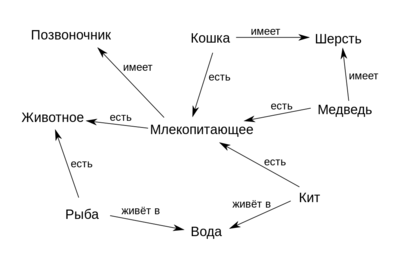
Семанти́ческая сеть [1] (англ. semantic network) — информационная модель предметной области, представленная в виде ориентированного графа. Вершины при этом соответствуют объектам предметной области, а рёбра представляют отношения между ними. Семантическая сеть — это один из способов представления знаний.
Пример семантической сети

Семантические сети были разработаны в 1960 году из-за растущей необходимости в инструменте для представления знаний, который мог бы охватить широкий спектр сущностей: объекты реального мира, события, ситуации и отвлечённые концепты и отношения, — в конце концов будучи применённым в задаче поддержания диалога на естественном языке. Основной целью разработки семантических сетей было решение множества задач, например, представление планов, действий, времени, верований и намерений. При этом способ решения этих задач должен был быть достаточно обобщённым.

В 1980-х гг. Гронингенский университет и университет Твенте начали работу над совместным проектом, названным "Графы знаний", базируясь на устройстве семантических сетей с рёбрами, ограниченными наперёд заданным количеством отношений — для упрощения алгебры на графах. В последовавшие десятилетия граница между понятиями "Графов знаний" и "Семантических сетей" размывалась всё больше.

В 2012 же году Google представили свою версию графа знаний.

Определение

Не существует формального определения графа знаний. Однако есть ряд аксиом, которым граф знаний должен удовлетворять [2].

  1. Значение графа знаний выражается в его структуре.
  2. Утверждения внутри графа знаний являются однозначными.
  3. Граф знаний использует конечный набор типов отношений.
  4. Все указанные сущности внутри графа знаний, включая типы и отношения, должны быть определены с использованием глобальных идентификаторов с однозначными обозначениями.
  5. Утверждения в графе знаний должны иметь явно указанные источники.
  6. Граф знаний может иметь оценки неопределённостей.

Применение

Вопросно-ответные системы. Самым распространённым применением графов знаний являются вопросно-ответные системы. Графы знаний располагают огромным количеством информации, доступ к которой проще всего получать посредством схемы вопрос-ответ.

Хранение информации исследований. Многие компании используют графы знаний для хранения результатов, полученных на разных стадиях исследований, которые могут быть использованы для построения понятных моделей, просчёта рисков, слежения за различными процессами и т. д.

Рекомендательные системы. Некоторые компании используют графы знаний как фундамент для своих рекомендательных систем. Здесь графы знаний позволяют находить связи между фильмами, телепрограммами, персоналиями и т. д. По выявленным связям можно пытаться предсказать индивидуальные предпочтения пользователя.

Управление цепочками поставок. Компании могут эффективно следить за перечнями различных составляющих, задействованного персонала, времени и др., что позволяет им передавать вещи более выгодно.

Открытые проблемы

  1. Выявление лучших практик для построения графов знаний.
  2. Динамически изменяемые знания.
  3. Оценка корректности и полноты графа знаний.

Онтология

Понятие онтологии существует как в информатике, так и в философии, однако эти понятия похожи.

Определение:
Онтология (в информатике) — формализация знаний, включающая в себя представление, формальное именование и определение категорий, свойств и отношений между понятиями, данными и сущностями некоторой области знаний.

Формализация

Для формализации используется концептуальная схема.

Определение:
Концептуа́льная схе́ма[3] — семантическая сеть из взаимосвязанных по определенным правилам понятий и концепций. Обычно такая схема состоит из структуры данных, содержащей все релевантные классы объектов, их связи и правила (теоремы, ограничения), принятые в этой области.

Философия

Термин «онтология» в информатике является производным от соответствующего древнего философского понятия.

Общее с философским понятием:

  • И то, и другое — попытка представить сущности, идеи и события со всеми их взаимозависимыми свойствами и отношениями в соответствии с системой категорий.
  • В обеих областях существует значительная работа по проблемам онтологической инженерии[4].

Отличия от философского понятия:

  • Онтология в информатике должна иметь формат, который компьютер сможет легко обработать.
  • Информационные онтологии создаются всегда с конкретными целями — решения конструкторских задач; они оцениваются больше с точки зрения применимости, чем полноты.

Каждая научная дисциплина или область знаний создает онтологии для ограничения сложности и организации данных в информацию и знания. Новые онтологии улучшают решение проблем в этой области. Перевод научных работ в каждой области — это проблема, облегченная, когда эксперты из разных стран поддерживают контролируемый словарь[5] жаргона между каждым из своих языков.

Элементы

Общие компоненты онтологий включают в себя:

  • Экземпляры (объекты) — базовые или "наземные" объекты.
  • Классы (понятия) — наборы, коллекции, концепции, классы в программировании, типы объектов или виды вещей.
  • Атрибуты — аспекты, свойства, признаки, характеристики или параметры, которые могут иметь объекты (и классы).
  • Отношения — способы, которыми классы и индивиды могут быть связаны друг с другом.
  • Термы функций — сложные структуры, образованные из определенных отношений, которые могут быть использованы вместо отдельного термина в высказывании.
  • Ограничения — формально заявленные описания того, что должно быть истинным для того, чтобы какое-то утверждение было принято в качестве входных данных.
  • Правила — высказывания в форме предложения if-then (антецедент-консеквент), описывающие логические выводы, которые могут быть сделаны из утверждения в определенной форме.
  • Аксиомы — утверждения (включая правила) в логической форме, которые вместе составляют общую теорию, которую онтология описывает в своей области применения. Это определение отличается от определения "аксиом" в порождающей грамматике и формальной логике. В этих дисциплинах аксиомы включают только утверждения, утверждаемые как априорное знание. Здесь же "аксиомы" также включают в себя теорию, полученную из аксиоматических утверждений.
  • События — изменение атрибутов или отношений.

Онтологии обычно кодируются с помощью языков онтологий — формальных языков, используемых для этой цели.

Примерами таковых являются OWL[6] , KIF[7] , Common Logic[8] , CycL[9] , DAML+OIL[10].

Построение при помощи методов машинного обучения

Векторные представления графов знаний

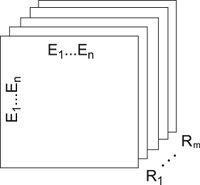
Тензорная модель представления графов знаний. [math]E_1 \dots E_n[/math] обозначают объкты, а [math]R_1 \dots R_m[/math] обозначают отношения

Для представления графовых данных используются семантика Cреды описания ресурса (англ. Resource Description Framework, RDF)[11] где связи представляются триплетом "субъект — предикат — объект". Для моделирования бинарных отношений на графе удобно использовать трехсторонний тензор [math]X[/math], в котором две размерности образованы на основе связываемых объектов-узлов, а третья размерность содержит отношения между ними (см. иллюстрацию). Элемент тензора [math]x_{ijk} = 1[/math], когда существует отношение (i-й объект, k-е отношение, j-й объект). В противном случае для несуществующих или неизвестных отношений [math]x_{ijk} = 0[/math].

Обучение онтологий

Слоеный пирог обучения онтологий

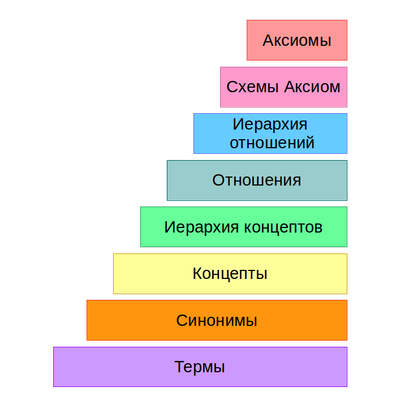
Процесс получения онтологий начинается с вынесения множества терминов из текста и получения их синонимов. Далее они преобразуются во множество концептов. После чего выявляются связи между концептами, и в итоге формируются схемы аксиом и извлекаются аксиомы. Данный процесс называют слоеным пирогом обучения онтологии.

Алгоритмы, используемые в разных слоях при построении онтологии разбивают на 3 основные группы:

  • Лингвистические
  • Статистические
  • Логические

Лингвистические методы

Лингвистические методы основаны на различных особеностях языка и играют ключевую роль практически на всех стадиях пирога обучения онтологий. В основном их используют для предобработки текста, а также в извлечении термов, концептов и связей.

Предобработка текста

На первой стадии текст предобрабатывается для уменьшения размерности и повышения точности обучаемой модели. Обычно для этого используют такие методы, как:

Извлечение термов и концептов

Лингвистические техники также часто используют на этапе извлечения термов и концептов. Чтобы извлечь термы и концепты при помощи синтаксических структур слова помечают как части речи. Эта информация используется для извлечения синтаксических структур из предложений, таких как словосочетания и глагольные группы. Данные структуры анализируются на наличие различных слов и морфем для нахождения термов. К примеру словосочетание ‘acute appendicitis’ может быть извлечено в качестве кандидата на терм, т.к. является гипонимом к терму ‘appendicitis’. На китайских текстах данный метод достиг точности в [math]83.3\%[/math].

Распространёнными методами данного подхода являются:

  • Рамки валентностей (англ. Subcategorization Frames)[14]
  • Извлечение ключевых слов

Статистические методы

Извлечение термов и концептов

На этом этапе используются следующие техники:

Нахождение связей

Помимо нахождения самих концептов необходимо найти связи между ними. Обычно для этого используют смесь обработки текстов на естественном языке и статистические подходы такие как:

Индуктивное логическое программирование

Определение:
Индуктивное логическое программирование[17] (англ. Inductive Logic Programming, ILP) — раздел машинного обучения, который использует логическое программирование как форму представления примеров, фоновых знаний и гипотез.

В онтологии ILP используется на последней стадии для генерации аксиом по схамам аксиом (полжительным и отрицательным примерам и фоновым знаниям).

Формирование онтологии

Для формировния целостной онтологии инпользуются различные оценки, например:

  • Золотой стандарт (с использованием стандартной онтологии)
  • Экспертная оценка (формирование онтологии людьми)

См. также

Примечания

  1. ↑ Wikipedia — Semantic Network
  2. ↑ Knowledge graph definition
  3. ↑ Википедия — Концептуальная схема
  4. ↑ Wikipedia — Онтологическая инженерия
  5. ↑ Wikipedia — Контролируемый словарь
  6. ↑ Wikipedia — OWL
  7. ↑ Wikipedia — KIF
  8. ↑ Wikipedia — Common Logic
  9. ↑ Wikipedia — CycL
  10. ↑ Wikipedia — DAML+OIL
  11. ↑ Wikipedia — Resource Description Framework
  12. ↑ Wikipedia — Part-of-speech tagging
  13. ↑ Wikipedia — Lemmatisation
  14. ↑ Wikipedia — Subcategorization Frames
  15. ↑ Wikipedia — Contrastive analysis
  16. ↑ Wikipedia — Formal concept analysis
  17. ↑ Wikipedia — Inductive Logic Programming

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Представление_знаний&oldid=76603»