Проблемы нейронных сетей
Проблема взрывающегося (исчезающего) градиента в нейронных сетях
Постановка проблемы
Напомним, что градиентом в нейронных сетях называется вектор частных производных функции потерь по весам нейронной сети. Таким образом, он указывает на направление наибольшего роста этой функции для всех весов по совокупности. Градиент считается в процессе тренировки нейронной сети и используется в оптимизаторе весов для улучшения качества модели.
В процессе обратного распространения ошибки при прохождении через слои нейронной сети в элементах градиента могут накапливаться большие значения, что будет приводить к сильным изменениям весов. Это свою очередь может сделать нестабильным алгоритм обучения нейронной сети. В таком случае элементы градиента могут переполнить тип данных, в котором они хранятся. Такое явление называется взрывающимся градиентом (англ. exploding gradient).
Существует аналогичная обратная проблема, когда в процессе обучения при обратном распространении ошибки через слои нейронной сети градиент становится все меньше. Это приводит к тому, что веса при обновлении изменяются на слишком малые значения, и обучение проходит неэффективно или останавливается, то есть алгоритм обучения не сходится. Это явление называется исчезающим градиентом (англ. vanishing gradient).
Таким образом, увеличение числа слоев нейронной сети с одной стороны увеличивает ее способности к обучению и расширяет ее возможности, но с другой стороны может порождать данную проблему. Поэтому для решения сложных задач с помощью нейронных сетей необходимо уметь определять и устранять ее.
Причины
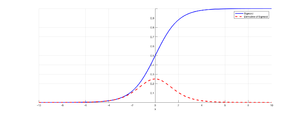
В нейронных сетях классической функцией активации (англ. activation function) для слоев является сигмоида (англ. sigmoid):
$\sigma(x) = \frac{1}{1 + e^{-x}}$
Посчитаем производную по слоям $u_d, u_{d-1}, \dots$, где $L$ — функция потерь (англ. loss function), $w$ — вес, $a$ — выход по производной. Оценка для производной видна из рис. 1.
$\frac{\partial(L(w))}{\partial(u_d)} = \frac{\partial(L(w))}{\partial(a)} \cdot \frac{\partial(a)}{\partial(u_d)} = (y - a) \cdot \sigma'(w_d u_d) w_d \leq 2 \cdot \frac{1}{4} w_d$
$\frac{\partial(L(w))}{\partial(u_{d - 1})} = \frac{\partial(L(w))}{\partial(u_d)} \cdot \frac{\partial(u_d)}{\partial(u_{d - 1})} \leq 2 \cdot (\frac{1}{4})^2 w_d w_{d-1}$
$\ldots$
Откуда видно, что оценка градиента растет экспоненциально при увеличении числа слоев. Это в свою очередь может приводить либо к экспоненциальному росту градиента от слоя к слою, либо к затуханию.
Способы определения
Взрывающийся градиент
Возникновение проблемы взрывающегося градиента можно определить по следующим признакам:
- Модель плохо обучается на данных, что отражается в высоком значении функции потерь;
- Модель нестабильна, что отражается в значительных скачках значения функции потерь;
- Значение функции потерь принимает значение
NaN.
Более непрозрачные признаки, которые могут подтвердить возникновение проблемы:
- Веса модели растут экспоненциально;
- Веса модели принимают значение
NaN.
Затухающий градиент
Признаки проблемы затухающего градиента:
- Модель медленно улучшает свою точность, при этом возможно раннее срабатывание критерия останова, так как алгоритм может решить, что дальнейшее обучение не окажет существенного влияния на качество модели;
- Градиент ближе к концу показывает более сильные изменения, в то время как градиент ближе к началу почти не показывает никакие изменения;
- Веса модели уменьшаются экспоненциально во время обучения;
- Веса модели стремятся к $0$ во время обучения.
Способы устранения
Использование другой функции активации
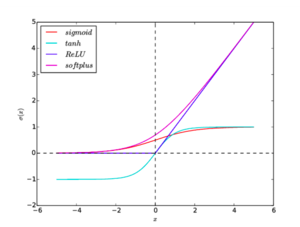
Tanh
$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
Функция аналогична сигмоиде, но множество возможных значений: $[-1, 1]$. Градиенты при этом сосредоточены около $0$.
ReLU
$h(x) = \max(0, x)$
Функция проста для вычисления и имеет производную, равную либо $1$, либо $0$. Также есть мнение, что именно эта функция используется в биологических нейронных сетях. Недостатком функции является отсутствие производной в нуле, что можно устранить доопределением производной в нуле слева или справа. Также эту проблему устраняет использование гладкой аппроксимации, Softplus.
Существуют модификации ReLU:
- Noisy ReLU: $h(x) = \max(0, x + \varepsilon), \varepsilon \sim N(0, \sigma(x))$;
- Parametric ReLU: $h(x) = \begin{cases} x & x > 0 \\ \beta x & \text{otherwise} \end{cases}$;
- Leaky ReLU: Paramtetric ReLU со значением $\beta = 0.01$.
Softplus
$h(x) = \ln(1 + e^x)$
Гладкий, везде дифференцируемый аналог ReLU. Однако, эта функция более сложна для вычисления. Эмпирически было выявлено, что по качеству не превосходит ReLU.
Графики всех функций активации приведены на рис. 2.
Изменение модели
В глубоких нейронных сетях для решения проблемы может оказаться достаточным сокращение числа слоев. Также может помочь уменьшение размера батчей.
В рекуррентных нейронных сетях можно воспользоваться техникой обрезания обратного распространения ошибки по времени, которая заключается в обновлении весов с определенной периодичностью.
Использование Residual blocks
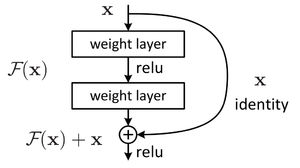
В данной конструкции вывод нейрона подается как следующему нейрону, так и нейрону на расстоянии 2-3 впереди, который суммирует его с выходом предшествующего нейрона, а функция активации в нем — ReLU (см. рис. 3). Это позволяет при обратном распространении ошибки влиять градиенту на более далекие слои напрямую.
Регуляризация весов
Регуляризация заключается в том, что слишком большие значения весов будут увеличивать функцию потерь, таким образом штрафуя за этой нейронную сеть.
Обрезание градиента
Образание заключается в ограничении нормы градиента. То есть если норма градиента превышает заранее выбранную величину, то следует сократить ее до данной величины, не изменив направление.