Граф компонент рёберной двусвязности
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Определение: |
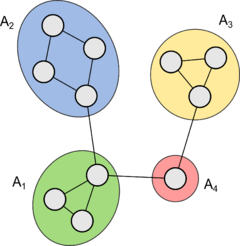
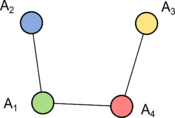
| Пусть граф связен. Обозначим — компоненты рёберной двусвязности, а — мосты . Построим граф , в котором вершинами будут , а рёбрами — , соединяющими соответствующие вершины из соответствующих компонент рёберной двусвязности. Полученный граф называют графом компонент рёберной двусвязности (англ. costal doubly-linked components graph) графа . |
| Лемма: |
В определении, приведенном выше, — дерево. |
| Доказательство: |
|