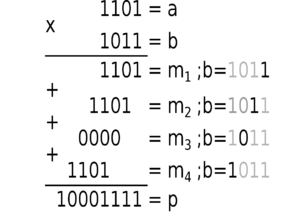Матричный умножитель

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Принцип работы

Умножение в бинарной системе

Умножение в столбик

Умножение в бинарной системе счисления происходит точно так же, как в десятичной — по схеме умножения столбиком. Если множимое — [math]k[/math] разрядное, а множитель — [math]n[/math] разрядный, то для формирования произведения требуется вычислить [math]n[/math] частичных произведений и сложить их между собой.

Вычисление частичных произведений

В бинарной системе для вычисления частичного произведения можно воспользоваться логическими элементами [math]\&[/math] — конъюнкторами. Каждое частичное произведение [math](m_i)[/math] — это результат выполнения [math]k[/math] логических операции [math]\&[/math] ( между текущим [math]i[/math], где [math]i=1..n[/math], разрядом множителя и всеми [math]k[/math] разрядами множимого) и сдвига результата логической операции влево на число разрядов, соответствующее весу текущего разряда множителя. Матричный умножитель вычисляет частичные произведения по формуле:

[math]m_i = 2^{i - 1} (a \& b_i), (i=1..n)[/math]

Суммирование частичных произведений

На этом этапе происходит сложение всех частичных произведений [math] m [/math].

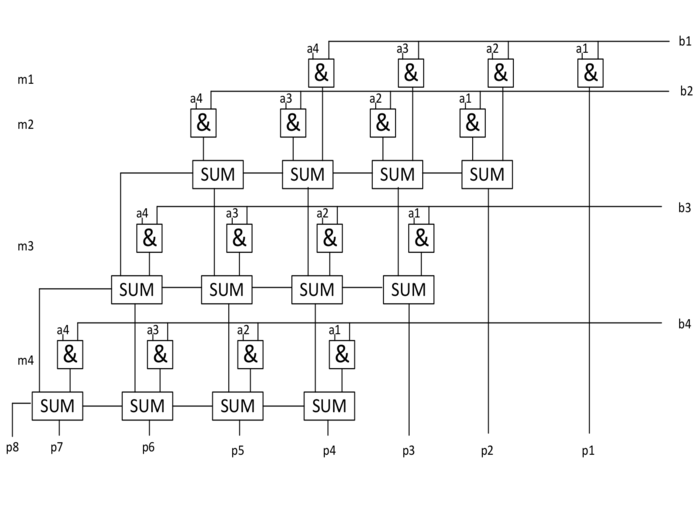
Схема

Схема матричного умножителя

Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик для двух четырёх — разрядных чисел приведена на рисунке. Формирование частичных произведений осуществляется посредством логических элементов [math]\&[/math]. Полные одноразрядные сумматоры обеспечивают формирование разрядов результата. Разрядность результата — [math]l[/math] определяется разрядностью множителя — [math]n[/math] и множимого — [math]k[/math]:

[math] l=n+k [/math].

Все конъюнкторы работают параллельно. Полные одноразрядные сумматоры обеспечивают поразрядное сложение результатов конъюнкций и переносов из предыдущих разрядов сумматора. В приведенной схеме использованы четырех разрядные сумматоры с последовательным переносом. Время выполнения операции умножения определяется временем распространения переносов до выходного разряда [math] p8 [/math].

Матричный умножитель

Если внимательно посмотреть на схему матричного умножителя (англ. binary multiplier), то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа [math]A[/math] и числа [math]B[/math]. В точках пересечения этих проводников находятся логические элементы [math]\&[/math]. Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.

Схемная сложность

Частичные произведения вычисляются за [math]n[/math] шагов. Сложение с вычислением переносов включает [math]n - 1[/math] шаг. Последнее сложение можно выполнить за [math]O(\log n)[/math].

В итоге суммарное время работы:

[math]O(n) + O(n) + O(\log n) = O(n) [/math]

Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом, приведенным на первом рисунке (общая схема), а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т.д. В этом случае время выполнения операции умножения значительно сократится.

Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей, однако ничего не бывает бесплатно. В обмен на быстродействие придётся заплатить увеличением разрядности сумматоров, а значит сложностью схемы.

Есть и более быстрые способы умножения двух чисел, например умножение с помощью дерева Уоллеса, которое работает [math]O(\log n)[/math].

См. также

• Дерево Уоллеса
• Двоичный каскадный сумматор

Источники информации

• Е. Угрюмов "Цифровая схемотехника" 2001г.

• Дк. Ф. Уэйкерли "Проектирование цифровых устройств, том 1." 2002г.

• М.И. Богданович "Цифровые интегральные микросхемы" 1996г.

• Схема умножителя

• Кормен Т., Лейзерсон Ч., Ривест Р.. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5