Ppi1riintegerLmax
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Задача: |
| Дано однородных станков, работающих параллельно, и работ с временем выполнения , временем появления , заданным целым числом, и моментом времени , к которому нужно выполнить работу. Необходимо построить такое расписание, чтобы значение максимального опоздания было минимальным. |
Содержание
Описание алгоритма
Идея
Отсортируем все работы по времени появления в неубывающем порядке так, что . Теперь будем выполнять доступные на данный момент работы в порядке неубывания дедлайнов . То есть, если в момент времени есть свободные станки и есть невыполненные работы такие, что , то назначаем работу с наименьшим дедлайном на свободный станок.
Псевдокод
Алгоритм принимает на вход массив пар, где первый элемент является временем появления работы, а второй её дедлайном , и возвращает расписание, представленное массивом, где на позиции стоит момент обработки работы .
function scheduling(jobs: <int, int>[n]) -> int[n]
sort(jobs) // сортируем работы в порядке неубывания времени появления
int j = 1 // последняя невыполненная работа
int[n] ans // массив, куда будет записано расписание
Heap<int> M // куча, в которой будем хранить доступные на данный момент работы в порядке неубывания дедлайнов
while j <= n
int time = jobs[j].first // время начала выполнения текущего блока работ
while jobs[j].first <= time // добавляем в кучу все невыполненные работы, доступные на данный момент
M.push(j)
j++
int k = 0 // количество занятых станков в данный момент времени
while M.notEmpty
i = M.pop() // получаем доступную работу с наименьшим дедлайном
ans[i] = t // назначаем работу i на время t
if k + 1 < m // если в момент t есть свободный станок, то назначаем работу i на него
k++
else // иначе увеличиваем время и обновляем список доступных работ
t++
k = 0
while jobs[j].first <= time
M.push(j)
j++
Внутренний цикл распределяет работы блоками, в которых они выполняются без простоя станков. После окончания такого блока, время начала выполнения следующего будет равно текущему значению .
Асимптотика
Сначала мы сортируем работы, что занимает . Далее идёт цикл, в котором мы раз кладём элемент в кучу и раз извлекаем, что также занимает времени. В итоге всё вместе составляет асимптотику алгоритма .
Замечание
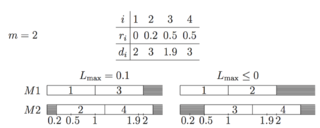
Стоит отметить тот факт, что если снять ограничение на целочисленность и позволить им принимать вещественные значения, то представленный алгоритм перестанет строить оптимальное расписание, как видно из контрпримера.
Доказательство корректности алгоритма
| Теорема: |
Приведенный алгоритм строит оптимальное расписание для задачи . |
| Доказательство: |
|
Пусть — расписание построенное предложенным алгоритмом, а оптимальное расписание со следующими свойствами:
|
См. также
Источники информации
- Peter Brucker «Scheduling Algorithms», fifth edition, Springer — с. 111-112 ISBN 978-3-540-69515-8