Теорема о существовании простого цикла в случае существования цикла

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Лемма:

Наличие двух различных рёберно простых путей между какими-либо двумя вершинами неориентированного графа [math]G[/math] равносильно наличию цикла в этом графе.

Доказательство:

[math]\triangleright[/math]

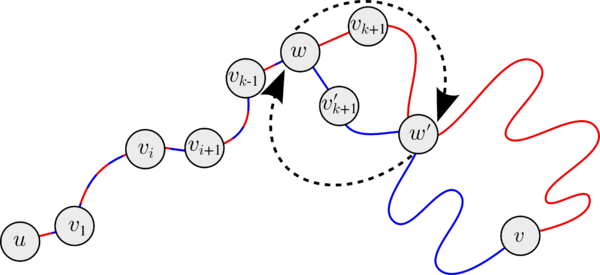
[math]\Rightarrow[/math] Предположим, что в графе [math]G[/math] существует два различных рёберно простых пути между вершинами [math]u[/math] и [math]v[/math]. Пусть это будут пути [math]p = u e_1 v_1\ldots v_{n-1} e_n v[/math] и [math]p' = u e'_1 v'_1\ldots v'_{n-1} e'_n v[/math]. Пусть их наибольший общий префикс заканчивается в вершине [math]w = v_k = v'_k[/math]. Заметим, что [math]w \neq v[/math], т.к. пути различны. Рассмотрим суффиксы путей [math]p[/math] и [math]p'[/math]: [math]s = w e_{k+1} \ldots v[/math] и [math]s' = w e'_{k+1} \ldots v[/math] соответственно. Найдём первую совпадающую вершину [math]w'[/math] в [math]s[/math] и [math]s'[/math], не равную [math]w[/math]. Осталось заметить, что замкнутый путь [math]c[/math], полученный объединением [math]w \leadsto w'[/math] части пути [math]s[/math] вместе с [math]w' \leadsto w[/math] частью цепи [math]s'[/math], является циклическим путем. Действительно, в путях [math]s[/math] и [math]s'[/math] двух одинаковых рёбер подряд не бывает, т.к. это рёберно простые пути, а рёбра, смежные с [math]w[/math] и [math]w'[/math], не совпадают по построению. Циклический путь [math]c[/math] является представителем некоторого цикла в графе [math]G[/math]. [math]\Leftarrow[/math] Предположим, что в графе [math]G[/math] существует цикл и пусть циклический путь [math]c = v_0 e_1 v_1 \ldots e_n v_0[/math] — его представитель. Найдём первую точку [math]w = v_k = v_l (l \gt k)[/math] пересечения [math]c[/math] с самим собой. Такая точка существует, т.к. путь замкнутый. Рассмотрим циклический путь [math]v_k e_{k+1} \ldots e_l v_l[/math]: он простой, т. к. если это неверно и существует вершина [math]v_j = v_j' (k \lt j \lt j' \lt l)[/math], то в [math]c[/math] вершина [math]v_j'[/math] повторяется раньше, чем [math]v_l[/math]. Теперь элементарно взяв две вершины [math]v_k[/math] и [math]v_{k+1}[/math] легко заметить, что существует два различных рёберно непересекающихся пути между ними: [math]v_k e_{k+1} v_{k+1}[/math] и [math]v_k e_l v_{l - 1} \ldots v_k[/math].

[math]\triangleleft[/math]

Иллюстрация к лемме: пути отмечены соответственно красным и синим (их общий префикс отмечен пунктиром), а циклический путь [math]c[/math] проходит вдоль чёрных стрелок

Теорема:

Если в неориентированном графе существует цикл, то в этом графе существует простой цикл.

Доказательство:

[math]\triangleright[/math]

Выберем в графе минимальный по количеству рёбер цикл (он существует, потому что количество рёбер в любом цикле — натуральное число ). Предположим, что он не простой. Но тогда он содержит дважды одну и ту же вершину, т. е. содержит в себе цикл меньшего размера, что противоречит тому, что наш цикл минимальный. Таким образом, этот цикл — простой.

[math]\triangleleft[/math]

В графе минимальный цикл включает в себя три ребра — например, [2 - 5 - 6] (выделен красным). Согласно теореме, он является простым.

Замечания

• Так как вершинно-простой путь всегда является рёберно-простым, первая теорема справедлива и для вершинно-простых путей (усиление условия).
• Так как вершинно-простой цикл всегда является рёберно-простым, первая теорема справедлива и для рёберно-простого цикла (ослабление результата).

Утверждение (неверное):

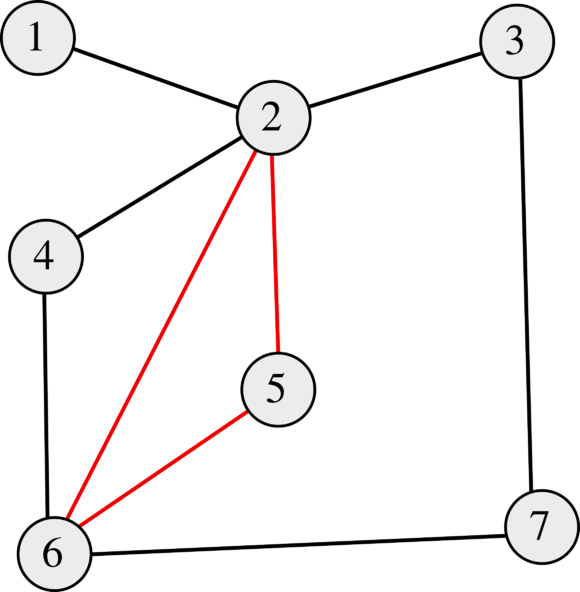
Если две вершины графа лежат на цикле, то они лежат на простом цикле.

[math]\triangleright[/math]

В общем случае неверно, так как эти вершины могут лежать в разных компонентах вершинной или рёберной двусвязности: все пути из одной вершины в другую будут содержать одну и ту же точку сочленения или один и тот же мост.

[math]\triangleleft[/math]

См. также

• Теорема о существовании простого пути в случае существования пути
• Отношение рёберной двусвязности
• Отношение вершинной двусвязности