Разрез, лемма о потоке через разрез
Версия от 19:27, 4 сентября 2022; Maintenance script (обсуждение | вклад) (rollbackEdits.php mass rollback)
| Определение: |
| -разрезом (англ. s-t cut) в сети называется пара множеств , удоволетворяющих условиям:
|
| Определение: |
| Пропускная способность разреза (англ. capacity of the cut) обозначается и вычисляется по формуле: . |
| Определение: |
| Поток в разрезе (англ. flow in the cut) обозначается и вычисляется по формуле: . |
| Определение: |
| Минимальным разрезом (англ. minimum cut) называется разрез с минимально возможной пропускной способностью |
| Лемма (о величине потока): |
Пусть — разрез в . Тогда . |
| Доказательство: |
|
|
| Лемма (закон слабой двойственности потока и разреза): |
Пусть — разрез в . Тогда . |
| Доказательство: |
| , из-за ограничений пропускных способностей . |
| Лемма (о максимальном потоке и минимальном разрезе): |
Если , то поток — максимален, а разрез — минимален. |
| Доказательство: |
|
Из закона слабой двойственности следует, что для любых двух разрезов и в сети , так как . Значит, если расположить все величины потоков и разрезов на оси OX, то у потоков с разрезами может быть максимум 1 точка пересечения. Очевидно, что эта точка определяет максимальный поток среди всех потоков и минимальный разрез среди всех разрезов сети . |
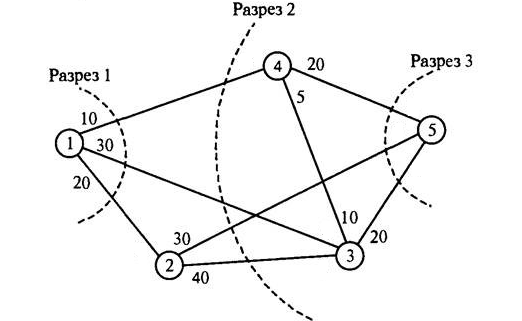
| Разрез | "Разрезанные" ребра | Пропускная способность |
| 1 | (1,2),(1,3),(1,4) | 10+30+20=60 |
| 2 | (1,3),(1,4),(2,3),(2,5) | 30+10+40+30=110 |
| 3 | (2,5),(3,5),(4,5) | 30+20+20=70 |
Источники информации
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
- Википедия: Разрез графа
- Википедия: Разрез графа (англ.)