Эта статья находится в разработке!
Определение
Сеть Бетчера (Batcher odd-even mergesort) - сортирующая сеть размером [math]O(n \log^2n)[/math] и глубиной [math]O(\log^2n)[/math], где [math]n[/math] - количество элементов для сортировки.
Конструирование сети
Для начала введем понятие битонической последовательности:
| Определение: |
| Битонической последовательностью называется последовательность, которая сначала монотонно возрастает, а затем монотонно убывает, или последовательность, которая приводится к такому виду путем циклического сдвига. |
В нашем случае мы будем рассматривать нуль-единичные битонические последовательности:
| Определение: |
| Нуль-единичные битонические последовательности - последовательности вида [math]0^i1^j0^k[/math] или [math]1^i0^j1^k[/math] для [math]i,j,k\le0[/math] |
Битонический сортировщик
На первом этапе конструирования стоит задача построить сравнивающую сеть, которая будет сортировать любую нуль-единичную битоническую последовательность - битонический сортировщик.
Полуфильтр
Битонический сортировщик состоит из нескольких каскадов, каждый из которых называется полуфильтром (half-cleaner). Каждый полуфильтр - сравнивающая сеть глубиной 1, в которой [math]i[/math]-й входной провод сравнивается со входным проводом с номером [math]i+\frac{n}{2}[/math], где [math]i=1,2,...,\frac{n}{2}[/math].
| Лемма: |
Если на вход в полуфильтр подать битоническую последовательность из нулей и единиц длиной [math]n[/math], то на выходе мы получим две битонические последовательности длиной [math]\frac{n}{2}[/math] такие, что каждый элемент из верхней последовательности не превосходит любой элемент из нижней, и что одна из них будет однородной (clean) - состоящей либо из нулей, либо из единиц.
|
| Доказательство: |
| [math]\triangleright[/math] | |
Для всех [math]i=1,2,...,\frac{n}{2}[/math] полуфильтр сравнивает провода с номерами [math]i[/math] и [math]i+\frac{n}{2}[/math]. Без потери общности будем рассматривать входную последовательность вида [math]0...01...10...0[/math] (для последовательности вида [math]1...10...01...1[/math] рассуждения аналогичны). В зависимости от того в каком блоке из последовательно расположенных нулей и единиц находится средняя точка [math]\frac{n}{2}[/math] входной последовательности, можно выделить 3 случая, причем один из случаев (когда средняя точка попадает на блок из единиц) можно разбить еще на 2 случая. Все 4 случая разобраны на рис. 2. Для каждого из ни лемма выполняется. | | [math]\triangleleft[/math] |
|
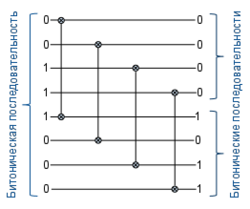 Рис.1 Полуфильтр для 8 проводов |

Рис.2 Все случаи попадания битонической последовательности на полуфильтр
Битонический сотрировщик

