Турниры — различия между версиями
Roman (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition = '''Турнир''' — [[ориентированный граф]], между любой парой различных вершин которого есть ровно одно ориентированное ребро. | + | |definition = '''Турнир''' (англ. ''Tournament'') — [[ориентированный граф]], между любой парой различных вершин которого есть ровно одно ориентированное ребро. |
}} | }} | ||
| Строка 6: | Строка 6: | ||
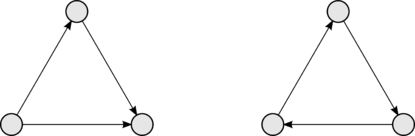
[[Файл:Tournament_1_3.png|415px|thumb|left|Турниры из трех вершин]] | [[Файл:Tournament_1_3.png|415px|thumb|left|Турниры из трех вершин]] | ||
| − | |||
| − | |||
<br clear="all"> | <br clear="all"> | ||
| + | ==Оценка количества турниров в графе== | ||
| + | Если в турнире опустить ориентацию ребер, то мы получим полный граф. А так как существует два варианта ориентации каждого ребра, то количество турниров в графе из <tex>n</tex> вершин равно <tex dpi=150>2^{\frac{n\cdot(n-1)}{2}}</tex>. | ||
==Сильно связные турниры== | ==Сильно связные турниры== | ||
{{Определение|definition = Турнир называется [[Отношение связности, компоненты связности#sc_def |сильно связным]], если из любой вершины существуют пути до всех других.}} | {{Определение|definition = Турнир называется [[Отношение связности, компоненты связности#sc_def |сильно связным]], если из любой вершины существуют пути до всех других.}} | ||
| Строка 32: | Строка 32: | ||
* [[Теорема Редеи-Камиона]] | * [[Теорема Редеи-Камиона]] | ||
| − | == | + | ==Источники информации== |
* Асанов М. О., Баранский В. А., Расин В. В. '''Дискретная математика: графы, матроиды, алгоритмы''' — НИЦ РХД, 2001. — ISBN 5-93972-076-5 | * Асанов М. О., Баранский В. А., Расин В. В. '''Дискретная математика: графы, матроиды, алгоритмы''' — НИЦ РХД, 2001. — ISBN 5-93972-076-5 | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Обходы графов]] | [[Категория: Обходы графов]] | ||
Версия 14:29, 7 ноября 2015
| Определение: |
| Турнир (англ. Tournament) — ориентированный граф, между любой парой различных вершин которого есть ровно одно ориентированное ребро. |
Название этого класса графов связано с тем, что их удобно использовать для описания результатов командных соревнований в некоторых видах спорта.
Содержание
Оценка количества турниров в графе
Если в турнире опустить ориентацию ребер, то мы получим полный граф. А так как существует два варианта ориентации каждого ребра, то количество турниров в графе из вершин равно .
Сильно связные турниры
| Определение: |
| Турнир называется сильно связным, если из любой вершины существуют пути до всех других. |
| Определение: |
| Турнир называется гамильтоновым, если он содержит гамильтонов цикл. |
Не все турниры гамильтоновы. Определение не исключает существование вершины с полустепенью исхода или захода равной нулю — в первую нельзя войти, а из второй — выйти. Однако отсутствие таких вершин не означает, что турнир гамильтонов (пример — на рисунке справа).
Теорема Редеи-Камиона устанавливает 2 следующих факта:
- Все турниры полугамильтоновы.
- Турнир гамильтонов тогда и только тогда, когда он сильно связен.
См. также
Источники информации
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — ISBN 5-93972-076-5