|
|
| Строка 42: |
Строка 42: |
| | 2 | | 2 |
| | |statement= | | |statement= |
| − | Количество дополняющих путей с масштабом <tex> 2^k </tex> не превосходит <tex> 2E </tex>.
| + | Суммарное количество увеличивающих путей {{---}} <tex> O(E \log U) </tex>. |
| − | |proof=
| |
| − | | |
| − | На предыдущей итерации по предыдущей лемме. Следовательно, количество дополняющих путей не превосходит <tex> 2E </tex>.
| |
| − | }} | |
| − | | |
| − | {{Лемма
| |
| − | |about=
| |
| − | 2
| |
| − | |statement=
| |
| − | Общее количество увеличивающих путей не превышает <tex> O(E \log U) </tex>.
| |
| | |proof= | | |proof= |
| | На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше <tex> 2^k </tex>. | | На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше <tex> 2^k </tex>. |
| | Дополняющий поток на предыдущей итерации ограничен значением <tex> 2^{k + 1} E </tex>. Следовательно, на каждой итерации количество дополняющих путей не превосходит <tex> 2E </tex>. | | Дополняющий поток на предыдущей итерации ограничен значением <tex> 2^{k + 1} E </tex>. Следовательно, на каждой итерации количество дополняющих путей не превосходит <tex> 2E </tex>. |
| | | | |
| − | Следует из предыдущей леммы и факта, что количество итераций {{---}} <tex> O(\log U) </tex>.
| + | Количество итераций алгоритма {{---}} <tex> O(\log U) </tex>, значит, суммарное количество увеличивающих путей {{---}} <tex> O(E \log U) </tex>. |
| | }} | | }} |
| | | | |
Версия 00:24, 7 марта 2012
Алгоритм
Алгоритм масштабирования потока — алгоритм поиска максимального потока, основывающийся на предположении, что пропускные способности всех ребер выражаются целыми числами.
Пусть дана сеть [math] G [/math], все ребра которой имеют целочисленную пропускную способность. Обозначим за [math] U [/math] максимальную пропускную способность: [math] U = \max\limits_{(u, v) \in E} c(u, v) [/math].
Идея алгоритма заключается в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать поток по ним, а затем по всем остальным. Для этого воспользуемся масштабом [math] \Delta [/math]. Изначально положим [math] \Delta = 2^{\lfloor \log_2 U \rfloor} [/math].
На каждой итерации в дополняющей сети алгоритм находит дополняющие пути с пропускной способностью не меньшей [math] \Delta [/math] и увеличивает поток вдоль них.
Уменьшив масштаб [math] \Delta [/math] в [math] 2 [/math] раза, переходит к следующей итерации.
Очевидно, что при [math] \Delta = 1 [/math] алгоритм вырождается в алгоритм Эдмондса-Карпа, вследствие чего является корректным.
Количество необходимых увеличений путей, основанных на кратчайших путях, может быть много больше количества увеличений, основанных на путях с высокой пропускной способностью.
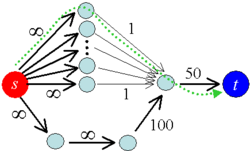 Выбор дополняющих путей в порядке длины |
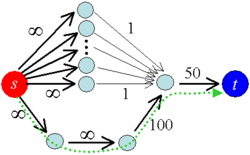 Выбор пути с высокой пропускной способностью в первую очередь |
Оценка времени работы
| Утверждение: |
Время работы алгоритма — [math] O(E^2 \log U) [/math]. |
| [math]\triangleright[/math] |
|
В ходе выполнения алгоритма масштаб [math] \Delta [/math] принимает следующие значения: [math] S = \{2^{\lfloor \log_2 U \rfloor}, \ldots, 2^k, \ldots, 2, 1, 0\} [/math]. Тогда [math] |S| = O(\log U) [/math] — количество итераций алгоритма.
| Лемма (1): |
Максимальный поток в сети [math] G [/math] ограничен сверху значением [math] |f_k| + 2^k E [/math], где [math] |f_k| [/math] — значение потока при масштабе [math] \Delta = 2^k [/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
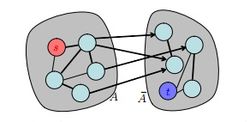 Разрез [math] C_k [/math]В конце итерации с масштабом [math] \Delta = 2^k [/math], сеть [math] G_{f_k} [/math] может быть разбита на два непересекающихся множества [math] A_k [/math] и [math] \overline{A_k} [/math] так, что остаточная пропускная способность каждого ребра, идущего из [math] A_k [/math] в [math] \overline{A_k} [/math], не превосходит масштаба [math] \Delta [/math]. То есть образуется разрез [math] C_k = \langle A_k, \overline{A_k} \rangle [/math].
При этом, количество таких ребер не превосходит [math] E [/math].
Значит, значение остаточного потока не может превосходить [math] \Delta E = 2^k E [/math]. | | [math]\triangleleft[/math] |
| Лемма (2): |
Суммарное количество увеличивающих путей — [math] O(E \log U) [/math]. |
| Доказательство: |
| [math]\triangleright[/math] | |
На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше [math] 2^k [/math].
Дополняющий поток на предыдущей итерации ограничен значением [math] 2^{k + 1} E [/math]. Следовательно, на каждой итерации количество дополняющих путей не превосходит [math] 2E [/math].
Количество итераций алгоритма — [math] O(\log U) [/math], значит, суммарное количество увеличивающих путей — [math] O(E \log U) [/math]. | | [math]\triangleleft[/math] |
Алгоритм обхода в ширину находит каждый дополняющий путь за время [math] O(E) [/math]. Следовательно, суммарное время работы алгоритма — [math] O(E^2 \log U) [/math]. |
| [math]\triangleleft[/math] |
Псевдокод
Max_Flow_By_Scaling(G,s,t)
[math] f \leftarrow 0 [/math]
[math] \Delta \leftarrow 2^{\lfloor\log_2U\rfloor} [/math]
while [math] \Delta \geq 1 [/math]
do while в [math] G_f [/math] существует увеличивающий путь [math] p [/math] с пропускной способностью не меньшей [math] \Delta [/math]
do [math] \delta \leftarrow \min\{c(u, v) \colon(u, v) \in p\} [/math]
увеличить поток по рёбрам [math] p [/math] на [math] \delta [/math]
обновить [math] G_f [/math]
[math] f \leftarrow f + \delta [/math]
[math] \Delta \leftarrow \Delta / 2 [/math]
return [math] f [/math]
Литература


