Двойственный граф планарного графа — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
м (Переделал с помощью исправленного шаблона определения)
Строка 13: Строка 13:
  
 
«…Для данного плоского графа ''G'' его ''двойственный граф G&prime; ''строится следующим образом: поместим в каждую область ''G'' (включая внешнюю) по одной вершине графа ''G&prime;'' и, если две области имеют общее ребро ''x'', соединим помещенные в них вершины ребром ''x&prime;'', пересекающим только ''x''. В результате всегда получится плоский псевдограф. Ясно, что ''G&prime;'' имеет петлю тогда и только тогда, когда в ''G'' есть концевая вершина; ''G&prime;'' имеет кратные рёбра тогда и только тогда, когда две области графа ''G'' содержат по крайней мере два общих ребра. Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф или мультиграф, в то время как двойственный граф трёхсвязного плоского графа всегда представляет собой граф. Другими примерами двойственных графов являются платоновы графы: тетраэдр — самодвойственный граф, куб и октаэдр — двойственные, так же как додекаэдр и икосаэдр…»<ref>''Харари, Ф.'' Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009. — С. 138. — ISBN 978­-5­-397­-00622­-4.</ref>.
 
«…Для данного плоского графа ''G'' его ''двойственный граф G&prime; ''строится следующим образом: поместим в каждую область ''G'' (включая внешнюю) по одной вершине графа ''G&prime;'' и, если две области имеют общее ребро ''x'', соединим помещенные в них вершины ребром ''x&prime;'', пересекающим только ''x''. В результате всегда получится плоский псевдограф. Ясно, что ''G&prime;'' имеет петлю тогда и только тогда, когда в ''G'' есть концевая вершина; ''G&prime;'' имеет кратные рёбра тогда и только тогда, когда две области графа ''G'' содержат по крайней мере два общих ребра. Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф или мультиграф, в то время как двойственный граф трёхсвязного плоского графа всегда представляет собой граф. Другими примерами двойственных графов являются платоновы графы: тетраэдр — самодвойственный граф, куб и октаэдр — двойственные, так же как додекаэдр и икосаэдр…»<ref>''Харари, Ф.'' Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009. — С. 138. — ISBN 978­-5­-397­-00622­-4.</ref>.
 +
  
 
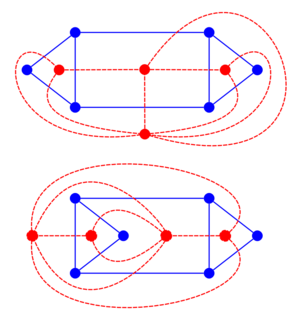
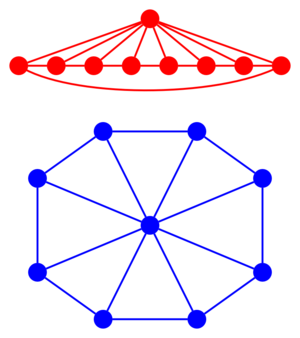
[[Файл:Noniso_dual_graphs.png|thumb|left|В верхнем двойственном графе есть вершина степени 6, а в нижнем — нет. Следовательно, они не изоморфны.]]
 
[[Файл:Noniso_dual_graphs.png|thumb|left|В верхнем двойственном графе есть вершина степени 6, а в нижнем — нет. Следовательно, они не изоморфны.]]
Строка 22: Строка 23:
 
* Мост переходит в петлю, а петля — в мост
 
* Мост переходит в петлю, а петля — в мост
 
* Мультиграф, ''двойственный'' к дереву, — цветок
 
* Мультиграф, ''двойственный'' к дереву, — цветок
 +
 +
 +
== Самодвойственные графы ==
 +
{{Определение
 +
|neat=neat
 +
|definition=Планарный граф называется '''самодвойственным''', если он изоморфен своему двойственному графу.
 +
}}
 +
<div style='clear:left;'></div>
 +
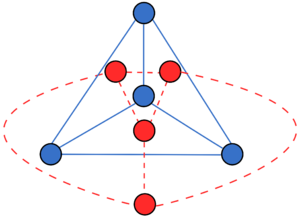
[[Файл:K4.png|thumb|left|<tex>K_4</tex> (он же кольцо).]]
 +
[[Файл:Wheel_8.png|thumb|left|Колесо и колесо.]]
 +
 +
 +
* {{Утверждение
 +
|statement=<tex>K_1</tex> и <tex>K_4</tex> — самодвойственные графы. Среди полных графов других самодвойственных нет.
 +
|proof=Проверить, что <tex>K_1</tex> и <tex>K_4</tex> полны и самодвойственны несложно. Докажем, что других нет.
 +
Поскольку грани графа переходят в рёбра, количество рёбер и граней в исходном графе должно совпадать, т.е. <tex>V = F</tex>.
 +
 +
Подставив в [[Формула Эйлера|формулу Эйлера]] имеем: <tex>2V = E + 2 \Leftrightarrow V = \frac{E}{2} + 1</tex>. В полном графе <tex>E = \frac{V \dot (V - 1)}{2}</tex>.
 +
 +
Получаем квадратное уравнение: <tex>V^2 - 5V + 4 = 0</tex>. Его решения: <tex>V_1 = 1</tex> и <tex>V_2 = 4</tex>.
 +
Таким образом, чтобы ''полный'' граф был ''самодвойственным'', в нём должна быть ровно '''одна''' или '''четыре''' вершины.
 +
}}
 +
* {{Утверждение
 +
|statement=Все колёса самодвойственны.
 +
}}
  
 
<div style="clear:both;"></div>
 
<div style="clear:both;"></div>

Версия 07:00, 18 октября 2010

Эта статья находится в разработке!


Определение:
Граф[1] G′ называется двойственным к планарному графу G, если:
  1. Вершины G′ соответствуют граням G
  2. Между двумя вершинами в G′ есть ребро тогда и только тогда, когда соответствующие грани в G имеют общее ребро
Граф (белые вершины) и двойственный ему (полосатые вершины).


«…Для данного плоского графа G его двойственный граф G′ строится следующим образом: поместим в каждую область G (включая внешнюю) по одной вершине графа G′ и, если две области имеют общее ребро x, соединим помещенные в них вершины ребром x′, пересекающим только x. В результате всегда получится плоский псевдограф. Ясно, что G′ имеет петлю тогда и только тогда, когда в G есть концевая вершина; G′ имеет кратные рёбра тогда и только тогда, когда две области графа G содержат по крайней мере два общих ребра. Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф или мультиграф, в то время как двойственный граф трёхсвязного плоского графа всегда представляет собой граф. Другими примерами двойственных графов являются платоновы графы: тетраэдр — самодвойственный граф, куб и октаэдр — двойственные, так же как додекаэдр и икосаэдр…»[2].


В верхнем двойственном графе есть вершина степени 6, а в нижнем — нет. Следовательно, они не изоморфны.

Свойства

Дерево и двойственный к нему «цветок».‎
  • Если G′ — двойственный к двусвязному графу G, то G — двойственный к G′
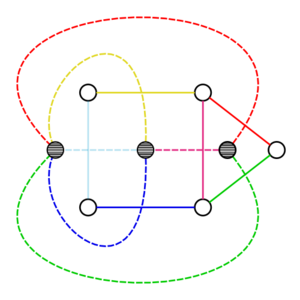
  • У одного и того же графа может быть несколько двойственных, в зависимости от конкретной укладки (см. картинку)
  • Поскольку любой трёхсвязный планарный граф допускает только одну укладку на сфере[3], у него должен быть единственный двойственный граф
  • Мост переходит в петлю, а петля — в мост
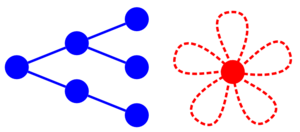
  • Мультиграф, двойственный к дереву, — цветок


Самодвойственные графы

Определение:
Планарный граф называется самодвойственным, если он изоморфен своему двойственному графу.
[math]K_4[/math] (он же кольцо).
Колесо и колесо.


  • Утверждение:
    [math]K_1[/math] и [math]K_4[/math] — самодвойственные графы. Среди полных графов других самодвойственных нет.
    [math]\triangleright[/math]

    Проверить, что [math]K_1[/math] и [math]K_4[/math] полны и самодвойственны несложно. Докажем, что других нет. Поскольку грани графа переходят в рёбра, количество рёбер и граней в исходном графе должно совпадать, т.е. [math]V = F[/math].

    Подставив в формулу Эйлера имеем: [math]2V = E + 2 \Leftrightarrow V = \frac{E}{2} + 1[/math]. В полном графе [math]E = \frac{V \dot (V - 1)}{2}[/math].

    Получаем квадратное уравнение: [math]V^2 - 5V + 4 = 0[/math]. Его решения: [math]V_1 = 1[/math] и [math]V_2 = 4[/math].

    Таким образом, чтобы полный граф был самодвойственным, в нём должна быть ровно одна или четыре вершины.
    [math]\triangleleft[/math]
    • Утверждение:
      Все колёса самодвойственны.

      Примечания

      1. ↑ На самом деле, двойственный граф — псевдограф, поскольку в нём могут быть петли и кратные рёбра.
      2. ↑ Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009. — С. 138. — ISBN 978­-5­-397­-00622­-4.
      3. ↑ Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009. — Теорема 11.5 — С. 130. — ISBN 978­-5­-397­-00622­-4.
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Двойственный_граф_планарного_графа&oldid=4142»