Двудольные графы и раскраска в 2 цвета

Определение:

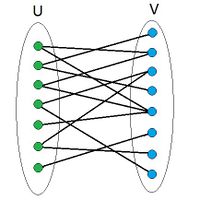
Неориентированный граф [math]G = (W,E)[/math] называется двудольным, если множество его вершин можно разбить на две части [math] U \cup V = W , \mid U\mid \gt 0, \mid V\mid \gt 0[/math], так, что ни одна вершина в [math]U[/math] не соединена с вершинами в [math]U[/math] и ни одна вершина в [math]V[/math] не соединена с вершинами в [math]V[/math].

Пример двудольного графа

Теорема (Кёниг):

Граф является двудольным [math] \iff [/math] когда все циклы четные.

Доказательство:

[math]\triangleright[/math]

Достаточность. Рассмотрим двудольный граф. Начнем цикл в доли [math] U [/math]. Нужно пройти по четному числу ребер, чтобы подняться в [math] U [/math] снова. Следовательно, при замыкании цикла число ребер будет четным. Необходимость. Если граф несвязный, то проведем доказательство отдельно для каждой компоненты. Пусть граф связный и все циклы в нем четные. Выделим произвольную вершину [math] v_0 [/math] и найдем произвольные цепи между [math] v_0 [/math] и всеми остальными вершинами (например, самые короткие алгоритмом Дейкстры). Если одна цепь [math](v_0, v_i)[/math] нечетной длины, то и любая цепь [math](v_0, v_i)[/math] нечетная, иначе бы эти цепи образовали нечетный цикл. Аналогично, если [math](v_0, v_i)[/math] — четная, то и любая [math](v_0, v_i)[/math] — четная. Разобьем вершины на две доли: в одну войдет вершина [math] v_0 [/math] и все, находящиеся от [math] v_0 [/math] на четном расстоянии; в другую долю поместим все вершины, находящиеся от [math] v_0 [/math] на нечетном расстоянии. Если вершины [math] u_1 [/math] и [math] u_2 [/math] принадлежат одной доле, то между ними не может быть ребра, иначе это ребро вместе с цепями [math](v_0, u_1)[/math] и [math](v_0, u_2)[/math] образовали бы нечетный цикл.

[math]\triangleleft[/math]

Раскраска в 2 цвета

Так как множество вершин двудольного графа можно разделить на 2 независимых подмножества так, что ни одна из вершин ни в одном из этих подмножеств не является смежной к вершине из этого же подмножества [math]\Rightarrow[/math] граф [math]G = (W,E)[/math] - 2-раскрашиваем. [math]\chi(G) = 2[/math].

Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину. На каждом шаге обхода в глубину метим вершину. Допустим мы пошли в первую вершину - добавляем ее в множество [math] U [/math]. То есть ставим метку [math] 1 [/math]. Затем просматриваем все смежные вершины и если не помечена вершина, то метим ее как [math] 2 [/math] (то есть добавляем во множество [math] V [/math] ) и рекурсивно переходим в нее. Если же она мечена и у нее такая же метка как у нашей - то все граф не двудольный.

=См. также

* Графы. Раскраски и укладки