Детерминированные автоматы с магазинной памятью, допуск по пустому стеку — различия между версиями
Zernov (обсуждение | вклад) |
|||
| Строка 21: | Строка 21: | ||
[[Файл:ДМП2.png]] | [[Файл:ДМП2.png]] | ||
}} | }} | ||
| + | |||
| + | == См. также == | ||
| + | * [[Детерминированные автоматы с магазинной памятью]] | ||
| + | * [[Автоматы с магазинной памятью]] | ||
| + | * [[МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность]] | ||
| + | * [[Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами]] | ||
| + | * [[ДМП-автоматы и неоднозначность]] | ||
==Источники информации== | ==Источники информации== | ||
Версия 15:54, 3 марта 2018
| Определение: |
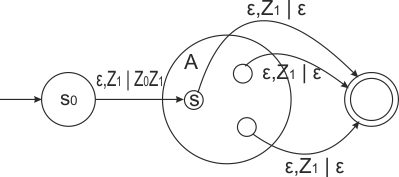
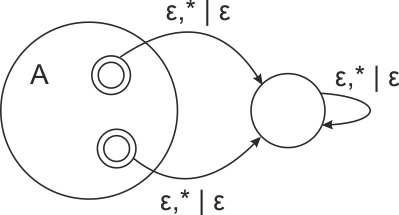
| Определим детерминированный автомат с магазинной памятью, допускающий по пустому стеку (англ. PDA accepting by empty stack), как детерминированный автомат с магазинной памятью, у которого нет множества допускающих состояний. Автомат заканчивает свою работу как только стек становится пустым. |
Определим для него множество допускающих слов , где — произвольное состояние.
| Определение: |
| Язык называется беспрефиксным (англ. prefix-free), если для любой пары слов из этого языка ни одно из этих слов не является префиксом другого. |
См. также
- Детерминированные автоматы с магазинной памятью
- Автоматы с магазинной памятью
- МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность
- Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами
- ДМП-автоматы и неоднозначность
Источники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. : ISBN 978-5-8459-1347-0 (рус.)