Кластеризация — различия между версиями
([Major] Hierarchical clustering added) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 32 промежуточные версии 10 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Файл:clusters.png|thumb|300px|Пример кластеризации]] | ||
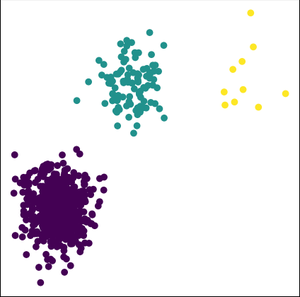
'''Кластеризация''' (англ. ''cluster analysis'') {{---}} задача группировки множества объектов на подмножества ('''кластеры''') таким образом, | '''Кластеризация''' (англ. ''cluster analysis'') {{---}} задача группировки множества объектов на подмножества ('''кластеры''') таким образом, | ||
чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров по какому-либо критерию. | чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров по какому-либо критерию. | ||
Задача кластеризации относится к классу задач обучения без учителя. | Задача кластеризации относится к классу задач обучения без учителя. | ||
| − | |||
== Постановка задачи кластеризации == | == Постановка задачи кластеризации == | ||
Пусть <tex>X</tex> {{---}} множество объектов, <tex>Y</tex> {{---}} множество идентификаторов (меток) кластеров. | Пусть <tex>X</tex> {{---}} множество объектов, <tex>Y</tex> {{---}} множество идентификаторов (меток) кластеров. | ||
| Строка 10: | Строка 10: | ||
Необходимо разбить выборку на подмножества (кластеры), то есть каждому объекту <tex>x_i \in X^m</tex> сопоставить метку <tex>y_i \in Y</tex>, | Необходимо разбить выборку на подмножества (кластеры), то есть каждому объекту <tex>x_i \in X^m</tex> сопоставить метку <tex>y_i \in Y</tex>, | ||
таким образом чтобы объекты внутри каждого кластера были близки относительно метрики <tex>\rho</tex>, а объекты из разных кластеров значительно различались. | таким образом чтобы объекты внутри каждого кластера были близки относительно метрики <tex>\rho</tex>, а объекты из разных кластеров значительно различались. | ||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| Строка 22: | Строка 21: | ||
Решение задачи кластеризации объективно неоднозначно по ряду причин: | Решение задачи кластеризации объективно неоднозначно по ряду причин: | ||
| − | * | + | * Не существует однозначного критерия качества кластеризации. Известен ряд алгоритмов, осуществляющих разумную кластеризацию "по построению", однако все они могут давать разные результаты. Следовательно, для определения качества кластеризации и оценки выделенных кластеров необходим эксперт предметной области; |
| − | * | + | * Число кластеров, как правило, заранее не известно и выбирается по субъективным критериям. Даже если алгоритм не требует изначального знания о числе классов, конкретные реализации зачастую требуют указать этот параметр<ref>[https://scikit-learn.org/stable/modules/clustering.html scikit-learn {{---}} Clustering]</ref>; |
| − | * | + | * Результат кластеризации существенно зависит от метрики. Однако существует ряд рекомендаций по выбору метрик для определенных классов задач.<ref>Cornwell, B. (2015). Linkage Criteria for Agglomerative Hierarchical Clustering. Social Sequence Analysis, 270–274</ref>. |
| − | + | ||
| + | Число кластеров фактически является гиперпараметром для алгоритмов кластеризации. Подробнее про другие гиперпараметры и их настройку можно прочитать в статье<ref>Shalamov Viacheslav, Valeria Efimova, Sergey Muravyov, and Andrey Filchenkov. "Reinforcement-based Method for Simultaneous Clustering Algorithm Selection and its Hyperparameters Optimization." Procedia Computer Science 136 (2018): 144-153.</ref>. | ||
| + | |||
| + | == Теорема невозможности Клейнберга == | ||
| + | Для формализации алгоритмов кластеризации была использована аксиоматическая теория. Клейнберг постулировал три простых свойства в качестве аксиом кластеризации и доказал теорему, связывающую эти свойства. | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | Алгоритм кластеризации <tex>a</tex> является '''масштабно инвариантным''' (англ. ''scale-invariant''), если для любой функции расстояния <tex>\rho</tex> и любой константы <tex>\alpha > 0</tex> результаты кластеризации с использованием расстояний <tex>\rho</tex> и <tex>\alpha\cdot\rho</tex> совпадают. | ||
| + | }} | ||
| + | Первая аксиома интуитивно понятна. Она требует, чтобы функция кластеризации не зависела от системы счисления функции расстояния и была нечувствительна к линейному растяжению и сжатию метрического пространства обучающей выборки. | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Полнота''' (англ. ''Richness''). Множество результатов кластеризации алгоритма <tex>a</tex> в зависимости от изменения функции расстояния <tex>\rho</tex> должно совпадать со множеством всех возможных разбиений множества объектов <tex>X</tex>. | ||
| + | }} | ||
| + | Вторая аксиома утверждает, что алгоритм кластеризации должен уметь кластеризовать обучающую выборку на любое фиксированное разбиение для какой-то функции расстояния <tex>\rho</tex>. | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | Функция расстояния <tex>{\rho}'</tex> является '''допустимым преобразованием''' функции расстояния <tex>\rho</tex>, если | ||
| + | #<tex>{\rho}'(x_i, x_j) \leqslant \rho(x_i, x_j)</tex>, если <tex>x_i</tex> и <tex>x_j</tex> лежат в одном кластере; | ||
| + | #<tex>{\rho}'(x_i, x_j) \geqslant \rho(x_i, x_j)</tex>, если <tex>x_i</tex> и <tex>x_j</tex> лежат в разных кластерах. | ||
| + | }} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | Алгоритм кластеризации является '''согласованным''' (англ. ''consistent''), если результат кластеризации не изменяется после допустимого преобразования функции расстояния. | ||
| + | }} | ||
| + | Третья аксиома требует сохранения кластеров при уменьшении внутрикластерного расстояния и увеличении межкластерного расстояния. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | | style="text-align:center; font-weight:bold;" colspan=3|Примеры преобразований с сохранением кластеров | ||
| + | |- | ||
| + | | style="padding:5px;" |[[Файл:cluster_0.png|300px]] | ||
| + | | style="padding:5px;" |[[Файл:clusters_scale_inv.png|300px]] | ||
| + | | style="padding:5px;" |[[Файл:cluster_consist.png|300px]] | ||
| + | |- | ||
| + | | style="text-align:center;width:305px;" | Исходное расположение объектов и их кластеризация | ||
| + | | style="text-align:center;width:305px;" | Пример масштабной инвариантности. Уменьшен масштаб по оси ординат в два раза. | ||
| + | | style="text-align:center;width:305px;" | Пример допустимого преобразования. Каждый объект в два раза приближен к центроиду своего класса. Внутриклассовое расстояние уменьшилось, межклассовое увеличилось. | ||
| + | |} | ||
| + | |||
| + | |||
| + | Исходя из этих аксиом Клейнберг сформулировал и доказал теорему: | ||
| + | {{Теорема | ||
| + | |author=Клейнберга | ||
| + | |about=о невозможности | ||
| + | |statement=Для множества объектов, состоящего из двух и более элементов, не существует алгоритма кластеризации, который был бы одновременно масштабно-инвариантным, согласованным и полным. | ||
| + | }} | ||
| + | Несмотря на эту теорему Клейнберг показал<ref>[https://www.cs.cornell.edu/home/kleinber/nips15.pdf Kleinberg J. An Impossibility Theorem for Clustering]</ref>, | ||
| + | что иерархическая кластеризация по методу одиночной связи с различными критериями останова удовлетворяет любым двум из трех аксиом. | ||
| + | |||
== Типология задач кластеризации == | == Типология задач кластеризации == | ||
=== Типы входных данных === | === Типы входных данных === | ||
| − | * Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками (англ. ''features''). Признаки могут быть как числовыми, так и | + | * Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками (англ. ''features''). Признаки могут быть как числовыми, так и категориальными; |
* Матрица расстояний между объектами. Каждый объект описывается расстоянием до всех объектов из обучающей выборки. | * Матрица расстояний между объектами. Каждый объект описывается расстоянием до всех объектов из обучающей выборки. | ||
| Строка 35: | Строка 82: | ||
=== Цели кластеризации === | === Цели кластеризации === | ||
| − | * Классификация объектов. Попытка понять зависимости между объектами путем выявления их кластерной структуры. Разбиение выборки на группы схожих объектов упрощает дальнейшую обработку данных и принятие решений, позволяет применить к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»). В данном случае стремятся уменьшить число кластеров для выявления наиболее общих закономерностей | + | * Классификация объектов. Попытка понять зависимости между объектами путем выявления их кластерной структуры. Разбиение выборки на группы схожих объектов упрощает дальнейшую обработку данных и принятие решений, позволяет применить к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»). В данном случае стремятся уменьшить число кластеров для выявления наиболее общих закономерностей; |
| − | * Сжатие данных. Можно сократить размер исходной выборки, взяв один или несколько наиболее типичных представителей каждого кластера. Здесь важно наиболее точно очертить границы каждого кластера, их количество не является важным критерием | + | * Сжатие данных. Можно сократить размер исходной выборки, взяв один или несколько наиболее типичных представителей каждого кластера. Здесь важно наиболее точно очертить границы каждого кластера, их количество не является важным критерием; |
* Обнаружение новизны (обнаружение шума). Выделение объектов, которые не подходят по критериям ни в один кластер. Обнаруженные объекты в дальнейшем обрабатывают отдельно. | * Обнаружение новизны (обнаружение шума). Выделение объектов, которые не подходят по критериям ни в один кластер. Обнаруженные объекты в дальнейшем обрабатывают отдельно. | ||
=== Методы кластеризации === | === Методы кластеризации === | ||
| − | * Графовые алгоритмы кластеризации. Наиболее примитивный класс алгоритмов. В настоящее время практически не применяется на практике | + | * Графовые алгоритмы кластеризации. Наиболее примитивный класс алгоритмов. В настоящее время практически не применяется на практике; |
| − | * Вероятностные алгоритмы кластеризации. Каждый объект из обучающей выборки относится к каждому из кластеров с определенной степенью вероятности. | + | * Вероятностные алгоритмы кластеризации. Каждый объект из обучающей выборки относится к каждому из кластеров с определенной степенью вероятности: |
| − | * | + | ** [[EM-алгоритм]]; |
| − | ** | + | * [[Иерархическая_кластеризация|Иерархические алгоритмы кластеризации]]. Упорядочивание данных путем создания иерархии вложенных кластеров; |
| − | + | * [[K-средних|Алгоритм <tex>\mathrm{k}</tex>-средних]]<sup>[на 28.01.19 не создан]</sup> (англ. ''<tex>\mathrm{k}</tex>-means''). Итеративный алгоритм, основанный на минимизации суммарного квадратичного отклонения точек кластеров от центров этих кластеров; | |
| + | * Распространение похожести (англ. ''affinity propagation''). Распространяет сообщения о похожести между парами объектов для выбора типичных представителей каждого кластера; | ||
| + | * Сдвиг среднего значения (англ. ''mean shift''). Выбирает центроиды кластеров в областях с наибольшей плотностью; | ||
| + | * Спектральная кластеризация (англ. ''spectral clustering''). Использует собственные значения матрицы расстояний для понижения размерности перед использованием других методов кластеризации; | ||
| + | * Основанная на плотности пространственная кластеризация для приложений с шумами (англ. ''Density-based spatial clustering of applications with noise'', ''DBSCAN''). Алгоритм группирует в один кластер точки в области с высокой плотностью. Одиноко расположенные точки помечает как шум. | ||
| + | |||
| + | |||
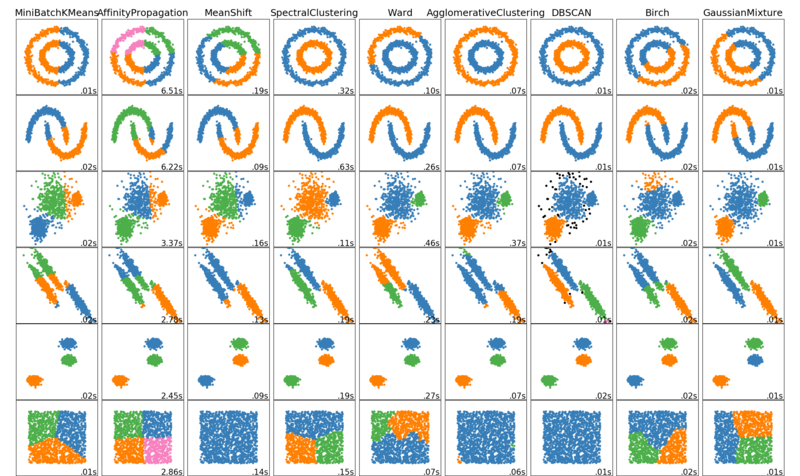
| + | [[Файл:cluster_comparison.png|thumb|800px|center|<div style="text-align:center">Сравнение алгоритмов кластеризации из пакета scikit-learn<ref>[https://scikit-learn.org/stable/auto_examples/cluster/plot_cluster_comparison.html scikit-learn {{---}} Comparing different clustering algorithms on toy datasets]</ref></div>]] | ||
| + | |||
| + | == Меры качества кластеризации == | ||
| + | Для оценки качества кластеризации задачу можно переформулировать в терминах задачи дискретной оптимизации. | ||
| + | Необходимо так сопоставить объектам из множества <tex>X</tex> метки кластеров, чтобы значение выбранного функционала качества приняло наилучшее значение. | ||
| + | В качестве примера, стремятся достичь минимума среднего внутрикластерного расстояния <tex>F_0 = \dfrac{\sum_{i<j}{[y_i=y_j]\cdot\rho(x_i, x_j)}}{\sum_{i<j}[y_i=y_j]}</tex> или максимума среднего межкластерного расстояния <tex>F_1 = \dfrac{\sum_{i<j}{[y_i\neq y_j]\cdot\rho(x_i, x_j)}}{\sum_{i<j}[y_i\neq y_j]}</tex>. | ||
| − | == | + | Подробнее про меры качества можно прочитать в статье [[Оценка_качества_в_задаче_кластеризации|оценка качества в задаче кластеризации]]. |
| − | + | ||
| − | + | == Применение == | |
| − | + | === Биология и биоинформатика === | |
| − | + | * В области экологии кластеризация используется для выделения пространственных и временных сообществ организмов в однородных условиях; | |
| − | + | * Кластерный анализ используется для группировки схожих геномных последовательностей в семейство генов, которые являются консервативными структурами для многих организмов и могут выполнять схожие функции; | |
| − | + | * Кластеризация помогает автоматически определять генотипы по различным частям хромосом; | |
| − | + | * Алгоритмы применяются для выделения небольшого числа групп генетических вариации человеческого генома. | |
| − | + | === Медицина === | |
| − | + | * Используется в позитронно-эмиссионной томографии для автоматического выделения различных типов тканей на трехмерном изображении; | |
| − | + | * Применяется для выявления шаблонов устойчивости к антибиотикам; для классификации антибиотиков по типу антибактериальной активности. | |
| + | === Маркетинг === | ||
| + | Кластеризация широко используется при изучении рынка для обработки данных, полученных из различных опросов. | ||
| + | Может применяться для выделения типичных групп покупателей, разделения рынка для создания персонализированных предложений, разработки новых линий продукции. | ||
| + | === Интернет === | ||
| + | * Выделение групп людей на основе графа связей в социальных сетях; | ||
| + | * Повышение релевантности ответов на поисковые запросы путем группировки веб-сайтов по смысловым значениям поискового запроса. | ||
| + | === Компьютерные науки === | ||
| + | * Кластеризация используется в сегментации изображений для определения границ и распознавания объектов; | ||
| + | * Кластерный анализ применяется для определения образовавшихся популяционных ниш в ходе работы эволюционных алгоритмов для улучшения параметров эволюции; | ||
| + | * Подбор рекомендаций для пользователя на основе предпочтений других пользователей в данном кластере; | ||
| + | * Определение аномалий путем построения кластеров и выявления неклассифицированных объектов. | ||
| + | |||
| + | == Псевдокод некоторых алгоритмов кластеризации == | ||
| + | === Метод K-средних (Алгоритм Ллойда) === | ||
| + | Основная идея заключается в том, что на каждой итерации перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем объекты снова разбиваются на кластеры в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике. Алгоритм завершается, когда на какой-то итерации не происходит изменения внутрикластерного расстояния. | ||
| + | |||
| + | Алгоритм минимизирует сумму квадратов внутрикластерных расстояний: | ||
| + | <tex> \sum_{i = 1}^{m} ||x_i - \mu_{a_i}||^2 \: \to \: \min_{ \{a_i\}, \{\mu_a\}}, \: \: ||x_i - \mu_a||^2 = \sum_{j = 1}^{n} (f_j(x_i) - \mu_{a_j})^2</tex> | ||
| − | + | На вход алгоритму подаётся выборка <tex>X^m = \{ x_1, \dots, x_m \}</tex> и количество кластеров <tex>K = |Y|</tex>. | |
| − | |||
| − | На | ||
| − | |||
| − | |||
| − | + | На выходе получаем центры кластеров <tex>\mu_a</tex> для кластеров <tex>a \in Y</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | <tex>\mu_a := init(X^m)</tex> <font color="gray"># Инициализируем произвольно начальное приближение для центров кластеров <tex>a \in Y</tex></font>. (Можно наиболее удалённые друг от друга объекты выборки) |
| − | + | <tex>A := [ -1 \: | \: for \: x_i \in X^m ]</tex> <font color="gray"># Инициализируем массив отображений из объектов выборки в их кластеры</font> | |
| − | + | <tex>changed := True</tex> | |
| − | < | + | <font color="blue"><tex>while</tex></font> <tex>changed</tex>: <font color="gray"># Повторяем пока <tex>A_i</tex> изменяются</font> |
| − | + | <tex>changed := False</tex> | |
| + | <font color="blue"><tex>for</tex></font> <tex>x_i \in X^m</tex>: <font color="gray"># Относим каждый <tex>x_i</tex> к ближайшему центру</font> | ||
| + | <tex>A_{i, old} := A_i</tex> | ||
| + | <tex>A_i := arg \min_{a \in Y} ||x_i - \mu_a||</tex> | ||
| + | <font color="blue"><tex>if</tex></font> <tex>A_i \neq A_{i, old}</tex>: | ||
| + | <tex>changed := True</tex> | ||
| + | <font color="blue"><tex>for</tex></font> <tex>a \in Y</tex>: <font color="gray"># Вычисляем новые положения центров</font> | ||
| + | <tex>\mu_a := \frac{\sum_{i = 1}^{m}[A_i = a] x_i}{\sum_{i = 1}^{m}[A_i = a]}</tex> | ||
| + | <font color="blue"><tex>return</tex></font> <tex>\mu_a, \: A</tex> <font color="gray"># Возвращаем центры кластеров и распределение по ним объектов выборки</font> | ||
| − | + | === DBSCAN === | |
| − | + | Основная идея метода заключается в том, что алгоритм разделит заданный набор точек в некотором пространстве на группы точек, которые лежат друг от друга на большом расстоянии. Объекты, которые лежат отдельно от скоплений с большой плотностью, будут помечены как шумовые. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | На вход алгоритму подаётся набор точек, параметры <tex>\epsilon</tex> (радиус окружности) и <tex>m</tex> (минимальное число точек в окрестности). Для выполнения кластеризации потребуется поделить точки на четыре вида: основные точки, прямо достижимые, достижимые и шумовые. | |
| − | + | * Точка является ''основной'', если в окружности с центром в этой точке и радиусом <tex>\epsilon</tex> находится как минимум <tex>m</tex> точек. | |
| + | * Точка <tex>a</tex> является ''прямо достижимой'' из основной точки <tex>b</tex>, если <tex>a</tex> находится на расстоянии, не большем <tex>{\epsilon}</tex> от точки <tex>b</tex>. | ||
| + | * Точка <tex>a</tex> является ''достижимой'' из <tex>b</tex>, если существует путь <tex>p_1, \dots, p_n</tex> с <tex>p_1 = a</tex> и <tex>p_n = b</tex>, где каждая точка <tex>p_{i+1}</tex> прямо достижима из точки <tex>p_i</tex> . | ||
| + | * Все остальные точки, которые не достижимы из основных точек, считаются ''шумовыми''. | ||
| − | + | Основная точка вместе со всеми достижимыми из нее точками формирует ''кластер''. В кластер будут входить как основные, так и неосновные точки. Таким образом, каждый кластер содержит по меньшей мере одну основную точку. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Алгоритм начинается с произвольной точки из набора, которая еще не просматривалась. Для точки ищется <tex>{\epsilon}</tex>-окрестность. Если она не содержит как минимум <tex>m</tex> точек, то помечается как шумовая, иначе образуется кластер <tex>K</tex>, который включает все точки из окрестности. Если точка из окрестности уже является частью другого кластера <tex>C_j</tex>, то все точки данного кластера добавляются в кластер <tex>K</tex>. Затем выбирается и обрабатывается новая, не посещённая ранее точка, что ведёт к обнаружению следующего кластера или шума. | |
| − | |||
| − | |||
| − | <tex> | ||
| − | |||
| − | + | На выходе получаем разбиение на кластеры и шумовые объекты. Каждый из полученных кластеров <tex>C_j</tex> является непустым множеством точек и удовлетворяет двум условиям: | |
| + | * Любые две точки в кластере попарно связаны (то есть найдется такая точка в кластере, из которой достижимы обе этих точки). | ||
| + | * Если точка достижима из какой-либо точки кластера, то она принадлежит кластеру. | ||
| − | + | Рассмотрим код: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Пусть для каждого <tex>x \in X^m</tex> имеем посчитанной его <tex>\epsilon</tex>-окрестность <tex>U_{\epsilon}(x) = \{x' \in X^m \: | \: \rho(x, x') \lt \epsilon\}</tex>. | |
| − | === | + | <tex>U := X^m</tex> <font color="gray"># Непомеченные объекты</font> |
| − | + | <tex>A := [ -1 \: | \: for \: x_i \in X^m ]</tex> <font color="gray"># Инициализируем массив отображений из объектов выборки в их кластеры</font> | |
| − | + | <tex>a := 0</tex> <font color="gray"># Количество кластеров</font> | |
| − | + | <font color="blue"><tex>while</tex></font> <tex>U \neq \varnothing</tex>: <font color="gray"># Пока в выборке есть непомеченные объекты</font> | |
| + | <tex>x := rand(U)</tex> <font color="gray"># Берём случайную непомеченную точку</font> | ||
| + | <font color="blue"><tex>if</tex></font> <tex>|U_{\epsilon}(x) < m|</tex>: | ||
| + | <tex>mark[x]</tex> <tex>:=</tex> "<tex>noise</tex>" <font color="gray"># Пометим <tex>x</tex> как, возможно, шумовой</font> | ||
| + | <font color="blue"><tex>else</tex></font>: | ||
| + | <tex>K := U_{\epsilon}(x)</tex> | ||
| + | <tex>a := a + 1</tex> <font color="gray"># Создадим новый кластер K</font> | ||
| + | <font color="blue"><tex>for</tex></font> <tex>x' \in K</tex>: | ||
| + | <font color="blue"><tex>if</tex></font> <tex>x' \in U</tex> || <tex>mark[x']</tex> <tex>==</tex> "<tex>noise</tex>": <font color="gray"># Если <tex>x'</tex> не помечен или помечен как шумовой</font> | ||
| + | <font color="blue"><tex>if</tex></font> <tex>|U_{\epsilon}(x')| \geq m</tex>: | ||
| + | <tex>mark[x'] :=</tex> "<tex>interior</tex>" <font color="gray"># Пометим <tex>x'</tex> как внутренний кластера <tex>K</tex></font> | ||
| + | <tex>K := K \cup U_{\epsilon}(x')</tex> <font color="gray"># Добавим вместе с <tex>x'</tex> всю его окрестность</font> | ||
| + | <font color="blue"><tex>else</tex></font>: | ||
| + | <tex>mark[x'] :=</tex> "<tex>frontier</tex>" <font color="gray"># Пометим <tex>x'</tex> как граничный кластера <tex>K</tex></font> | ||
| + | <font color="blue"><tex>for</tex></font> <tex>x_i \in K</tex>: | ||
| + | <tex>A_i := a</tex> | ||
| + | <tex>U := U \setminus K</tex> | ||
| + | <font color="blue"><tex>return</tex></font> <tex>a, \: A, \: mark</tex> <font color="gray"># Возвращаем количество кластеров, распределение по кластерам и метки объектов (внутренние, граничные или шумовые)</font> | ||
| − | + | DBSCAN находит практическое применение во многих реальных задачах, например, в маркетинге: необходимо предложить покупателю релевантный товар, который подойдет под его заказ. Выбрать такой товар можно, если посмотреть на похожие заказы других покупателей {{---}} в таком случае похожие заказы образуют кластер вещей, которые часто берут вместе. Похожим образом с помощью DBSCAN можно исследовать и находить общие интересы людей, делить их на социальные группы, моделировать поведение посетителей сайта. Алгоритм также может использоваться для [[Сегментация изображений|сегментации изображений]]. | |
| − | === | + | == Пример кода == |
| − | + | === Пример на языке R === | |
| − | + | {{Main|Примеры кода на R}} | |
| − | + | Для реализации алгоритма ''k-средних'' используется пакет <code>ClusterR</code>. В нем реализовано 2 функции: <code>KMeans_arma()</code> и <code>KMeans_rcpp()</code>. В примере далее рассмотрена реализация с использованием функции <code>KMeans_arma()</code>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <font color="gray"># importing package and its' dependencies</font> | |
| − | <font color= | + | library(ClusterR) |
| − | + | ||
| − | + | <font color="gray"># reading data</font> | |
| − | + | data <- read.csv(<font color="green">"data.csv"</font>) | |
| − | < | + | |
| − | <font color= | + | <font color="gray"># evaluating model</font> |
| − | + | model <- KMeans_arma(data, <font color="#660099">clusters</font> = <font color="blue">2</font>, <font color="#660099">n_iter</font> = <font color="blue">10</font>, <font color="#660099">seed_mode</font> = <font color="green">"random_subset"</font>, | |
| − | + | <font color="#660099">verbose</font> = T, <font color="#660099">CENTROIDS</font> = NULL) | |
| − | < | + | |
| − | <font color= | + | <font color="gray"># predicting results</font> |
| − | + | predictions <- predict_KMeans(test_data, model) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <font color= | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == См. также == | |
| + | * [[Оценка_качества_в_задаче_кластеризации|Оценка качества в задаче кластеризации]] | ||
| + | * [[EM-алгоритм|EM-алгоритм]] | ||
| + | * [[Иерархическая_кластеризация|Иерархическая кластеризация]] | ||
| + | * [[k-средних|<tex>\mathrm{k}</tex>-средних]]<sup>[на 28.01.18 не создан]</sup> | ||
== Примечания == | == Примечания == | ||
| Строка 187: | Строка 231: | ||
* [https://en.wikipedia.org/wiki/Cluster_analysis Wikipedia {{---}} Cluster analysis] | * [https://en.wikipedia.org/wiki/Cluster_analysis Wikipedia {{---}} Cluster analysis] | ||
* [http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BB%D0%B0%D1%81%D1%82%D0%B5%D1%80%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F MachineLearning {{---}} Кластеризация] | * [http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BB%D0%B0%D1%81%D1%82%D0%B5%D1%80%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F MachineLearning {{---}} Кластеризация] | ||
| − | |||
| − | |||
* [http://www.machinelearning.ru/wiki/images/c/ca/Voron-ML-Clustering.pdf К.В.Воронцов Лекции по алгоритмам кластеризации и многомерного шкалирования] | * [http://www.machinelearning.ru/wiki/images/c/ca/Voron-ML-Clustering.pdf К.В.Воронцов Лекции по алгоритмам кластеризации и многомерного шкалирования] | ||
| − | * | + | * [https://www.cs.cornell.edu/home/kleinber/nips15.pdf Kleinberg J. An Impossibility Theorem for Clustering] |
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Кластеризация]] | ||
Текущая версия на 19:11, 4 сентября 2022
Кластеризация (англ. cluster analysis) — задача группировки множества объектов на подмножества (кластеры) таким образом, чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров по какому-либо критерию.
Задача кластеризации относится к классу задач обучения без учителя.
Содержание
Постановка задачи кластеризации
Пусть — множество объектов, — множество идентификаторов (меток) кластеров. На множестве задана функция расстояния между объектами . Дана конечная обучающая выборка объектов . Необходимо разбить выборку на подмножества (кластеры), то есть каждому объекту сопоставить метку , таким образом чтобы объекты внутри каждого кластера были близки относительно метрики , а объекты из разных кластеров значительно различались.
| Определение: |
| Алгоритм кластеризации — функция , которая любому объекту ставит в соответствие идентификатор кластера . |
Множество в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки объектов из обучающей выборки изначально не заданы, и даже может быть неизвестно само множество .
Решение задачи кластеризации объективно неоднозначно по ряду причин:
- Не существует однозначного критерия качества кластеризации. Известен ряд алгоритмов, осуществляющих разумную кластеризацию "по построению", однако все они могут давать разные результаты. Следовательно, для определения качества кластеризации и оценки выделенных кластеров необходим эксперт предметной области;
- Число кластеров, как правило, заранее не известно и выбирается по субъективным критериям. Даже если алгоритм не требует изначального знания о числе классов, конкретные реализации зачастую требуют указать этот параметр[1];
- Результат кластеризации существенно зависит от метрики. Однако существует ряд рекомендаций по выбору метрик для определенных классов задач.[2].
Число кластеров фактически является гиперпараметром для алгоритмов кластеризации. Подробнее про другие гиперпараметры и их настройку можно прочитать в статье[3].
Теорема невозможности Клейнберга
Для формализации алгоритмов кластеризации была использована аксиоматическая теория. Клейнберг постулировал три простых свойства в качестве аксиом кластеризации и доказал теорему, связывающую эти свойства.
| Определение: |
| Алгоритм кластеризации является масштабно инвариантным (англ. scale-invariant), если для любой функции расстояния и любой константы результаты кластеризации с использованием расстояний и совпадают. |
Первая аксиома интуитивно понятна. Она требует, чтобы функция кластеризации не зависела от системы счисления функции расстояния и была нечувствительна к линейному растяжению и сжатию метрического пространства обучающей выборки.
| Определение: |
| Полнота (англ. Richness). Множество результатов кластеризации алгоритма в зависимости от изменения функции расстояния должно совпадать со множеством всех возможных разбиений множества объектов . |
Вторая аксиома утверждает, что алгоритм кластеризации должен уметь кластеризовать обучающую выборку на любое фиксированное разбиение для какой-то функции расстояния .
| Определение: |
Функция расстояния является допустимым преобразованием функции расстояния , если
|
| Определение: |
| Алгоритм кластеризации является согласованным (англ. consistent), если результат кластеризации не изменяется после допустимого преобразования функции расстояния. |
Третья аксиома требует сохранения кластеров при уменьшении внутрикластерного расстояния и увеличении межкластерного расстояния.
Исходя из этих аксиом Клейнберг сформулировал и доказал теорему:
| Теорема (Клейнберга, о невозможности): |
Для множества объектов, состоящего из двух и более элементов, не существует алгоритма кластеризации, который был бы одновременно масштабно-инвариантным, согласованным и полным. |
Несмотря на эту теорему Клейнберг показал[4], что иерархическая кластеризация по методу одиночной связи с различными критериями останова удовлетворяет любым двум из трех аксиом.
Типология задач кластеризации
Типы входных данных
- Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками (англ. features). Признаки могут быть как числовыми, так и категориальными;
- Матрица расстояний между объектами. Каждый объект описывается расстоянием до всех объектов из обучающей выборки.
Вычисление матрицы расстояний по признаковому описанию объектов может быть выполнено бесконечным числом способов в зависимости от определения метрики между объектами. Выбор метрики зависит от обучающей выборки и поставленной задачи.
Цели кластеризации
- Классификация объектов. Попытка понять зависимости между объектами путем выявления их кластерной структуры. Разбиение выборки на группы схожих объектов упрощает дальнейшую обработку данных и принятие решений, позволяет применить к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»). В данном случае стремятся уменьшить число кластеров для выявления наиболее общих закономерностей;
- Сжатие данных. Можно сократить размер исходной выборки, взяв один или несколько наиболее типичных представителей каждого кластера. Здесь важно наиболее точно очертить границы каждого кластера, их количество не является важным критерием;
- Обнаружение новизны (обнаружение шума). Выделение объектов, которые не подходят по критериям ни в один кластер. Обнаруженные объекты в дальнейшем обрабатывают отдельно.
Методы кластеризации
- Графовые алгоритмы кластеризации. Наиболее примитивный класс алгоритмов. В настоящее время практически не применяется на практике;
- Вероятностные алгоритмы кластеризации. Каждый объект из обучающей выборки относится к каждому из кластеров с определенной степенью вероятности:
- Иерархические алгоритмы кластеризации. Упорядочивание данных путем создания иерархии вложенных кластеров;
- Алгоритм -средних[на 28.01.19 не создан] (англ. -means). Итеративный алгоритм, основанный на минимизации суммарного квадратичного отклонения точек кластеров от центров этих кластеров;
- Распространение похожести (англ. affinity propagation). Распространяет сообщения о похожести между парами объектов для выбора типичных представителей каждого кластера;
- Сдвиг среднего значения (англ. mean shift). Выбирает центроиды кластеров в областях с наибольшей плотностью;
- Спектральная кластеризация (англ. spectral clustering). Использует собственные значения матрицы расстояний для понижения размерности перед использованием других методов кластеризации;
- Основанная на плотности пространственная кластеризация для приложений с шумами (англ. Density-based spatial clustering of applications with noise, DBSCAN). Алгоритм группирует в один кластер точки в области с высокой плотностью. Одиноко расположенные точки помечает как шум.
Меры качества кластеризации
Для оценки качества кластеризации задачу можно переформулировать в терминах задачи дискретной оптимизации. Необходимо так сопоставить объектам из множества метки кластеров, чтобы значение выбранного функционала качества приняло наилучшее значение. В качестве примера, стремятся достичь минимума среднего внутрикластерного расстояния или максимума среднего межкластерного расстояния .
Подробнее про меры качества можно прочитать в статье оценка качества в задаче кластеризации.
Применение
Биология и биоинформатика
- В области экологии кластеризация используется для выделения пространственных и временных сообществ организмов в однородных условиях;
- Кластерный анализ используется для группировки схожих геномных последовательностей в семейство генов, которые являются консервативными структурами для многих организмов и могут выполнять схожие функции;
- Кластеризация помогает автоматически определять генотипы по различным частям хромосом;
- Алгоритмы применяются для выделения небольшого числа групп генетических вариации человеческого генома.
Медицина
- Используется в позитронно-эмиссионной томографии для автоматического выделения различных типов тканей на трехмерном изображении;
- Применяется для выявления шаблонов устойчивости к антибиотикам; для классификации антибиотиков по типу антибактериальной активности.
Маркетинг
Кластеризация широко используется при изучении рынка для обработки данных, полученных из различных опросов. Может применяться для выделения типичных групп покупателей, разделения рынка для создания персонализированных предложений, разработки новых линий продукции.
Интернет
- Выделение групп людей на основе графа связей в социальных сетях;
- Повышение релевантности ответов на поисковые запросы путем группировки веб-сайтов по смысловым значениям поискового запроса.
Компьютерные науки
- Кластеризация используется в сегментации изображений для определения границ и распознавания объектов;
- Кластерный анализ применяется для определения образовавшихся популяционных ниш в ходе работы эволюционных алгоритмов для улучшения параметров эволюции;
- Подбор рекомендаций для пользователя на основе предпочтений других пользователей в данном кластере;
- Определение аномалий путем построения кластеров и выявления неклассифицированных объектов.
Псевдокод некоторых алгоритмов кластеризации
Метод K-средних (Алгоритм Ллойда)
Основная идея заключается в том, что на каждой итерации перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем объекты снова разбиваются на кластеры в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике. Алгоритм завершается, когда на какой-то итерации не происходит изменения внутрикластерного расстояния.
Алгоритм минимизирует сумму квадратов внутрикластерных расстояний:
На вход алгоритму подаётся выборка и количество кластеров .
На выходе получаем центры кластеров для кластеров .
# Инициализируем произвольно начальное приближение для центров кластеров . (Можно наиболее удалённые друг от друга объекты выборки) # Инициализируем массив отображений из объектов выборки в их кластеры : # Повторяем пока изменяются : # Относим каждый к ближайшему центру : : # Вычисляем новые положения центров # Возвращаем центры кластеров и распределение по ним объектов выборки
DBSCAN
Основная идея метода заключается в том, что алгоритм разделит заданный набор точек в некотором пространстве на группы точек, которые лежат друг от друга на большом расстоянии. Объекты, которые лежат отдельно от скоплений с большой плотностью, будут помечены как шумовые.
На вход алгоритму подаётся набор точек, параметры (радиус окружности) и (минимальное число точек в окрестности). Для выполнения кластеризации потребуется поделить точки на четыре вида: основные точки, прямо достижимые, достижимые и шумовые.
- Точка является основной, если в окружности с центром в этой точке и радиусом находится как минимум точек.
- Точка является прямо достижимой из основной точки , если находится на расстоянии, не большем от точки .
- Точка является достижимой из , если существует путь с и , где каждая точка прямо достижима из точки .
- Все остальные точки, которые не достижимы из основных точек, считаются шумовыми.
Основная точка вместе со всеми достижимыми из нее точками формирует кластер. В кластер будут входить как основные, так и неосновные точки. Таким образом, каждый кластер содержит по меньшей мере одну основную точку.
Алгоритм начинается с произвольной точки из набора, которая еще не просматривалась. Для точки ищется -окрестность. Если она не содержит как минимум точек, то помечается как шумовая, иначе образуется кластер , который включает все точки из окрестности. Если точка из окрестности уже является частью другого кластера , то все точки данного кластера добавляются в кластер . Затем выбирается и обрабатывается новая, не посещённая ранее точка, что ведёт к обнаружению следующего кластера или шума.
На выходе получаем разбиение на кластеры и шумовые объекты. Каждый из полученных кластеров является непустым множеством точек и удовлетворяет двум условиям:
- Любые две точки в кластере попарно связаны (то есть найдется такая точка в кластере, из которой достижимы обе этих точки).
- Если точка достижима из какой-либо точки кластера, то она принадлежит кластеру.
Рассмотрим код:
Пусть для каждого имеем посчитанной его -окрестность .
# Непомеченные объекты # Инициализируем массив отображений из объектов выборки в их кластеры # Количество кластеров : # Пока в выборке есть непомеченные объекты # Берём случайную непомеченную точку : "" # Пометим как, возможно, шумовой : # Создадим новый кластер K : || "": # Если не помечен или помечен как шумовой : "" # Пометим как внутренний кластера # Добавим вместе с всю его окрестность : "" # Пометим как граничный кластера : # Возвращаем количество кластеров, распределение по кластерам и метки объектов (внутренние, граничные или шумовые)
DBSCAN находит практическое применение во многих реальных задачах, например, в маркетинге: необходимо предложить покупателю релевантный товар, который подойдет под его заказ. Выбрать такой товар можно, если посмотреть на похожие заказы других покупателей — в таком случае похожие заказы образуют кластер вещей, которые часто берут вместе. Похожим образом с помощью DBSCAN можно исследовать и находить общие интересы людей, делить их на социальные группы, моделировать поведение посетителей сайта. Алгоритм также может использоваться для сегментации изображений.
Пример кода
Пример на языке R
Для реализации алгоритма k-средних используется пакет ClusterR. В нем реализовано 2 функции: KMeans_arma() и KMeans_rcpp(). В примере далее рассмотрена реализация с использованием функции KMeans_arma().
# importing package and its' dependencies
library(ClusterR)
# reading data
data <- read.csv("data.csv")
# evaluating model
model <- KMeans_arma(data, clusters = 2, n_iter = 10, seed_mode = "random_subset",
verbose = T, CENTROIDS = NULL)
# predicting results
predictions <- predict_KMeans(test_data, model)
См. также
- Оценка качества в задаче кластеризации
- EM-алгоритм
- Иерархическая кластеризация
- -средних[на 28.01.18 не создан]
Примечания
- ↑ scikit-learn — Clustering
- ↑ Cornwell, B. (2015). Linkage Criteria for Agglomerative Hierarchical Clustering. Social Sequence Analysis, 270–274
- ↑ Shalamov Viacheslav, Valeria Efimova, Sergey Muravyov, and Andrey Filchenkov. "Reinforcement-based Method for Simultaneous Clustering Algorithm Selection and its Hyperparameters Optimization." Procedia Computer Science 136 (2018): 144-153.
- ↑ Kleinberg J. An Impossibility Theorem for Clustering
- ↑ scikit-learn — Comparing different clustering algorithms on toy datasets