Коды Грея — различия между версиями
Godless (обсуждение | вклад) |
Godless (обсуждение | вклад) (й) |
||
| Строка 73: | Строка 73: | ||
Таким образом, шаг индукции доказан, следовательно, теорема верна. | Таким образом, шаг индукции доказан, следовательно, теорема верна. | ||
}} | }} | ||
| + | |||
| + | == Специальные типы кодов Грея == | ||
| + | === Сбалансированный Код Грея === | ||
| + | |||
| + | === Код Беккета-Грея === | ||
| + | Код Беккета-Грея был назван в честь ирландского писателя Сэмюэла Беккета, который интересовался симметрией. Его пьеса [http://en.wikipedia.org/wiki/Quad_(play) "Quad"] содержала в себе четырёх актёров и была разделена на 16 временных периодов. Каждый период заканчивался, когда один из четырёх актёров выходил на сцену или же, наоборот, появлялся на ней. Пьеса начиналась на пустой сцене, и Беккет хотел, чтобы каждое подмножество актёров появлялось ровно один раз. Ясно, что множество актёров, находящихся в данное время на сцене может быть представлено в виде 4-битного двоичного кода Грея. Беккет, однако, добавил дополнительное условие в сценарий: чтобы со сцены уходил всегда тот из актеров, кто находился на ней дольше остальных. Актёры могли быть представлены как [http://ru.wikipedia.org/wiki/FIFO FIFO очередь] так, что (из всех актёров на сцене) уходил всегда тот актёр, который был первым в этой очереди. Беккет не смог найти код Беккета-Грея для своей пьесы, да и вообще, исчерпывающее перечисление всех возможных последовательностей показывает, что такой код не существует для n = 4. Известно, что сегодня такие коды существуют для n = 2, 5, 6, 7, и 8, и не существуют для n = 3 или 4. | ||
| + | === Одноколейный Код Грея === | ||
== Применение == | == Применение == | ||
Версия 08:18, 27 ноября 2013
| Определение: |
| Код Грея (Gray code) — такое упорядочение -ичных (обычно двоичных) векторов, что соседние вектора отличаются только в одном разряде. |
Код назван в честь Фрэнка Грея, который в 1947-ом году получил патент на "отражённый двоичный код".
Содержание
Алгоритм построения
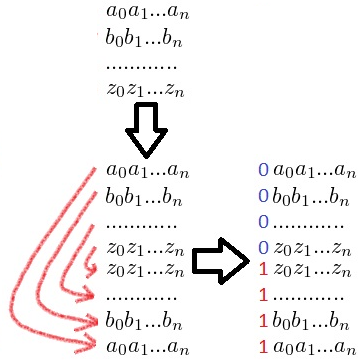
Существует несколько видов Кода Грея, самый простой из них — так называемый зеркальный двоичный Код Грея. Строится он так:
Для получения кода длины производится шагов. На первом шаге код имеет длину 1 и состоит из двух векторов (0) и (1). На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается "0", а ко второй "1". С каждым шагом длина векторов увеличивается на 1, а их количество — вдвое. Таким образом, количество векторов длины равно
Псевдокод
|
GrayCode — двумерный массив, в котором GrayCode[a, b] — -ый бит в -ом коде Грея. buildCode(n):
GrayCode[1, n] = 0
GrayCode[2, n] = 1 {построение кода длины 1}
p = 2 {p — количество уже имеющихся кодов}
for (i = 2, i <= n, i++):
p = p * 2
for (k = i + 1, k <= 2 * i, k++):
GrayCode[k] = GrayCode[p + 1 - k] {отражение имеющихся кодов}
GrayCode[k - i, n + 1 - i] = 0
GrayCode[k, n + 1 - i] = 1 {добавление 0 и 1 в начало}
|
Доказательство правильности работы алгоритма
По индукции:
- на первом шаге код отвечает условиям
- предположим, что код, получившийся на -ом шаге, является Кодом Грея
- тогда на шаге : первая половина кода будет корректна, так как она совпадает с кодом с шага за исключением добавленного последнего бита 0. Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит 1. На стыке: первые бит совпадают в силу зеркальности, последние различны по построению.
Таким образом, этот код — Код Грея. Индукционное предположение доказано, алгоритм работает верно.
Этот алгоритм можно обобщить и для -ичных векторов. Также известен алгоритм преобразования двоичного кода в Код Грея.
Существует ещё несколько видов Кода Грея — сбалансированный Код Грея, код Беккета-Грея, одноколейный Код Грея.
Явная формула для получения зеркального двоичного кода Грея
| Теорема: |
В двоичном зеркальном коде Грея -ый код может быть получен по формуле при нумерации кодов с нуля. |
| Доказательство: |
|
Для кода длиной 1 бит утверждение проверяется непосредственно. Пусть существует зеркальный двоичный код Грея длины , для которого выполнено, что для любого Обозначим за код длины , полученный из описанным выше алгоритмом. Тогда: Для любого Для любого , где , то есть
Таким образом, шаг индукции доказан, следовательно, теорема верна. |
Специальные типы кодов Грея
Сбалансированный Код Грея
Код Беккета-Грея
Код Беккета-Грея был назван в честь ирландского писателя Сэмюэла Беккета, который интересовался симметрией. Его пьеса "Quad" содержала в себе четырёх актёров и была разделена на 16 временных периодов. Каждый период заканчивался, когда один из четырёх актёров выходил на сцену или же, наоборот, появлялся на ней. Пьеса начиналась на пустой сцене, и Беккет хотел, чтобы каждое подмножество актёров появлялось ровно один раз. Ясно, что множество актёров, находящихся в данное время на сцене может быть представлено в виде 4-битного двоичного кода Грея. Беккет, однако, добавил дополнительное условие в сценарий: чтобы со сцены уходил всегда тот из актеров, кто находился на ней дольше остальных. Актёры могли быть представлены как FIFO очередь так, что (из всех актёров на сцене) уходил всегда тот актёр, который был первым в этой очереди. Беккет не смог найти код Беккета-Грея для своей пьесы, да и вообще, исчерпывающее перечисление всех возможных последовательностей показывает, что такой код не существует для n = 4. Известно, что сегодня такие коды существуют для n = 2, 5, 6, 7, и 8, и не существуют для n = 3 или 4.
Одноколейный Код Грея
Применение
- Использование кодов Грея основано прежде всего на том, что он минимизирует эффект ошибок при преобразовании аналоговых сигналов в цифровые (например, во многих видах датчиков).
- Коды Грея часто используются в датчиках-энкодерах. Их использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде.
- Коды Грея используются для кодирования номера дорожек в жёстких дисках.
- Код Грея можно использовать также и для решения задачи о Ханойских башнях:
Пусть n — количество дисков. Начнём с кода Грея длины n, состоящего из одних нулей (т.е. G(0)), и будем двигаться по кодам Грея (от G(i) переходить к G(i+1)). Поставим в соответствие каждому i-ому биту текущего кода Грея i-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита i как перемещение i-го диска. Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если n нечётно, то последовательность перемещений наименьшего диска имеет вид (где f — стартовый стержень, t — финальный стержень, r — оставшийся стержень), а если n чётно, то
- Коды Грея широко применяются в теории генетических алгоритмов для кодирования генетических признаков, представленных целыми числами.
- Коды Грея используются в Картах Карно (при передаче в карту переменные сортируются в Код Грея).
- Коды Грея также используются для связи систем с различной частотой работы.