| Определение: |
| [math]A=\{a_{1},a_{2}, \ldots ,a_{z}\}[/math], [math]B=\{b_{1},b_{2}, \ldots ,b_{z_{1}}\}[/math] — множества из различных объектов. [math]W=\{w_{1},w_{2}, \ldots ,w_{l}\}[/math] — количество объектов веса от [math]1[/math] до [math]l[/math] из [math]A[/math], а [math]U=\{u_{1},u_{2}, \ldots ,u_{l}\}[/math] — соответственно для [math]B[/math]. |
В дальнейшем, будем считать что нет объектов веса [math]0[/math], так как в противном случае существует бесконечное количество рассматриваемых комбинаторных объектов любого веса и подсчет теряет смысл, или подсчет сводится к рассматриваемому случаю. Отведем данный вес под пустое множество(то есть [math]w_{0}=1[/math]).
Последовательности (Seq)
| Определение: |
| [math]S=Seq(A)[/math] — множество всех последовательностей из элементов [math]A[/math]. [math]S_{n}[/math] — количество последовательностей веса [math]n[/math]. |
| Утверждение: |
[math]S_{n}=\sum\limits_{i=1}^{n} w_{i} S_{n-i}[/math]. Причем [math]S_{0} = 1[/math]. |
| [math]\triangleright[/math] |
|
[math]S_{0} = 1[/math], так как есть единственный способ составить пустую последовательность.
Докажем по индукции.
База [math]n = 1[/math].
- [math]S_{1}=w_{1} S_{0}=w_{1}[/math], что верно, так как единственный способ составить последовательность веса [math]1[/math] — это взять любой элемент веса [math]1[/math].
Переход.
- Пусть для [math]j \lt n[/math] верно. Докажем для [math]n[/math]. Возьмем произвольный элемент из [math]A[/math] веса [math]i \leqslant n[/math], и допишем его к последовательности элементов веса [math]n-i[/math]. Образуется новая последовательность веса [math]n[/math]. Причем никакая последовательность не будет учтена дважды, так как прежде не было последовательностей веса [math]n[/math] и ни к какой последовательности меньшего веса мы не добавляем один и тот же элемент дважды.
|
| [math]\triangleleft[/math] |
Подсчет битовых векторов длины [math]n[/math]
Пусть [math]A=\{0, 1\}[/math], [math]W=\{2, 0 \ldots 0\}[/math] [math]S=Seq(A)[/math] — множество всех битовых векторов.
Тогда, [math]S_{n}=\sum\limits\limits_{i=1}^{n} w_{i} S_{n-i}=2S_{n-1}=2^{n}[/math].
Подсчет Seq из маленьких и больших элементов
Пусть [math]A=\{1, 2\}[/math], [math]W=\{1, 1, 0 \ldots 0\}[/math], [math]S=Seq(A)[/math] — множество всех последовательностей из маленьких и больших элементов, [math]S_{1}=1[/math].
Тогда, [math]S_{n}=\sum\limits_{i=1}^{n} w_{i} S_{n-i}=S_{n-1}+S_{n-2}=F_{n}[/math], где [math]F_{n}[/math] — [math]n[/math]-ое число Фибоначчи [1].
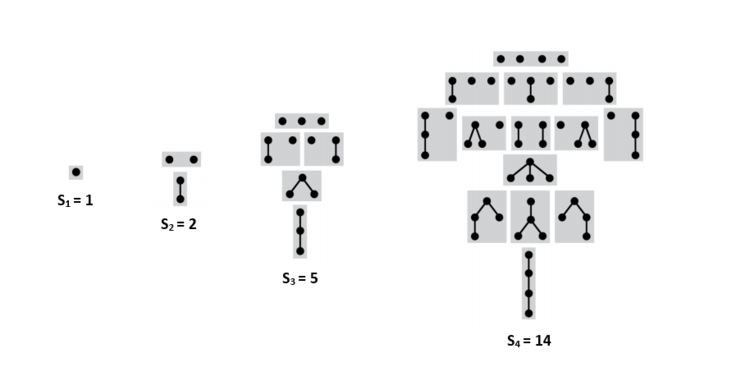
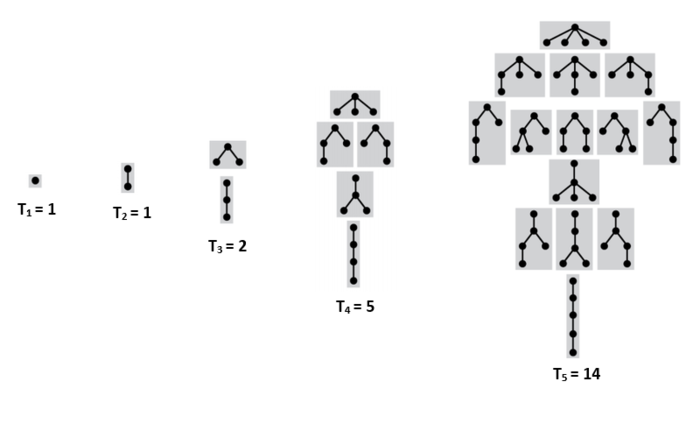
Подсчет подвешенных непомеченных деревьев с порядком на детях
Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]S=Seq(A)[/math] — множество всех последовательностей из данных деревьев. [math]S_{n}[/math] — количество последовательностей с суммарным количество вершин [math]n[/math]. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину, и подвесить к ней последовательность деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:
- [math]T_{n}=S_{n-1}[/math].
- [math]S_{n}=\sum\limits_{i=1}^{n} T_{i} S_{n-i}=\sum\limits_{i=1}^{n} S_{i-1} S_{n-i}=\sum\limits_{i=0}^{n-1} S_{i} S_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.
Множества (PSet)
| Определение: |
| [math]P=PSet(A)[/math] — множество всех множеств, составленных из элементов [math]A[/math]. [math]P_{n}[/math] — количество множеств суммарного веса [math]n[/math]. |
| Утверждение: |
[math]P_{n}=p_{n, n}[/math], где [math]p_{n, k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}}{i} p_{n-ik, k-1}[/math] — количество таких множеств, которые содержат объекты, вес которых не больше чем [math]k[/math]. Причем [math]p_{0, i} = 1[/math], а [math]p_{i, 0} = 0[/math], [math]i \ne 0[/math]. |
| [math]\triangleright[/math] |
|
[math]p_{0, i} = 1[/math], так как не набирать никакой вес есть один способ, а [math]p_{i, 0} = 0[/math], [math]i \ne 0[/math], так как нельзя набрать положительный вес из ничего.
Изначально у нас есть только пустое множество веса [math]0[/math]. Рассмотрим очередной этап вычисления [math]p_{n,k}[/math]. Для данных [math]n[/math] и [math]k[/math] у нас уже имеется множество, которое необходимо дополнить. Мы можем сделать это добавляя от [math]0[/math] до [math]\lfloor \frac{n}{k} \rfloor[/math] элементов веса [math]k[/math] (при условии, что столько различных элементов имеется) в данное множество. Выбрать нужное количество элементов можно с помощью сочетаний. Следовательно, у нас образуется новые множества, которые будет необходимо дополнить элементами веса меньше [math]k[/math] (чтобы избежать повторений) суммарного веса [math]n-ik[/math], где [math]i[/math] — количество элементов веса [math]k[/math] которое мы добавили в данное множество. Довольно легко заметить, что данные операции полностью соответствуют описанной выше формуле. |
| [math]\triangleleft[/math] |
Количество PSet из элементов 0 и 1
Пусть [math]A=\{0, 1\}[/math], [math]P=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math]. Тогда [math]P_{n}=p_{n, n}[/math], где [math]p_{n, k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}}{i}p_{n-ik, k-1}[/math].
- [math]P_{0}=p_{0, 0} = 1[/math].
- [math]P_{1}=p_{1, 1} = \binom{1}{0}p_{1, 0} + \binom{2}{1}p_{0, 0} = 2p_{0, 0} = 2[/math].
- [math]P_{2}=p_{2, 2} = \binom{0}{0} p_{2, 1} + \binom{0}{1}p_{0, 1} = \binom{2}{0}p_{2, 0} + \binom{2}{1}p_{1, 0} + \binom{2}{2}p_{0, 0}= p_{0, 0} = 1[/math].
- [math]{P_{3}=p_{3, 3} = \binom{0}{0}p_{3, 2} + \binom{0}{1} p_{0, 2} = \binom{0}{0}p_{3, 1} + \binom{0}{1} p_{0, 1} = \binom{2}{0}p_{3, 0} + \binom{2}{1}p_{2, 0} + \binom{2}{2} p_{1, 0} + \binom{2}{3} p_{0, 0}= 0}[/math].
- Для [math]n \gt 2[/math], [math]P_{n} = 0[/math] .
- [math]\{\}[/math]
- [math]\{0\}, \{1\}[/math]
- [math]\{0, 1\}[/math]
Количество разбиений на слагаемые
Пусть [math]A=\mathbb{N}[/math], [math]P=PSet(A)[/math] — множество всех разбиений на слагаемые, [math]W=\{1 \ldots 1\}[/math]. Тогда,
- [math]P_{n}=p_{n, n}[/math], где [math]p_{n, k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} p_{n-ik, k-1} = p_{n, k-1} + p_{n - k, k}[/math], что, как несложно заметить, соответствует формуле, полученной методом динамического программирования.
Мультимножества (MSet)
| Определение: |
| [math]M=MSet(A)[/math] — множество всех мультимножеств [2] из элементов [math]A[/math]. [math]M_{n}[/math] — количество мультимножеств из объектов суммарного веса [math]n[/math]. |
| Утверждение: |
[math]M_{n}=m_{n, n}[/math], где [math]m_{n, k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}+i-1}{i} m_{n-ik, k-1}[/math] — количество таких мультимножеств, которые содержат объекты, вес которых не больше чем [math]k[/math]. Причем [math]m_{0, i} = 1[/math], а [math]m_{i, 0} = 0[/math], [math]i \ne 0[/math]. |
| [math]\triangleright[/math] |
|
[math]m_{0, i} = 1[/math], так как не набирать никакой вес есть один способ, а [math]m_{i, 0} = 0[/math], [math]i \ne 0[/math], так как нельзя набрать положительный вес из ничего.
Рассуждения аналогичны рассуждениям [math]PSet[/math], однако теперь мы можем брать один и тот же элемент несколько раз. То есть для подсчета вместо обычных сочетаний нужно использовать сочетания с повторениями. |
| [math]\triangleleft[/math] |
Количество MSet из элементов 0 и 1
Пусть [math]A=\{0, 1\}[/math], [math]M=MSet(A)[/math] — множество всех мультимножеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math].
- Тогда, [math]M_{n}=m_{n, n}[/math], где [math]m_{n, k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}+i-1}{i}m_{n-ik, k-1}[/math]
- [math]M_{0}=m_{0, 0} = 1[/math].
- [math]M_{1}=m_{1, 1} = \binom{1}{0}m_{1, 0} + \binom{2}{1}m_{0, 0} = 2m_{0, 0} = 2[/math].
- [math]M_{2}=m_{2, 2} = \binom{0}{0}m_{2, 1} + \binom{0}{1} m_{0, 1} = \binom{1}{0}m_{2, 0} + \binom{2}{1}m_{1, 0} + \binom{3}{2}m_{0, 0}= 3m_{0, 0} = 3[/math].
- [math]{M_{3}=m_{3, 3} = \binom{0}{0}m_{3, 2} + \binom{0}{1} m_{0, 2} = \binom{0}{0}m_{3, 1} + \binom{0}{1} m_{0, 1} = \binom{1}{0}m_{3, 0} + \binom{2}{1}m_{2, 0} + \binom{3}{2}m_{1, 0} + \binom{4}{3}m_{0, 0}= 4m_{0, 0} = 4}[/math].
- [math]\{\}[/math]
- [math]\{0\}, \{1\}[/math]
- [math]\{0, 0\}, \{0, 1\}, \{1, 1\}[/math]
- [math]\{0, 0, 0\}, \{0, 0, 1\}, \{0, 1, 1\}, \{1, 1, 1\}[/math]
- [math]{M_{n}=m_{n, n} = \binom{0}{0}m_{n, n-1} + \binom{0}{1} m_{0, n-1} = \binom{0}{0}m_{n, n-2} + \binom{0}{1} m_{0, n-2} = \ldots = \binom{1}{0}m_{n, 0} + \binom{2}{1}m_{n - 1, 0} + \ldots + \binom{n}{n-1}m_{1, 0} + \binom{n+1}{n} m_{0,0} = (n + 1) m_{0,0} = n+1}[/math].
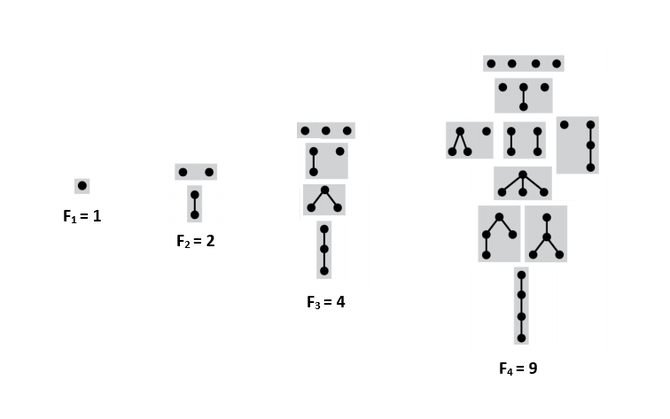
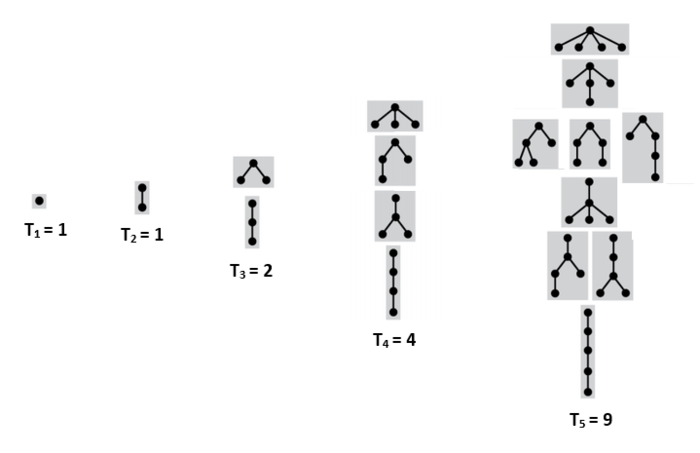
Подсчет подвешенных непомеченных деревьев без порядка на детях
Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]F=MSet(T)[/math] — множество всех лесов из данных деревьев, так как лес можно интерпретировать как мультимножество из деревьев. [math]F_{n}=f_{n,n}[/math] — количество лесов с суммарным количество вершин [math]n[/math]. [math]f_{n, k}[/math] — количество таких лесов из [math]n[/math] вершин, что деревья в них содержат не более чем [math]k[/math] вершин. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней лес деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:
- [math]T_{n}=F_{n-1}[/math].
- [math]F_{n}=f_{n, n}[/math].
- [math]f{n,k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{T_{k}+i-1}{i} s_{n-ik, k-1}[/math].
Количество таких деревьев с [math]n[/math] вершинами образуют последовательность [math] 1, 1, 2, 4, 9, 20, 48, 115, 286, 719, 1842, 4766, 12486, 32973, 87811, 235381, 634847 \ldots[/math] [3]
Пары (Pair)
| Определение: |
| [math]D=Pair(A, B)[/math] — множество всех пар объектов, составленных из элементов [math]A[/math] и [math]B[/math]. [math]D_{n}[/math] — количество пар из объектов суммарного веса [math]n[/math]. |
| Утверждение: |
[math]D_{n}=\sum\limits_{i=0}^{n}w_{i}u_{n-i}[/math]. |
| [math]\triangleright[/math] |
|
Чтобы составить пару веса [math]n[/math] нужно взять один элемент веса [math]0 \leqslant i \leqslant n[/math] из [math]A[/math] и элемент веса [math]n-i[/math] из [math]B[/math] , что полностью соответствует данной формуле. |
| [math]\triangleleft[/math] |
Количество подвешенных неполных двоичных деревьев
Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]D=Pair(T, T)[/math] — множество всех пар из данных деревьев. Чтобы получить двоичное дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней левого и правого сына с суммарным количеством вершин [math]n-1[/math]. Тогда:
- [math]T_{n}=D_{n-1}=\sum\limits_{i=0}^{n-1}T_{i}T_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.
Циклы (Cycle)
| Определение: |
| [math]C=Cycle(A)[/math] — множество всех циклов [4] из элементов [math]A[/math]. [math]C_{n}[/math] — количество циклов веса [math]n[/math]. |
| Утверждение: |
[math]C_{n}=\sum\limits_{s=1}^{n}c_{n, s}[/math], где [math]c_{n,s}=\sum\limits_{i=0}^{s-1}\dfrac{|St(\vec{i})|}{s}[/math], — количество циклов веса [math]n[/math] длины [math]s[/math], а [math]|St(\vec{i})|[/math] — количество стабилизаторов для циклического сдвига на [math]i[/math] . |
| [math]\triangleright[/math] |
|
Очевидно, что длина цикла веса [math]n[/math] может быть от [math]1[/math] до [math]n[/math]. Посмотрим сколько существует циклов каждой длины. Это можно сделать по лемме Бёрнсайда. |
| [math]\triangleleft[/math] |
| Лемма: |
Найдем [math]|St(\vec{i})|=z_{n,s,i}[/math] в общем случае. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Пусть [math]g=\mathrm{gcd}(s,i)[/math] — наибольший общий делитель[math](s, i)[/math]. Заметим, что в [math]i[/math]-ой перестановке на [math]j[/math]-ой позиции стоит элемент [math](i + j)\bmod s[/math]. Также, заметим, что элемент [math]a[/math] переходит в элемент [math]a + in[/math], где [math]i = 1, 2, \ldots k[/math]. Из этого следует, что длина цикла для [math]i[/math]-ой перестановки равна [math] \dfrac{\mathrm{lcm}(s, i)}{i} = \dfrac{s}{g}[/math], где [math]\mathrm{lcm}(s, i)[/math] — наименьшее общее кратное[math](s, i)[/math].
Также заметим, что если вес [math]n[/math] нельзя равномерно распределить по всей длине цикла, то стабилизатор равен [math]0[/math].
[math]z_{n, s, i} =
\left \{\begin{array}{ll} 0, & n \bmod \frac{s}{g} \neq 0 \\
b_{\frac{ng}{s}, g}, & n \bmod \frac{s}{g} = 0 \end{array} \right.
[/math]
Где [math]b_{n,k}[/math] — число способов упорядочить набор из [math]k[/math] элементов суммарного веса [math]n[/math] и
[math]b_{n,k}=\sum\limits_{i=1}^{n}w_{i}b_{n-i, k-1}[/math], причем [math]b_{n,1}=w_{n}[/math]. |
| [math]\triangleleft[/math] |
Задача об ожерельях
Решим данным способом задачу об ожерельях. Пусть необходимый вес [math]n[/math] — это количество бусинок, а [math]k[/math] — количество цветов. Причем каждая бусинка весит [math]1[/math]. То есть [math]W=\{k, 0 \ldots 0\}[/math].
[math]C_{n}=\sum\limits_{s=1}^{n}c_{n,s}=c_{n,n}[/math] так как невозможно набрать вес [math]n[/math] менее, чем [math]n[/math] бусинами при весе бусин [math]1[/math].
[math]c_{n,n}=\sum\limits_{i=0}^{n-1}\dfrac{|St(\vec{i})|}{n}=\dfrac{1}{n}\sum\limits_{i=0}^{s-1}|St(\vec{i})|=\dfrac{1}{n}\sum\limits_{i=0}^{s-1}b_{\mathrm{gcd}(n,i),\mathrm{gcd}(n,i)}[/math]. Поскольку все бусины имеют одинаковый вес [math]1[/math], то [math]b_{n,k} \neq 0[/math]
В итоге, [math]C_{n}=\dfrac{1}{n}\sum\limits_{i=0}^{s-1}k^{\mathrm{gcd}(n,i)}[/math].
Метод производящих функций
Такие большие группы часто анализируют с помощью производящих функций. Один из популярных методов — метод символов [5]. Он использует внутреннюю структуру объектов для получения производящих функций. В случае непомеченных объектов, как и в анализе в нашей статье, считается, что нет объектов нулевого веса. Иногда для удобства их добавляют, чтобы показать наличие одного пустого множества.
При непомеченных объектах рассмотренные классы имеют следующие производящие функции:
| [math]Seq(A)[/math] |
[math]\dfrac{1}{1-A(z)}[/math]
|
| [math]PSet(A)[/math] |
[math]\prod\limits_{n \geqslant 1}(1+z^{n})^{A_{n}}=\exp(-\sum\limits_{k \geqslant 1}\dfrac{(-1)^{k}A(z^{k})}{k})[/math]
|
| [math]MSet(A)[/math] |
[math]\prod\limits_{n \geqslant 1}\dfrac{1}{(1-z^{n})^{A_{n}}}=\exp(\sum\limits_{k \geqslant 1}\dfrac{A(z^{k})}{k})[/math]
|
| [math]Pair(A,B)[/math] |
[math]A(z)B(z)[/math]
|
| [math]Cycle(A)[/math] |
[math]\sum\limits_{n \geqslant 1}\dfrac{\phi(n)}{n}\ln\dfrac{1}{1 - A(z^n)}[/math], где [math]\phi(n)[/math] — функция Эйлера.
|
Однако порой некоторые комбинаторные классы удобнее обозначать как помеченные. Например, — помеченные графы. С помеченными объектами используется экспоненциальная производящая функция [6]. В данном случае для некоторых рассмотренных классов используются следующие производящие функции:
| [math]Seq(A)[/math] |
[math]\dfrac{1}{1-A(z)}[/math]
|
| [math]Pset(A)[/math] |
[math]\exp(A(z))[/math]
|
| [math]Pair(A,B)[/math] |
[math]A(z)B(z)[/math]
|
| [math]Cycle(A)[/math] |
[math]\ln\dfrac{1}{1-A(z)}[/math].
|
Ограниченные конструкции
Иногда в анализе необходимо ввести ограничение на количество компонентов. Такой случай обозначается нижним коэффициентом (например, [math]Seq_{k}(A)[/math] — [math]k[/math] компонентов).
Непосредственной формулой для производящих функций является диагональ [math]\Delta[/math] декартова произведения [7] [math]A \times A[/math], определяемая как [math]B \equiv \Delta(A \times A) : \{(a, a) \mid a \in A\}[/math]. Тогда имеет место соотношение [math]B(z)=A(z^{2})[/math].
Диагональная конструкция позволяет получить доступ к классу всех неупорядоченных пар из различных элементов из [math]A[/math], то есть к [math]P = PSet_{2}(A)[/math]. Прямое выражение выполняется следующим способом: неупорядоченная пара [math]\langle \alpha, \beta \rangle [/math] связана с двумя упорядоченными парами [math](\langle \alpha, \beta \rangle [/math] и [math]\langle \beta, \alpha \rangle )[/math], кроме тех случаев, когда [math]\alpha = \beta[/math], то есть когда пара лежит на диагонали декартова произведения. Другими словами, [math]PSet_{2}(A) + PSet_{2}(A) + \Delta(A \times A) \cong A \times A[/math].
Это, в свою очередь, означает что [math]2P(z) + A(z^{2}) = A(z)^{2}[/math]. Таким образом можно выразить [math]PSet_{2}(A)[/math]. Аналогично для [math]Seq_{2}(A)[/math], [math]MSet_{2}(A)[/math] и [math]Cycle_{2}(A)[/math]:
| [math]Seq_{2}(A)[/math] |
[math]A(z)^{2}[/math]
|
| [math]PSet_{2}(A)[/math] |
[math]\dfrac{A(z)^{2}}{2}-\dfrac{A(z^{2})}{2}[/math]
|
| [math]MSet_{2}(A)[/math] |
[math]\dfrac{A(z)^{2}}{2}+\dfrac{A(z^{2})}{2}[/math]
|
| [math]Cycle_{2}(A)[/math] |
[math]\dfrac{A(z)^{2}}{2}+\dfrac{A(z^{2})}{2}[/math]
|
Аналогичные рассуждения можно провести и для больших [math]k[/math], однако расчеты быстро становятся сложными. Классический способ исправления таких вопросов — теорема Пойа.
Однако в методе символов предлагается более глобальный подход, основанный на многомерных производящих функциях и использующий ряд Бюрмана-Лагранжа [8]. В общем случае, используя метод символов, производящие функции ограниченных конструкций можно подсчитать следующим способом:
| [math]Seq_{k}(A)[/math] |
[math]A(z)^{k}[/math]
|
| [math]PSet_{k}(A)[/math] |
[math][u^{k}]\exp(-\sum\limits_{i=1}^{k}\dfrac{(-1)^{i}u^{i}A(z^{i})}{i})[/math]
|
| [math]MSet_{k}(A)[/math] |
[math][u^{k}]\exp(\sum\limits_{i=1}^{k}\dfrac{u^{i}A(z^{i})}{i})[/math]
|
| [math]Cycle_{k}(A)[/math] |
[math][u^{k}]\sum\limits_{i \geqslant 1}\dfrac{\phi(i)}{i}\ln\dfrac{1}{1 - u^{i}A(z^i)}[/math], где [math]\phi(n)[/math] — функция Эйлера.
|
См.также
Примeчания
Источники информации



