Лемма о разрастании для КС-грамматик — различия между версиями
| Строка 7: | Строка 7: | ||
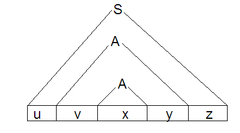
[[Файл:CS_lemma_conspect.PNG||left|240px|]] Грамматика любого контекстно-свободного языка может быть записана в [[Нормальная форма Хомского|нормальной форме Хомского (НФХ)]]. Пусть <tex>m</tex> — количество нетерминалов в грамматике языка <tex>L</tex>, записанной в НФХ. | [[Файл:CS_lemma_conspect.PNG||left|240px|]] Грамматика любого контекстно-свободного языка может быть записана в [[Нормальная форма Хомского|нормальной форме Хомского (НФХ)]]. Пусть <tex>m</tex> — количество нетерминалов в грамматике языка <tex>L</tex>, записанной в НФХ. | ||
Выберем <tex>n=2^{m+1}</tex>. Построим дерево разбора произвольного слова <tex>\omega</tex> длиной больше, чем <tex>n</tex>. Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка <tex>L</tex> записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова <tex>\omega</tex> не меньше <tex>m+1</tex>. | Выберем <tex>n=2^{m+1}</tex>. Построим дерево разбора произвольного слова <tex>\omega</tex> длиной больше, чем <tex>n</tex>. Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка <tex>L</tex> записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова <tex>\omega</tex> не меньше <tex>m+1</tex>. | ||
| + | |||
Рассмотрим самый длинный путь от вершины, соответствующей стартовому нетерминалу,до листа. В нем будет не менее <tex>m+1</tex> узлов, соответствующих нетерминалам. Следовательно, по принципу Дирихле найдется такой нетерминал <tex>A</tex>, который раскрывается в дереве разбора на этом пути дважды. Если таких путей и, следовательно, нетерминалов несколько, то выберем нетерминал максимальной глубины, у которого в поддереве содержится такой же нетерминал. Тогда в качестве <tex>x</tex> выберем кратчайшую строку из терминалов, которая выводится из <tex>A</tex>. Далее рассмотрим путь от предпоследнего повторения нетерминала <tex> A</tex> до последнего его вхождения в дерево. Если из вершины был сделан переход в левое поддерево, то строка, выведенная из правого поддерева, будет частью <tex>y</tex>. Аналогично из левых поддеревьев получаем <tex>v</tex>. Так как грамматика записана в НФХ, то либо <tex>v</tex>, либо <tex>y</tex> не будет пустой строкой, то есть условие <tex>|vy|>0</tex> выполнено. | Рассмотрим самый длинный путь от вершины, соответствующей стартовому нетерминалу,до листа. В нем будет не менее <tex>m+1</tex> узлов, соответствующих нетерминалам. Следовательно, по принципу Дирихле найдется такой нетерминал <tex>A</tex>, который раскрывается в дереве разбора на этом пути дважды. Если таких путей и, следовательно, нетерминалов несколько, то выберем нетерминал максимальной глубины, у которого в поддереве содержится такой же нетерминал. Тогда в качестве <tex>x</tex> выберем кратчайшую строку из терминалов, которая выводится из <tex>A</tex>. Далее рассмотрим путь от предпоследнего повторения нетерминала <tex> A</tex> до последнего его вхождения в дерево. Если из вершины был сделан переход в левое поддерево, то строка, выведенная из правого поддерева, будет частью <tex>y</tex>. Аналогично из левых поддеревьев получаем <tex>v</tex>. Так как грамматика записана в НФХ, то либо <tex>v</tex>, либо <tex>y</tex> не будет пустой строкой, то есть условие <tex>|vy|>0</tex> выполнено. | ||
Таким образом, <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} uvvAyyz \Rightarrow^{*} uv^{k}Ay^{k}z \Rightarrow^{*} uv^{k}xy^{k}z</tex>. | Таким образом, <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} uvvAyyz \Rightarrow^{*} uv^{k}Ay^{k}z \Rightarrow^{*} uv^{k}xy^{k}z</tex>. | ||
}} | }} | ||
Версия 21:35, 23 января 2012
| Лемма (о разрастании КС-грамматик): |
Пусть — контекстно-свободный язык над алфавитом , тогда существует такое , что для любого слова длины не меньше найдутся слова , для которых верно: и . |
| Доказательство: |
|
Грамматика любого контекстно-свободного языка может быть записана в нормальной форме Хомского (НФХ). Пусть — количество нетерминалов в грамматике языка , записанной в НФХ.
Выберем . Построим дерево разбора произвольного слова длиной больше, чем . Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова не меньше . Рассмотрим самый длинный путь от вершины, соответствующей стартовому нетерминалу,до листа. В нем будет не менее узлов, соответствующих нетерминалам. Следовательно, по принципу Дирихле найдется такой нетерминал , который раскрывается в дереве разбора на этом пути дважды. Если таких путей и, следовательно, нетерминалов несколько, то выберем нетерминал максимальной глубины, у которого в поддереве содержится такой же нетерминал. Тогда в качестве выберем кратчайшую строку из терминалов, которая выводится из . Далее рассмотрим путь от предпоследнего повторения нетерминала до последнего его вхождения в дерево. Если из вершины был сделан переход в левое поддерево, то строка, выведенная из правого поддерева, будет частью . Аналогично из левых поддеревьев получаем . Так как грамматика записана в НФХ, то либо , либо не будет пустой строкой, то есть условие выполнено. Таким образом, . |