В алгоритме Q-learning агент обучает функцию полезности действия [math]Q_{\theta}(s, a)[/math]. Стратегия агента [math]\pi_{\theta}(a|s)[/math] определяется согласно текущим значениям [math]Q(s, a)[/math], с использованием жадного, [math]\varepsilon[/math]-жадного или softmax подхода. Однако, существуют методы, которые позволяют оптимизировать стратегию [math]\pi_{\theta}(s|a)[/math] напрямую. Такие алгоритмы относятся к классу алгоритмов policy gradient.
Простой policy gradient алгоритм (REINFORCE)
Рассмотрим МППР, имеющий терминальное состояние: задача - максимизировать сумму всех выигрышей [math]R=r_0 + r_1+\cdots+r_T[/math], где T - шаг, на котором произошел переход в терминальное состояние.
Будем использовать букву [math]\tau[/math] для обозначения некоторого сценария - последовательности состояний и произведенных в них действий: [math]\tau = (s_1, a_1, s_2, a_2, ... s_T, a_T)[/math]. Будем обозначать сумму всех выигрышей, полученных в ходе сценария, как [math]R_{\tau} = \sum_{\tau} {r(s_t, a_t)}[/math].
Не все сценарии равновероятны. Вероятность реализации сценария зависит от поведения среды, которое задается вероятностями перехода между состояниями [math]p(s_{t+1}|s_{t}, a_{t})[/math] и распределением начальных состояний [math]p(s_1)[/math], и поведения агента, которое определяется его стохастической стратегией [math]\pi_{\theta}(a_t|s_t)[/math]. Вероятностное распределение над сценариями, таким образом, задается как
- [math]p_{\theta}(\tau) = p_{\theta}(s_1, a_1, ... s_T, a_T) = p(s_1) \prod_{t=1}^{T} {\pi_{\theta}(a_t|s_t) p(s_{t+1}|s_t, a_t)}[/math]
Будем максимизировать матожидание суммы полученных выигрышей:
- [math]J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ R_{\tau} \right] = \int {p_{\theta}(\tau) R_{\tau} d\tau}[/math]
Рассмотрим градиент оптимизируемой функции [math]\nabla_{\theta} J(\theta)[/math]:
- [math]\nabla_{\theta} J(\theta) = \int {\nabla_{\theta}p_{\theta}(\tau) R_{\tau} d\tau} [/math]
Считать градиент [math]\nabla_{\theta}p_{\theta}(\tau)[/math] непосредственно сложно, потому что что [math]p_{\theta}(\tau)[/math] - это большое произведение. Однако, так как
- [math]p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) = p_{\theta}(\tau) \frac{\nabla_{\theta}p_{\theta}(\tau)}{p_{\theta}(\tau)} = \nabla_{\theta}p_{\theta}(\tau)[/math]
, мы можем заменить [math]\nabla_{\theta}p_{\theta}(\tau)[/math] на [math]p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau)[/math]:
- [math]\nabla_{\theta} J(\theta) = \int {p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} d\tau} = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right][/math]
Рассмотрим [math]\log p_{\theta}(\tau)[/math]:
- [math] \log p_{\theta}(\tau) = \log \left( p(s_1) \prod_{t=1}^{T} {\pi_{\theta}(a_t|s_t) p(s_{t+1}|s_t, a_t)} \right) = \log p(s_1) + \sum_{t=1}^{T} {\left( \log \pi_{\theta}(a_t|s_t) + \log p(s_{t+1}|s_t, a_t) \right)} [/math]
Тогда:
- [math] \nabla_{\theta} \log p_{\theta}(\tau) = \underbrace{\nabla_{\theta} \log p(s_1)}_{=0} + \sum_{t=1}^{T} {\left( \nabla_{\theta} \log \pi_{\theta}(a_t|s_t) + \underbrace{\nabla_{\theta} \log p(s_{t+1}|s_t, a_t)}_{=0} \right)} = \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} [/math]
Подставляя в определение [math]\nabla_{\theta} J(\theta)[/math]:
- [math] \nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \right) R_{\tau} \right] [/math]
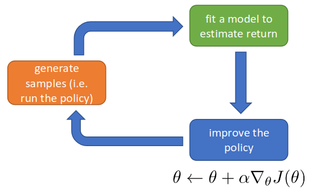
Схема алгоритма REINFORCE
Как мы можем подсчитать это матожидание? С помощью семплирования (метод Монте-Карло). Если у нас есть N уже известных сценариев [math]\tau^i = (s_1^i, a_1^i, ... s_{T^i}^i, a_{T^i}^i)[/math], то мы можем приблизить матожидание функции от сценария средним арифметическим этой функции по всему множеству сценариев:
- [math] \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N { \left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i)} \right) R_{\tau^i}} = \frac{1}{N} \sum_{i=1}^N { \left( \sum_{t=1}^{T^i} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i)} \right) \left( \sum_{t=1}^{T^i} { r(s_t^i, a_t^i) } \right)} [/math]
Таким образом, оптимизировать [math]J(\theta)[/math] можно с помощью следующего простого алгоритма (REINFORCE):
- Прогнать N сценариев [math]\tau_i[/math] со стратегией [math]\pi_{\theta}(a|s)[/math]
- Посчитать среднее арифметическое [math]\nabla_{\theta} J(\theta) \leftarrow \frac{1}{N} \sum_{i=1}^N { \left( \sum_{t=1}^{T^i} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i)} \right) \left( \sum_{t=1}^{T^i} { r(s_t^i, a_t^i) } \right)}[/math]
- [math] \theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)[/math]
Интуитивное объяснение принципа работы
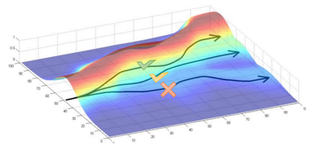
Иллюстрация выбора наилучшего сценария
[math]p_{\theta}(\tau)[/math] - это вероятность того, что будет реализован сценарий [math]\tau[/math] при условии параметров модели [math]\theta[/math], т. е. функция правдоподобия. Нам хочется увеличить правдоподобие "хороших" сценариев (обладающих высоким [math]R_{\tau}[/math]) и понизить правдоподобие "плохих" сценариев (с низким [math]R_{\tau}[/math]).
Взглянем еще раз на полученное определение градиента функции полного выигрыша:
- [math]\nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right][/math]
Двигаясь вверх по этому градиенту, мы повышаем логарифм функции правдоподобия для сценариев, имеющих большой положительный [math]R_{\tau}[/math].
Преимущества и недостатки policy gradient по сравнению с Q-learning
Преимущества:
- Легко обобщается на задачи с большим множеством действий, в том числе на задачи с непрерывным множеством действий.
- По большей части избегает конфликта между exploitation и exploration, так как оптимизирует напрямую стохастическую стратегию [math]\pi_{\theta}(a|s)[/math].
- Имеет более сильные гарантии сходимости: если Q-learning гарантированно сходится только для МППР с конечными множествами действий и состояний, то policy gradient, при достаточно точных оценках [math]\gt \nabla_{\theta} J(\theta)[/math] (т. е. при достаточно больших выборках сценариев), сходится к локальному оптимуму всегда, в том числе в случае бесконечных множеств действий и состояний, и даже для частично наблюдаемых Марковских процессов принятия решений (POMDP).
Недостатки:
- Очень низкая скорость работы -- требуется большое количество вычислений для оценки [math]\nabla_{\theta} J(\theta)[/math] по методу Монте-Карло, так как:
- для получения всего одного семпла требуется произвести [math]T[/math] взаимодействий со средой;
- случайная величина [math]\nabla_{\theta} \log p_{\theta}(\tau) R_{\tau}[/math] имеет большую дисперсию, так как для разных [math]\tau[/math] значения [math]R_{\tau}[/math] могут очень сильно различаться, поэтому для точной оценки [math]\nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right][/math] требуется много семплов;
- cемплы, собранные для предыдущих значений [math]\theta[/math], никак не переиспользуются на следующем шаге, семплирование нужно делать заново на каждом шаге градиентного спуска.
- В случае конечных МППР Q-learning сходится к глобальному оптимуму, тогда как policy gradient может застрять в локальном.
Далее мы рассмотрим способы улучшения скорости работы алгоритма.
Усовершенствования алгоритма
Опорные значения
Заметим, что если [math]b[/math] - константа относительно [math]\tau[/math], то
- [math]E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right] = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right] [/math]
, так как
- [math]E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) b \right] = \int {p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) b d\tau} = \int {\nabla_{\theta} p_{\theta}(\tau) b d\tau} = b \nabla_{\theta} \int {p_{\theta}(\tau) d\tau} = b \nabla_{\theta} 1 = 0[/math]
Таким образом, изменение [math]R_{\tau}[/math] на константу не меняет оценку [math]\nabla_{\theta} J(\theta)[/math]. Однако дисперсия [math] Var_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right][/math] зависит от [math]b[/math]:
- [math] Var_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right] = \underbrace{E_{\tau \sim p_{\theta}(\tau)} \left[ \left( \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right)^2 \right]}_{\text{depends on } b} - \underbrace{E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right]^2}_{= E \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right]^2} [/math]
, поэтому, регулируя [math]b[/math], можно достичь более низкой дисперсии, а значит, более быстрой сходимости Монте-Карло к истинному значению [math]\nabla_{\theta} J(\theta)[/math]. Значение [math]b[/math] называется опорным значением. Способы определения опорных значений будут рассмотрены далее.
Использование будущего выигрыша вместо полного выигрыша
Рассмотрим еще раз выражение для градиента полного выигрыша:
- [math] \nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \right) R_{\tau} \right] = E_{\tau \sim p_{\theta}(\tau)} \left[ \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \left( \sum_{t=1}^{T} {r(s_t, a_t)} \right) \right][/math]
Так как в момент времени [math]t[/math] от действия [math]a_t[/math] зависят только [math]r(s_{t'}, a_{t'})[/math] для [math] t' \leq t[/math], это выражение можно переписать как
- [math] \nabla_{\theta} J(\theta) \approx E_{\tau \sim p_{\theta}(\tau)} \left[ \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \underbrace{\left( \sum_{t'=t}^{T} {r(s_{t'}, a_{t'})} \right)}_{= Q_{\tau, t}} \right][/math]
Величина [math]Q_{\tau, t}[/math] -- будущий выигрыш (reward-to-go) на шаге [math]t[/math] в сценарии [math]\tau[/math]
Алгоритм Actor-Critic
Из предыдущего абзаца:
- [math]\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i) Q_{\tau_i, t} } [/math]
Здесь [math]Q_{\tau_i, t}[/math] -- это оценка будущего выигрыша из состояния [math]s_t^i[/math] при условии действия [math]a_t^i[/math], которая базируется только на одном сценарии [math]\tau_i[/math]. Это плохое приближение ожидаемого будущего выигрыша -- истинный ожидаемый будущий выигрыш выражается формулой
- [math] Q^{\pi}(s_t, a_t) = \sum_{t'=t}^{T} {E_{\pi_{\theta}} [r(s_{t'}, a_{t'}) | s_t, a_t] } [/math]
Также, в целях уменьшения дисперсии случайной величины, введем опорное значение для состояния [math]s_t[/math], которое назовем ожидаемой ценностью (value) этого состояния. Ожидаемая ценность состояния [math]s_t[/math] -- это ожидаемый будущий выигрыш при совершении некоторого действия в этом состоянии согласно стратегии [math]\pi_{\theta}(a|s)[/math]:
- [math] V^{\pi}(s_t) = E_{a_t \sim \pi_{\theta}(a_t | s_t)} [Q^{\pi}(s_t, a_t)] = \sum_{t'=t}^{T} {E_{\pi_{\theta}} [r(s_{t'}, a_{t'}) | s_t]}[/math]
Таким образом, вместо ожидаемого будущего выигрыша при оценке [math]\nabla_{\theta} J(\theta)[/math] будем использовать функцию преимущества (advantage):
- [math] A^{\pi}(s_t, a_t) = Q^{\pi}(s_t, a_t) - V^{\pi}(s_t) [/math]
Преимущество действия [math]a_t[/math] в состоянии [math]s_t[/math] -- это величина, характеризующая то, насколько выгоднее в состоянии [math]s_t[/math] выбрать именно действие [math]a_t[/math].
Итого:
- [math] \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i) A^{\pi}(s_t^i, a_t^i) } [/math]
Как достаточно точно и быстро оценить [math]A^{\pi}(s_t^i, a_t^i)[/math]? Сведем задачу к оценке [math]V^{\pi}(s_t)[/math]:
- [math] Q^{\pi}(s_t, a_t) = r(s_t, a_t) + E_{s_{t+1} \sim p(s_{t+1} | s_t, a_t)} [V^{\pi}(s_{t+1})] \approx r(s_t, a_t) + V^{\pi}(s_{t+1}) [/math]
- [math] A^{\pi}(s_t^i, a_t^i) = Q^{\pi}(s_t, a_t) - V^{\pi}(s_t) \approx r(s_t, a_t) + V^{\pi}(s_{t+1}) - V^{\pi}(s_t) [/math]
Теперь нам нужно уметь оценивать [math]V^{\pi}(s_t) = \sum_{t'=t}^{T} {E_{\pi_{\theta}} [r(s_{t'}, a_{t'}) | s_t] }[/math]. Мы можем делать это, опять же, с помощью метода Монте-Карло -- так мы получим несмещенную оценку. Но это будет работать не существенно быстрее, чем обычный policy gradient. Вместо этого заметим, что при фиксированных [math]s_t[/math] и [math]a_t[/math] выполняется:
- [math] V^{\pi}(s_t) = r(s_t, a_t) + V^{\pi}(s_{t+1})[/math]
Таким образом, если мы имеем некоторую изначальную оценку [math]V^{\pi}(s)[/math] для всех [math]s[/math], то мы можем обновлять эту оценку путем, аналогичным алгоритму Q-learning:
- [math] V^{\pi}(s_t) \leftarrow (1 - \beta) V^{\pi}(s_t) + \beta (r(s_t, a_t) + V^{\pi}(s_{t+1})) [/math]
Такой пересчет мы можем производить каждый раз, когда агент получает вознаграждение за действие. Так мы получим оценку ценности текущего состояния, не зависящуювы от выбранного сценария развития событий [math]\tau[/math], а значит, и оценка функции преимущества не будет зависеть от выбора конкретного сценария. Это сильно снижает дисперсию случайной величины [math]\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i) A^{\pi}(s_t^i, a_t^i)[/math], что делает оценку [math]\nabla_{\theta} J(\theta)[/math] достаточно точной даже в том случае, когда мы используем всего один сценарий для ее подсчета:
- [math]\nabla_{\theta} J(\theta) \approx \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t) A^{\pi}(s_t, a_t) }[/math]
На практике мы
Ссылки

