Обсуждение участника:SergeyBud — различия между версиями
SergeyBud (обсуждение | вклад) |
Shersh (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | '''HAT(Hashed Array Tree)''' {{---}} структура данных, объединяющая в себе некоторые возможности массивов, хэш-таблиц и деревьев. В действительности HAT {{---}} это эффективный способ реализовать массивы переменной длины, так как он предлагает хорошую производительность порядка <math>O(N)</math>, чтобы добавить <math>N</math> элементов к пустому массиву и требует всего лишь <math>O(\sqrt{N})</math> дополнительной памяти. | + | '''HAT(Hashed Array Tree)''' {{---}} структура данных, объединяющая в себе некоторые возможности массивов, хэш-таблиц и деревьев. В действительности HAT {{---}} это эффективный способ реализовать массивы переменной длины, так как он предлагает хорошую производительность порядка <math>O(N)</math>, чтобы добавить <math>N</math> элементов к пустому массиву, и требует всего лишь <math>O(\sqrt{N})</math> дополнительной памяти. |
==Значимость== | ==Значимость== | ||
Версия 14:42, 5 июня 2014
HAT(Hashed Array Tree) — структура данных, объединяющая в себе некоторые возможности массивов, хэш-таблиц и деревьев. В действительности HAT — это эффективный способ реализовать массивы переменной длины, так как он предлагает хорошую производительность порядка , чтобы добавить элементов к пустому массиву, и требует всего лишь дополнительной памяти.
Содержание
Значимость
Массивы переменной длины — наиболее естественная и удобная структура данных для многих приложений, так как они обеспечивают постоянное время доступа к их элементам. Однако при их реализации мы можем столкнуться с двумя основными проблемами: чрезмерное копирование элементов и использование памяти. HAT — реализация массива переменной длины, решающая обе проблемы и предоставляющая ряд преимуществ по сравнению со стандартными реализациями.
Устройство HAT
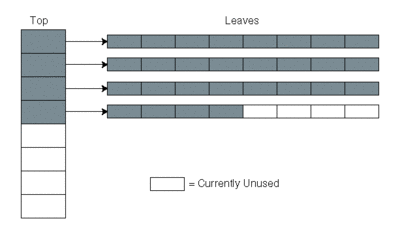
HAT состоит из главного массива указателей(top) и ряда листьев(leaf) (так же одномерные массивы), в которых хранятся элементы. Число указателей в главном массиве и число элементов в каждом листе равны между собой и являются степенями двойки.
Добавление элементов
Благодаря использованию степеней двойки, мы можем эффективно находить элементы в HAT, используя поразрядные операции.
topIndex(j) // Получить номер указателя в основном массиве return j >> power; leafIndex(j) // Получить номер листа return j & ((1<<power)-1); getHat(j) // Вернуть элемент HAT. Нет проверки на выход за пределы массива. return top[topIndex(j)][leafIndex(j)];
Чаще всего при добавлении элемента в одном из листьев (последнем незаполненном на данный момент) найдется свободное место, что позволит осуществить быструю вставку(). Реже мы столкнемся со случаем, когда необходимо создать новый лист. Достаточно всего лишь добавить указатель в свободную ячейку главного массива, что также позволит произвести вставку элемента за . Самый интересный случай — когда главный массив и все листья заполнены. Cначала вычислим нужный размер (массивы Top и Leaf имеют тот же самый размер, оба в степени 2), затем скопируем элементы в новую структуру HAT, освобождая старые листья и распределяя новые листья(размер листа изменился, а значит количество элементов в листе и количество используемых листьев так же изменится). Такой подход к расширению помогает избежать избыточного перекопирования, используемого во многих реализациях массивов переменной длины. Копировать элементы мы будем только тогда, когда главный массив полон(достигли соответствующей степени двойки). Например, для (k - натуральное число), общая сумма перекопирования будет равна 1+4+16+64+256+...+N. Воспользуемся тождеством: , тогда для нашего случая: , или около . Это означает, что среднее число дополнительных операций копирования - для последовательного добавления N элементов, а не .
Расход памяти
При перераспределении и копировании HAT использует меньше дополнительной памяти, чем в стандартных подходах. Самый плохой случай для HAT — размер элементов равен размеру указателей, и число элементов на один больше числа, при котором происходит расширение структуры(N=ResizeValue+1). Для этого случая значения приведены в таблице. Затраты доролнительной памяти в самом плохом случае — . Если последний лист будет половиной полного, то ожидаемая трата дополнительной памяти уменьшается до (top — главный массив, leaf — листья), а это все еще . Сравним с другими структурами, добавляющими элементы за . Например, отдельно связанные списки требуют O(N) дополнительной памяти (один указатель для каждого элемента).
Эффективность
Благодаря преимуществам, предоставляемыми HAT(так например вычисления адреса происходит приблизительно в 2 раза быстрее, чем в стандартном массиве C++), ее можно использовать в любых программах, требующих работу с массивами переменной длинны, где использование других структур данных (например списков) не удобно. На многих алгоритмах HAT работает значительно быстрее стандартных массивов, результаты тестов можно посмотреть здесь: [1]
Заключение
HAT — удобная структура данных переменной длины, позволяющая добавить N элементов за времени и требующая дополнительной памяти. HAT обеспечивает все стандартные возможности обычных массивов, включая произвольный доступ к элементам. Она поддерживает известный объем памяти для любого количества элементов и не требует специальной настройки для эффективной работы приложений. Таким образом, HAT предлагает ряд существенных преимуществ над другими реализациями массивов переменной длины.
Источники информации
- Википедия
- Cline, M.P. and G.A. Lomow, C++ FAQs, Reading, MA: Addison-Wesley, 1995.
- Cormen, T.H., C.E. Leiserson, and R.L. Rivest. Introduction to Algorithms, Cambridge, MA: MIT Press, 1990.