Обсуждение участницы:Анна
Содержание
Перечисления графов
Помеченные графы
| Определение: |
| Помеченный граф с вершинами — граф, у которого каждая вершина помечена целым числом от до . |
Более формально определить это понятие можно так: назовем распределением меток в графе с вершинами биекцию между множеством вершин графа и множеством . Тогда помеченным графом называется пара .
| Определение: |
| Два помеченных графа и изоморфны, если существует изоморфизм между и , сохраняющий распределение меток. |
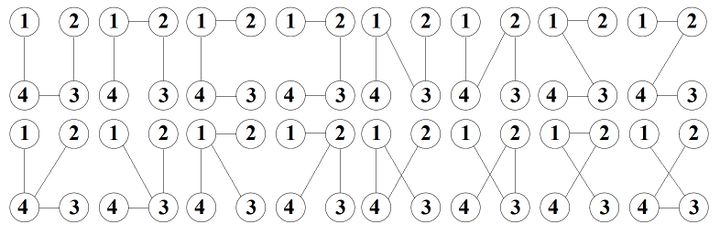
Все помеченные графы с тремя вершинами показаны на рисунке 1. различных графа с вершинами приводят к различным помеченным графам.
Для нахождения числа помеченных графов с вершинами нужно заметить, что каждое из возможных ребер либо принадлежит графу, либо нет.
| Теорема (1): |
Число помеченных графов с вершинами равно . |
Следовательно, число помеченных графов с ребрами равно .
| Теорема (Кэли): |
Число помеченных деревьев с вершинами равно . |
| Теорема (2): |
Данный граф можно пометить способами. |
| Доказательство: |
|
Приведем набросок доказательства. Пусть — группа подстановок, действующая на множестве . Для всякого элемента орбитой элемента называется подмножество множества , состоящее из всех элементов таких, что для некоторой подстановки из . Стабилизатором элемента называется подгруппа группы , состоящая из всех подстановок из , оставляющих элемент неподвижным. Теорема является следствием соотношения и его интерпретации в настоящем контексте. |
Рассмотрим пример. На рисунке 2 изображены все помеченные деревья с четырьмя вершинами. Всего их . Среди них изоморфны цепи и — графу . Порядок группы равен . Порядок группы . Так как , то имеем и .
Теорема перечисления Пойа
Пойа показал, как получить формулу, перечисляющую орбиты в соответствии с весами и зависящую от циклической структуры подстановок данной группы.
| Теорема: |
Пусть — группа подстановок, действующая на множестве с орбитами и — функция, приписывающая веса каждой орбите (весовая функция). Более того, определяется на так, что , если . Тогда сумма весов орбит равна . |
| Доказательство: |
| Уже упоминалось о том, что порядок группы равен для любого , где — стабилизатор элемента . Так как весовая функция постоянна на элементах данной орбиты, то справедливо равенство для каждой орбиты . Домножив второе равенство на первое и сократив, получаем . Суммируя по всем орбитам, находим , откуда непосредственно следует доказываемое соотношение. |
Как следствие из этой теоремы выведем традиционную формулу Бернсайда. Для подстановки через обозначим число циклов длины в её разложении в произведение непересекающихся циклов.
| Лемма (Бернсайд): |
Число орбит группы подстановок равно . |
| Доказательство: |
| Так как в доказательстве этой леммы мы не учитываем значения весовой функции, то , но и есть , то есть для получения исходной формулы нужно поделить обе части равенства на . |
Теорема Гуйя-Ури
Лемма о длине цикла в ориентированном графе
| Лемма (о длине цикла в ориентированном графе): |
Пусть — произвольный ориентированный граф и для каждой вершины выполняется . Если , то в графе существует простой цикл длины хотя бы . |
| Доказательство: |
| Рассмотрим путь максимальной длины . Из последней вершины выходит хотя бы ребро в вершины, отличные от . Так как путь максимальный, то продлить его нельзя, а значит, что из выходят ребра только в вершины, содержащиеся в пути . Пусть — вершина с наименьшим номером, в которую входит ребро из . Тогда во множество входят не менее ребер, выходящих из . То есть в это множестве хотя бы вершин. Значит, в цикле не менее вершины. |
Теорема Гуйя-Ури
| Теорема (Гуйя-Ури, Ghouila-Houri): |
Если — сильносвязный ориентированный граф c вершинами и для каждой выполняется , |
| Доказательство: |
| Будем доказывать теорему от противного. Предположим, что это не так. Очевидно, что условие теоремы выполняется при и . Тогда существует орсвязный граф с , который удовлетворяет условию и при этом не является гамильтоновым. Пусть — максимальный цикл в длины . По лемме о длине цикла и по предположению о том, что граф не является гамильтоновым, получаем соотношение . |