Оценка качества в задачах классификации и регрессии — различия между версиями
MuratOK (обсуждение | вклад) (→SMAPE, Symmetric MAPE (симметричная MAPE)) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 134 промежуточные версии 4 участников) | |||
| Строка 3: | Строка 3: | ||
== Оценки качества классификации == | == Оценки качества классификации == | ||
| − | === Сonfusion matrix | + | === Матрица ошибок (англ. Сonfusion matrix) === |
| − | Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — | + | Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок). |
Допустим, что у нас есть два класса <math>y = \{ 0, 1 \}</math> и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. | Допустим, что у нас есть два класса <math>y = \{ 0, 1 \}</math> и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. | ||
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика (<math>y = 1 </math>) можно рассматривать как "сигнал тревоги", сообщающий о возможных рисках. | Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика (<math>y = 1 </math>) можно рассматривать как "сигнал тревоги", сообщающий о возможных рисках. | ||
| Строка 18: | Строка 18: | ||
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой <math>y = 1 </math>, чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный - отрицательным (заемщик кредитоспособен <math>y = 0 </math>). Тогда возможны следующие исходы классификации: | Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой <math>y = 1 </math>, чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный - отрицательным (заемщик кредитоспособен <math>y = 0 </math>). Тогда возможны следующие исходы классификации: | ||
| − | * Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными ( | + | * Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются '''истинно-положительными''' ('''True Positive''' {{---}} '''TP'''). |
| − | * Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными ( | + | * Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются '''истинно отрицательными''' ('''True Negative''' {{---}} '''TN'''). |
| − | * Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными ( | + | * Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются '''ложно-положительными''' ('''False Positive''' {{---}} '''FP'''), а ошибка классификации называется '''ошибкой I рода'''. |
| − | * Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными ( | + | * Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются '''ложно-отрицательными''' ('''False Negative''' {{---}} '''FN'''), а ошибка классификации называется '''ошибкой II рода'''. |
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации: | Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации: | ||
| − | + | ||
| + | : {| class="wikitable" style="text-align: center" | ||
| + | | | ||
| + | |<math>y = 1</math> | ||
| + | |<math>y = 0</math> | ||
| + | |- | ||
| + | |<math>a ( x ) = 1</math> | ||
| + | |Истинно-положительный ('''True Positive — TP''') | ||
| + | |Ложно-положительный ('''False Positive — FP''') | ||
| + | |- | ||
| + | |<math>a ( x ) = 0</math> | ||
| + | |Ложно-отрицательный ('''False Negative — FN''') | ||
| + | |Истинно-отрицательный ('''True Negative — TN''') | ||
| + | |} | ||
Здесь <math>a ( x )</math> — это ответ алгоритма на объекте, а <math>y </math> — истинная метка класса на этом объекте. | Здесь <math>a ( x )</math> — это ответ алгоритма на объекте, а <math>y </math> — истинная метка класса на этом объекте. | ||
| − | Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). | + | Таким образом, ошибки классификации бывают двух видов: '''False Negative''' ('''FN''') и '''False Positive''' ('''FP'''). |
| − | Каждая строка в матрице ошибок представляет | + | '''P''' означает что классификатор определяет класс объекта как положительный ('''N''' {{---}} отрицательный). '''T''' значит что класс предсказан правильно (соответственно '''F''' {{---}} неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец {{---}} фактический класс. |
<font color="green"># код для матрицы ошибок</font> | <font color="green"># код для матрицы ошибок</font> | ||
| + | <font color="green">'''# Пример классификатора, способного проводить различие между всего лишь двумя</font> | ||
| + | <font color="green">'''# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST</font> | ||
| + | '''import''' numpy '''as''' np | ||
| + | '''from''' sklearn.datasets '''import''' fetch_openml | ||
| + | '''from''' sklearn.model_selection '''import''' cross_val_predict | ||
'''from''' sklearn.metrics '''import''' confusion_matrix | '''from''' sklearn.metrics '''import''' confusion_matrix | ||
| − | ''' | + | '''from''' sklearn.linear_model '''import''' SGDClassifier |
| − | '' | + | mnist = fetch_openml('mnist_784', version=1) |
| − | + | X, y = mnist["data"], mnist["target"] | |
| − | + | y = y.astype(np.uint8) | |
| − | + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | |
| + | y_train_5 = (y_train == 5) <font color="green"># True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | sgd_clf = SGDClassifier(random_state=42)<font color="green"> # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD)</font> | ||
| + | sgd_clf.fit(X_train, y_train_5) <font color="green"># обучаем классификатор распозновать пятерки на целом обучающем наборе</font> | ||
| + | <font color="green"># Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями</font> | ||
| + | y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) | ||
| + | print(confusion_matrix(y_train_5, y_train_pred)) | ||
| + | <font color="green"># array([[53892, 687], | ||
| + | # [ 1891, 3530]])</font> | ||
| + | Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла): | ||
| − | === | + | '''import''' numpy '''as''' np |
| + | '''from''' sklearn.datasets '''import''' fetch_openml | ||
| + | '''from''' sklearn.metrics '''import''' confusion_matrix | ||
| + | mnist = fetch_openml('mnist_784', version=1) | ||
| + | X, y = mnist["data"], mnist["target"] | ||
| + | y = y.astype(np.uint8) | ||
| + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | ||
| + | y_train_5 = (y_train == 5) <font color="green"># True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | y_train_perfect_predictions = y_train_5 <font color="green"># притворись, что мы достигли совершенства</font> | ||
| + | print(confusion_matrix(y_train_5, y_train_perfect_predictions)) | ||
| + | <font color="green"># array([[54579, 0], | ||
| + | # [ 0, 5421]])</font> | ||
| − | + | === Аккуратность (англ. Accuracy) === | |
| − | + | Интуитивно понятной, очевидной и почти неиспользуемой метрикой является ''accuracy'' — доля правильных ответов алгоритма: | |
| − | Эта метрика бесполезна в задачах с неравными классами, и это легко показать на примере. | + | : <math> |
| + | accuracy = \dfrac{TP+TN}{TP+TN+FP+FN} | ||
| + | </math> | ||
| + | |||
| + | Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью [[алгоритмы сэмплирования|алгоритмов сэмплирования]] и это легко показать на примере. | ||
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5). | Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5). | ||
Тогда accuracy: | Тогда accuracy: | ||
| − | + | : <math> | |
| + | accuracy = \dfrac{5+90}{5+90+10+5} = 86,4 | ||
| + | </math> | ||
| − | Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую | + | Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую ''аккуратность'': |
| − | + | : <math> | |
| + | accuracy = \dfrac{0+100}{0+100+0+10} = 90,9 | ||
| + | </math> | ||
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов. | При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов. | ||
| − | = | + | <font color="green"># код для для подсчета аккуратности:</font> |
| − | + | <font color="green">'''# Пример классификатора, способного проводить различие между всего лишь двумя | |
| − | + | '''# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST</font> | |
| − | + | '''import''' numpy '''as''' np | |
| − | + | '''from''' sklearn.datasets '''import''' fetch_openml | |
| − | + | '''from''' sklearn.model_selection '''import''' cross_val_predict | |
| − | + | '''from''' sklearn.metrics '''import''' accuracy_score | |
| − | + | '''from''' sklearn.linear_model '''import''' SGDClassifier | |
| − | + | mnist = fetch_openml('mnist_784', version=1) | |
| − | + | X, y = mnist["data"], mnist["target"] | |
| − | + | y = y.astype(np.uint8) | |
| − | + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | |
| − | + | y_train_5 = (y_train == 5)<font color="green"> # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | |
| − | + | y_test_5 = (y_test == 5) | |
| − | + | sgd_clf = SGDClassifier(random_state=42) <font color="green"># классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)</font> | |
| − | + | sgd_clf.fit(X_train, y_train_5) <font color="green"># обучаем классификатор распозновать пятерки на целом обучающем наборе</font> | |
| − | + | y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) | |
| − | + | <font color="green"># print(confusion_matrix(y_train_5, y_train_pred)) | |
| − | + | # array([[53892, 687] | |
| − | + | # [ 1891, 3530]])</font> | |
| − | + | print(accuracy_score(y_train_5, y_train_pred))<font color="green"> # == (53892 + 3530) / (53892 + 3530 + 1891 +687)</font> | |
| − | + | ||
| − | + | <font color="green"># 0.9570333333333333</font> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <font color="green"># | ||
| − | ''' | ||
| − | |||
| − | |||
| − | |||
| − | ''' | ||
| − | |||
| − | |||
| − | ''' | ||
| − | |||
| − | |||
| − | ''' | ||
| − | |||
| − | ''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | ||
| − | |||
| − | == | ||
| − | |||
| − | |||
| − | |||
| − | === | ||
| − | |||
| − | |||
| − | |||
| − | === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [ | ||
| − | |||
| − | |||
| − | |||
| − | === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | === Точность (англ. Precision) === | ||
| − | ''' | + | Точностью (''precision'') называется доля правильных ответов модели в пределах класса {{---}} это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | Precision = \dfrac{TP}{TP+FP} | |
</math> | </math> | ||
| − | |||
| − | + | Именно введение ''precision'' не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня ''False Positive''. | |
| − | |||
| − | |||
| − | + | === Полнота (англ. Recall) === | |
| − | + | Полнота {{---}} это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | Recall = \dfrac{TP}{TP+FN} | |
</math> | </math> | ||
| − | |||
| − | + | Полнота (''recall'') демонстрирует способность алгоритма обнаруживать данный класс вообще. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (''precision'') равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (''recall'') {{---}} отношению диагонального элемента матрицы и суммы всего столбца класса. Формально: | |
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | Precision_c = \dfrac{A_{c,c}}{\sum \limits_{i=1}^{n} A_{c,i}} | |
</math> | </math> | ||
| − | |||
: <math> | : <math> | ||
| − | + | Recall_c = \dfrac{A_{c,c}}{\sum \limits_{i=1}^{n} A_{i,c}} | |
</math> | </math> | ||
| − | === | + | Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется '''macro-averaging'''. |
| − | + | ||
| − | + | <font color="green"># код для для подсчета точности и полноты: | |
| − | </ | + | '''# Пример классификатора, способного проводить различие между всего лишь двумя |
| + | '''# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST</font> | ||
| + | '''import''' numpy '''as''' np | ||
| + | '''from''' sklearn.datasets '''import''' fetch_openml | ||
| + | '''from''' sklearn.model_selection '''import''' cross_val_predict | ||
| + | '''from''' sklearn.metrics '''import''' precision_score, recall_score | ||
| + | '''from''' sklearn.linear_model '''import''' SGDClassifier | ||
| + | mnist = fetch_openml('mnist_784', version=1) | ||
| + | X, y = mnist["data"], mnist["target"] | ||
| + | y = y.astype(np.uint8) | ||
| + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | ||
| + | y_train_5 = (y_train == 5) <font color="green"># True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | sgd_clf = SGDClassifier(random_state=42)<font color="green"> # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)</font> | ||
| + | sgd_clf.fit(X_train, y_train_5) <font color="green"># обучаем классификатор распозновать пятерки на целом обучающем наборе</font> | ||
| + | y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) | ||
| + | <font color="green"># print(confusion_matrix(y_train_5, y_train_pred)) | ||
| + | # array([[53892, 687] | ||
| + | # [ 1891, 3530]])</font> | ||
| + | print(precision_score(y_train_5, y_train_pred)) <font color="green"># == 3530 / (3530 + 687)</font> | ||
| + | print(recall_score(y_train_5, y_train_pred)) <font color="green"># == 3530 / (3530 + 1891)</font> | ||
| + | |||
| + | <font color="green"># 0.8370879772350012 | ||
| + | # 0.6511713705958311</font> | ||
| − | === | + | === F-мера (англ. F-score) === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Precision'' и ''recall'' не зависят, в отличие от ''accuracy'', от соотношения классов и потому применимы в условиях несбалансированных выборок. | |
| + | Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является ''F-мера''. | ||
| − | + | F-мера представляет собой [https://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B5%D0%B4%D0%BD%D0%B5%D0%B5_%D0%B3%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5 гармоническое среднее] между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | : <math> F = \dfrac{ 2 \times precision \times recall }{ precision + recall }</math> | |
| − | + | Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать ''F-меру'' придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма: | |
| − | F- | ||
| − | : | ||
| − | |||
| − | |||
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | F_β = \dfrac{(1+β^2) \times precision \times recall }{ (β^2 \times precision) + recall } | |
</math> | </math> | ||
| − | = | + | где <math>β</math> принимает значения в диапазоне <math>0<β<1</math> если вы хотите отдать приоритет точности, а при <math>β>1</math> приоритет отдается полноте. При <math>β=1</math> формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют <math>F_1</math>). |
| − | |||
| − | |||
| − | |||
| − | + | <div><ul> | |
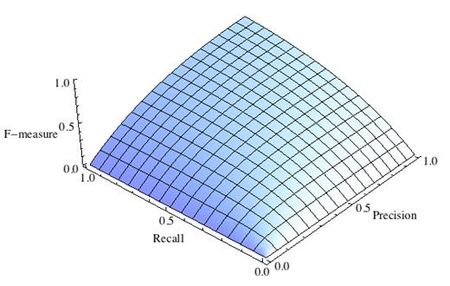
| − | : <math> | + | <li style="display: inline-block;"> [[Файл:F_balanc.jpg|thumb|none|450px|Рис.1 Сбалансированная F-мера, <math>β=1</math>]] </li> |
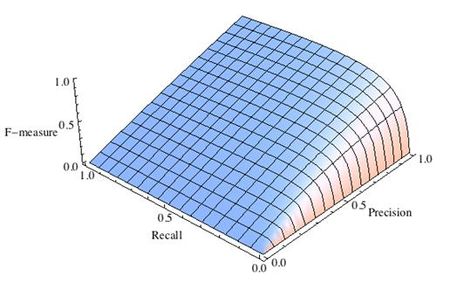
| − | + | <li style="display: inline-block;"> [[Файл:F_prior_Prec.jpg|thumb|none|450px|Рис.2 F-мера c приоритетом точности, <math>β^2=\dfrac{ 1 }{ 4 }</math>]] </li> | |
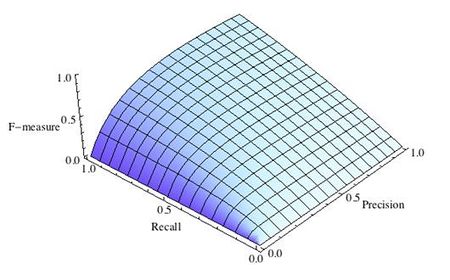
| − | </math> | + | <li style="display: inline-block;"> [[Файл:F_prior_Recal.jpg|thumb|none|450px|Рис.3 F-мера c приоритетом полноты, <math>β^2=2</math>]] </li> |
| + | </ul></div> | ||
| − | + | ''F-мера'' достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю. | |
| − | |||
| − | + | ''F-мера'' является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея "F-меру" гораздо проще ответить на вопрос: "поменялся алгоритм в лучшую сторону или нет?" | |
| − | : | ||
| − | |||
| − | |||
| − | = | + | <font color="green"># код для подсчета метрики F-mera: |
| − | + | '''# Пример классификатора, способного проводить различие между всего лишь двумя | |
| − | + | '''# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST</font> | |
| − | + | '''import''' numpy '''as''' np | |
| − | + | '''from''' sklearn.datasets '''import''' fetch_openml | |
| − | + | '''from''' sklearn.model_selection '''import''' cross_val_predict | |
| − | + | '''from''' sklearn.linear_model '''import''' SGDClassifier | |
| − | + | '''from''' sklearn.metrics '''import''' f1_score | |
| + | mnist = fetch_openml('mnist_784', version=1) | ||
| + | X, y = mnist["data"], mnist["target"] | ||
| + | y = y.astype(np.uint8) | ||
| + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | ||
| + | y_train_5 = (y_train == 5)<font color="green"> # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | sgd_clf = SGDClassifier(random_state=42)<font color="green"> # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)</font> | ||
| + | sgd_clf.fit(X_train, y_train_5) <font color="green"># обучаем классификатор распознавать пятерки на целом обучающем наборе</font> | ||
| + | y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) | ||
| + | print(f1_score(y_train_5, y_train_pred)) | ||
| + | |||
| + | <font color="green"># 0.7325171197343846</font> | ||
| − | === | + | === ROC-кривая === |
| − | |||
| − | + | '''Кривая рабочих характеристик''' (англ. '''Receiver Operating Characteristics curve'''). | |
| − | + | Используется для анализа поведения классификаторов при различных пороговых значениях. | |
| + | Позволяет рассмотреть все пороговые значения для данного классификатора. | ||
| + | Показывает долю ложно положительных примеров (англ. '''false positive rate, FPR''') в сравнении с долей истинно положительных примеров (англ. '''true positive rate, TPR'''). | ||
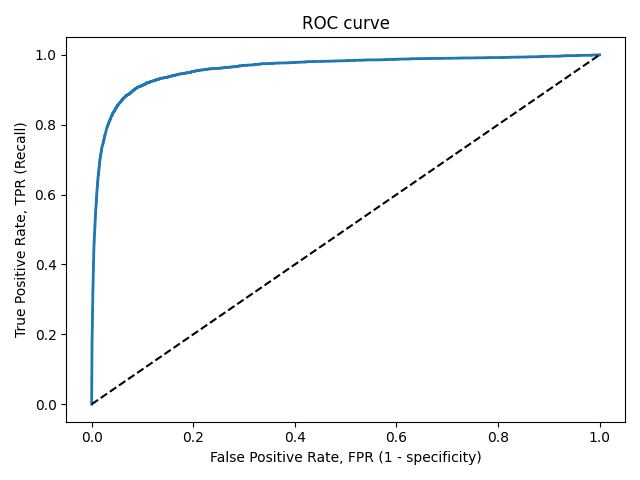
| − | : | + | [[Файл:ROC_2.png]] |
| − | : <math> | + | : <math> TPR = \dfrac{TP}{TP+FN} = Recall</math> |
| − | + | : <math> FPR = \dfrac{FP}{FP+TN} </math> | |
| − | : <math> | ||
| − | + | Доля '''FPR''' {{---}} это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные. | |
| − | + | : <math> FPR = 1 - TNR</math>, | |
| − | + | где '''TNR''' {{---}} доля истинно отрицательных классификаций (англ. '''Тrие Negative Rate'''), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные. | |
| − | |||
| − | + | Доля '''TNR''' также называется '''специфичностью''' (англ. '''specificity'''). Следовательно, ROC-кривая изображает '''чувствительность''' (англ. '''seпsitivity'''), т.е. полноту, в сравнении с разностью '''1 - specificity'''. | |
| − | + | Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это | |
| + | возможно (стремясь к левому верхнему углу). | ||
| − | + | Один из способов сравнения классификаторов предусматривает измерение '''площади под кривой''' (англ. '''Area Under the Curve {{---}} AUC'''). Безупречный классификатор будет иметь площадь под ROC-кривой ('''ROC-AUC'''), равную 1, тогда как чисто случайный классификатор - площадь 0.5. | |
| − | : < | + | <font color="green"># Код отрисовки ROC-кривой |
| + | '''# На примере классификатора, способного проводить различие между всего лишь двумя классами | ||
| + | '''# "пятерка" и "не пятерка" из набора рукописных цифр MNIST</font> | ||
| + | '''from''' sklearn.metrics '''import''' roc_curve | ||
| + | '''import''' matplotlib.pyplot '''as''' plt | ||
| + | '''import''' numpy '''as''' np | ||
| + | '''from''' sklearn.datasets '''import''' fetch_openml | ||
| + | '''from''' sklearn.model_selection '''import''' cross_val_predict | ||
| + | '''from''' sklearn.linear_model '''import''' SGDClassifier | ||
| + | mnist = fetch_openml('mnist_784', version=1) | ||
| + | X, y = mnist["data"], mnist["target"] | ||
| + | y = y.astype(np.uint8) | ||
| + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | ||
| + | y_train_5 = (y_train == 5) <font color="green"># True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | sgd_clf = SGDClassifier(random_state=42) <font color="green"># классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)</font> | ||
| + | sgd_clf.fit(X_train, y_train_5) <font color="green"># обучаем классификатор распозновать пятерки на целом обучающем наборе</font> | ||
| + | y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) | ||
| + | y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") | ||
| + | fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) | ||
| + | def plot_roc_curve(fpr, tpr, label=None): | ||
| + | plt.plot(fpr, tpr, linewidth=2, label=label) | ||
| + | plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal | ||
| + | plt.xlabel('False Positive Rate, FPR (1 - specificity)') | ||
| + | plt.ylabel('True Positive Rate, TPR (Recall)') | ||
| + | plt.title('ROC curve') | ||
| + | plt.savefig("ROC.png") | ||
| + | plot_roc_curve(fpr, tpr) | ||
| + | plt.show() | ||
| − | + | === Precison-recall кривая === | |
| − | + | '''Чувствительность к соотношению классов.''' | |
| + | Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм <math>a(x)</math>, идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма. | ||
| + | Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм <math>b(x)</math>, помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95. | ||
| − | + | '''Precison-recall (PR) кривая.''' Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает '''площадь под PR-кривой''' (англ. '''Area Under the Curve — AUC-PR''') | |
| − | : | + | [[Файл:PR_curve.png]] |
| − | + | <font color="green"># Код отрисовки Precison-recall кривой | |
| + | '''# На примере классификатора, способного проводить различие между всего лишь двумя классами | ||
| + | '''# "пятерка" и "не пятерка" из набора рукописных цифр MNIST</font> | ||
| + | '''from''' sklearn.metrics '''import''' precision_recall_curve | ||
| + | '''import''' matplotlib.pyplot '''as''' plt | ||
| + | '''import''' numpy '''as''' np | ||
| + | '''from''' sklearn.datasets '''import''' fetch_openml | ||
| + | '''from''' sklearn.model_selection '''import''' cross_val_predict | ||
| + | '''from''' sklearn.linear_model '''import''' SGDClassifier | ||
| + | mnist = fetch_openml('mnist_784', version=1) | ||
| + | X, y = mnist["data"], mnist["target"] | ||
| + | y = y.astype(np.uint8) | ||
| + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | ||
| + | y_train_5 = (y_train == 5) <font color="green"># True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | sgd_clf = SGDClassifier(random_state=42)<font color="green"> # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)</font> | ||
| + | sgd_clf.fit(X_train, y_train_5) <font color="green"># обучаем классификатор распозновать пятерки на целом обучающем наборе</font> | ||
| + | y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) | ||
| + | y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") | ||
| + | precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) | ||
| + | def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): | ||
| + | plt.plot(recalls, precisions, linewidth=2) | ||
| + | plt.xlabel('Recall') | ||
| + | plt.ylabel('Precision') | ||
| + | plt.title('Precision-Recall curve') | ||
| + | plt.savefig("Precision_Recall_curve.png") | ||
| + | plot_precision_recall_vs_threshold(precisions, recalls, thresholds) | ||
| + | plt.show() | ||
| − | + | == Оценки качества регрессии == | |
| − | + | Наиболее типичными мерами качества в задачах регрессии являются | |
| − | === | + | === Средняя квадратичная ошибка (англ. Mean Squared Error, MSE) === |
| − | |||
| − | + | ''MSE'' применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | MSE = \dfrac{1}{n}\sum \limits_{i=1}^{n}(a(x_i) - y_i)^2 | |
| − | </math> | + | </math> и |
| − | |||
| − | === | + | === Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE) === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | MAE = \dfrac{1}{n}\sum \limits_{i=1}^{n}|a(x_i) - y_i| | |
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | + | Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации {{---}} <math>R^2</math> | |
| − | === | + | === Коэффициент детерминации === |
| − | |||
: <math> | : <math> | ||
| − | + | R^2 = 1 - \dfrac{\sum \limits_{i=1}^{n}(a(x_i) - y_i)^2}{\sum \limits_{i=1}^{n}(y_i - \overline{y})^2} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | + | Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием. | |
| + | |||
| + | === Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE) === | ||
| − | |||
: <math> | : <math> | ||
| − | + | MAPE = 100\% \times \dfrac{1}{n}\sum \limits_{i=1}^{n} \dfrac{|y_i - a(x_i)|}{|y_i|} | |
</math> | </math> | ||
| − | + | Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений. | |
| − | + | Основная проблема данной ошибки — нестабильность. | |
| − | |||
| − | |||
| − | |||
| − | === | + | === Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE) === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
: <math> | : <math> | ||
| − | + | RMSE = \sqrt{\dfrac{1}{n}\sum \limits_{i=1}^{n}(a(x_i) - y_i)^2} | |
| − | + | </math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. | |
| − | + | === Cимметричная MAPE (англ. Symmetric MAPE, SMAPE) === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | ||
| − | |||
: <math> | : <math> | ||
| − | + | SMAPE = \dfrac{1}{n}\sum \limits_{i=1}^{n} \dfrac{2 \times |y_i - a(x_i)|}{|y_i| + |a(x_i)|} | |
| − | </math> | + | </math> |
| − | + | === Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE) === | |
| − | + | : <math> MASE = \dfrac{\sum \limits_{i=1}^n |Y_i - e_i|}{\frac{n}{n-1}\sum \limits_{i=2}^n | Y_i-Y_{i-1}|} </math> | |
| − | === | ||
| − | |||
| − | : | + | ''MASE'' является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени. |
| − | + | Обратите внимание, что в ''MASE'' мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе - обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами ''MASE'', так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки. | |
| − | |||
| − | + | Недостаток ''MASE'' в том, что её тяжело интерпретировать. Например, ''MASE''=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более. | |
| − | === | + | == Кросс-валидация == |
| − | |||
| − | + | Хороший способ оценки модели предусматривает применение [[Кросс-валидация|кросс-валидации]] (cкользящего контроля или перекрестной проверки). | |
| − | |||
| − | |||
| − | + | В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках. | |
| − | + | == Примечания == | |
| − | + | # [https://www.coursera.org/lecture/vvedenie-mashinnoe-obuchenie/otsienivaniie-kachiestva-xCdqN] Лекция "Оценивание качества" на www.coursera.org | |
| − | + | # [https://stepik.org/lesson/209691/step/8?unit=183195] Лекция на www.stepik.org о кросвалидации | |
| − | + | # [https://stepik.org/lesson/209692/step/5?unit=183196] Лекция на www.stepik.org о метриках качества, Precison и Recall | |
| − | + | # [https://stepik.org/lesson/209692/step/7?unit=183196] Лекция на www.stepik.org о метриках качества, F-мера | |
| − | + | # [https://stepik.org/lesson/209692/step/8?unit=183196] Лекция на www.stepik.org о метриках качества, примеры | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== См. также == | == См. также == | ||
| − | * [[ | + | * [[Оценка качества в задаче кластеризации]] |
| − | * [[ | + | * [[Кросс-валидация]] |
== Источники информации == | == Источники информации == | ||
| − | # [https:// | + | # [https://compscicenter.ru/media/courses/2018-autumn/spb-recommendation/materials/lecture02-linregr_1.pdf] Соколов Е.А. Лекция линейная регрессия |
| − | # [http:// | + | # [http://www.machinelearning.ru/wiki/images/5/59/PZAD2016_04_errors.pdf] - Дьяконов А. Функции ошибки / функционалы качества |
| − | # [ | + | # [https://forecasting.svetunkov.ru/etextbook/forecasting_toolbox/models_quality/] - Оценка качества прогнозных моделей |
| − | # [https:// | + | # [https://shtem.ru/%D0%BE%D1%88%D0%B8%D0%B1%D0%BA%D0%B0-%D0%BF%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0/] - HeinzBr Ошибка прогнозирования: виды, формулы, примеры |
| − | # [https:// | + | # [https://habr.com/ru/company/ods/blog/328372/] - egor_labintcev Метрики в задачах машинного обучения |
| − | + | # [https://habr.com/ru/post/19657/] - grossu Методы оценки качества прогноза | |
| − | + | # [http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%84%D0%B8%D0%BA%D0%B0%D1%86%D0%B8%D1%8F] - К.В.Воронцов, Классификация | |
| + | # [http://www.machinelearning.ru/wiki/index.php?title=CV] - К.В.Воронцов, Скользящий контроль | ||
[[Категория:Машинное обучение]] | [[Категория:Машинное обучение]] | ||
| − | [[Категория: | + | [[Категория:Классификация]] |
| + | [[Категория:Регрессия]] | ||
Текущая версия на 19:06, 4 сентября 2022
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок). Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как "сигнал тревоги", сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как "ложную тревогу".
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как "пропуск цели".
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае "ложной тревоги" потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае "пропуска цели" можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить "пропуск цели", чем "ложную тревогу".
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный - отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок
# Пример классификатора, способного проводить различие между всего лишь двумя
# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
from sklearn.linear_model import SGDClassifier
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD)
sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе
# Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
print(confusion_matrix(y_train_5, y_train_pred))
# array([[53892, 687],
# [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5). Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности:
# Пример классификатора, способного проводить различие между всего лишь двумя
# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import accuracy_score
from sklearn.linear_model import SGDClassifier
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)
sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
# print(confusion_matrix(y_train_5, y_train_pred))
# array([[53892, 687]
# [ 1891, 3530]])
print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687)
# 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты:
# Пример классификатора, способного проводить различие между всего лишь двумя
# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import precision_score, recall_score
from sklearn.linear_model import SGDClassifier
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)
sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
# print(confusion_matrix(y_train_5, y_train_pred))
# array([[53892, 687]
# [ 1891, 3530]])
print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687)
print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891)
# 0.8370879772350012
# 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок. Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея "F-меру" гораздо проще ответить на вопрос: "поменялся алгоритм в лучшую сторону или нет?"
# код для подсчета метрики F-mera:
# Пример классификатора, способного проводить различие между всего лишь двумя
# классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import f1_score
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)
sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
print(f1_score(y_train_5, y_train_pred))
# 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve). Используется для анализа поведения классификаторов при различных пороговых значениях. Позволяет рассмотреть все пороговые значения для данного классификатора. Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 - specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор - площадь 0.5.
# Код отрисовки ROC-кривой
# На примере классификатора, способного проводить различие между всего лишь двумя классами
# "пятерка" и "не пятерка" из набора рукописных цифр MNIST
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.linear_model import SGDClassifier
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)
sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal
plt.xlabel('False Positive Rate, FPR (1 - specificity)')
plt.ylabel('True Positive Rate, TPR (Recall)')
plt.title('ROC curve')
plt.savefig("ROC.png")
plot_roc_curve(fpr, tpr)
plt.show()
Precison-recall кривая
Чувствительность к соотношению классов. Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма. Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
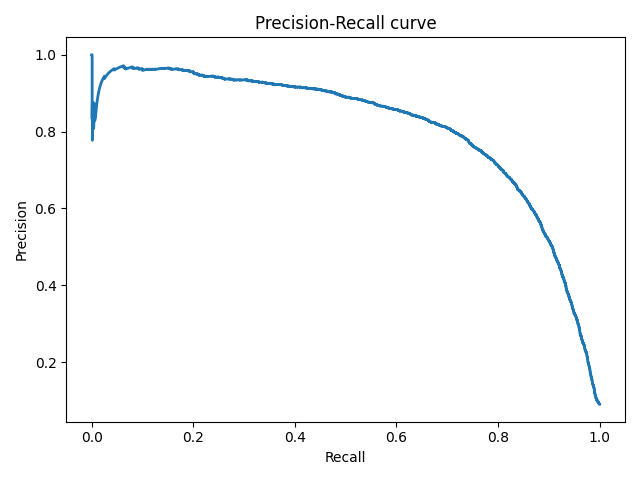
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
# Код отрисовки Precison-recall кривой
# На примере классификатора, способного проводить различие между всего лишь двумя классами
# "пятерка" и "не пятерка" из набора рукописных цифр MNIST
from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.linear_model import SGDClassifier
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)
sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(recalls, precisions, linewidth=2)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall curve')
plt.savefig("Precision_Recall_curve.png")
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений. Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени. Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе - обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция "Оценивание качества" на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] - Дьяконов А. Функции ошибки / функционалы качества
- [8] - Оценка качества прогнозных моделей
- [9] - HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] - egor_labintcev Метрики в задачах машинного обучения
- [11] - grossu Методы оценки качества прогноза
- [12] - К.В.Воронцов, Классификация
- [13] - К.В.Воронцов, Скользящий контроль