Префикс-функция — различия между версиями
Vasin (обсуждение | вклад) (→Оптимизация) |
Vasin (обсуждение | вклад) (→Оптимизация) |
||
| Строка 39: | Строка 39: | ||
Вносятся несколько важных замечаний: | Вносятся несколько важных замечаний: | ||
*Следует заметить, что <tex>\pi(i) \le \pi(i-1) + 1</tex>. По определению префикс функции верно, что <tex>s[1..\pi(i)] = s[i - \pi(i)..i]</tex>. Отсюда получается, что <tex>s[1..\pi(i - 1)] = s[i - \pi(i)..i - 1]</tex>. Поскольку <tex>\pi</tex> это наибольший префикс равный суффиксу, то <tex>\pi(i - 1) >= \pi(i) - 1</tex>. | *Следует заметить, что <tex>\pi(i) \le \pi(i-1) + 1</tex>. По определению префикс функции верно, что <tex>s[1..\pi(i)] = s[i - \pi(i)..i]</tex>. Отсюда получается, что <tex>s[1..\pi(i - 1)] = s[i - \pi(i)..i - 1]</tex>. Поскольку <tex>\pi</tex> это наибольший префикс равный суффиксу, то <tex>\pi(i - 1) >= \pi(i) - 1</tex>. | ||
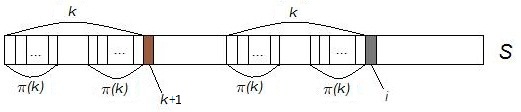
| − | *Избавимся от явных сравнений строк. Для этого подберем такое <tex>k</tex>, что <tex>k = \pi(i) - 1</tex>. | + | *Избавимся от явных сравнений строк. Для этого подберем такое <tex>k</tex>, что <tex>k = \pi(i) - 1</tex>. Делать это нужно следующим образом. За исходное <tex>k</tex> нужно взять <tex>\pi(i - 1)</tex>, что следует из первого пункта. В случае, когда символы <tex>s[k+1]</tex> и <tex>s[i]</tex> не совпадают, <tex>\pi(k)</tex> {{---}} следующая длина потенциального наибольшего общего префикса, что видно из рисунка. Последнее утверждение верно, пока <tex>k>0</tex>, что позволит всегда найти его следующее значение. Если <tex>k=0</tex>, то <tex>\pi(i)=1</tex> при <tex>s[i] = s[1]</tex> , иначе <tex>\pi(i)=0</tex>. |
| − | |||
[[Файл:Prefix2.jpg]] | [[Файл:Prefix2.jpg]] | ||
Версия 16:36, 12 июня 2012
Префикс-функция строки — функция , где принадлежит расширенному множеству натуральных чисел.
Содержание
Алгоритм
Наивный алгоритм вычисляет префикс функцию непосредственно по определению, сравнивая префиксы и суффиксы строк.
Псевдокод
Prefix_function () = [0,..0] for i = 1 to n for k = 1 to i - 1 if s[1..k] == s[i - k + 1..i] [i] = k return
Пример
Рассмотрим строку abcabcd, для которой значение префикс-функции равно .
| Шаг | Строка | Значение функции |
|---|---|---|
| a | 0 | |
| ab | 0 | |
| abc | 0 | |
| abca | 1 | |
| abcab | 2 | |
| abcabc | 3 | |
| abcabcd | 0 |
Время работы
Всего итераций цикла, на каждой из который происходит сравнение строк за , что дает в итоге .
Оптимизация
Вносятся несколько важных замечаний:
- Следует заметить, что . По определению префикс функции верно, что . Отсюда получается, что . Поскольку это наибольший префикс равный суффиксу, то .
- Избавимся от явных сравнений строк. Для этого подберем такое , что . Делать это нужно следующим образом. За исходное нужно взять , что следует из первого пункта. В случае, когда символы и не совпадают, — следующая длина потенциального наибольшего общего префикса, что видно из рисунка. Последнее утверждение верно, пока , что позволит всегда найти его следующее значение. Если , то при , иначе .
Псевдокод
Prefix_function () [1] = 0 k = 0 for i = 2 to n while k > 0 && s[i] != s[k + 1] k = [k] if s[i] == s[k + 1] k++ [i] = k return
Время работы
Время работы алгоритма составит . Для доказательства этого нужно заметить, что итоговое количество итераций цикла составит время работы алгоритма. Теперь стоит отметить, что увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение . Внутри цикла значение лишь уменьшается, а из предыдущего утверждения получается, что оно не может суммарно уменьшиться больше, чем раз, значит цикл в итоге выполнится менее раз, что дает итоговую оценку времени алгоритма .
Литература
Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296.