Рекомендательные системы — различия между версиями
Ponomarev (обсуждение | вклад) м (→Холодный старт) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 119 промежуточных версий 7 участников) | |||
| Строка 3: | Строка 3: | ||
== Обзор и постановка задачи == | == Обзор и постановка задачи == | ||
| − | Основная задача рекомендательных систем {{---}} проинформировать пользователя о товарах или услугах, которые будут для него наиболее интересными и актуальными. Разнообразие таких систем можно проиллюстрировать основными характеристиками: | + | Основная задача рекомендательных систем<ref>[https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%BA%D0%BE%D0%BC%D0%B5%D0%BD%D0%B4%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0 Рекомендательные системы]</ref> {{---}} проинформировать пользователя о товарах или услугах, которые будут для него наиболее интересными и актуальными. Разнообразие таких систем можно проиллюстрировать основными характеристиками: |
* предмет рекомендации; | * предмет рекомендации; | ||
| Строка 13: | Строка 13: | ||
* прозрачность рекомендации. | * прозрачность рекомендации. | ||
| − | В центре таких систем лежит матрица предпочтений. В этой матрице одна из осей отвечает за пользователей, вторая за объекты рекомендации. Заполнена же эта матрица значениями по заданной шкале (например от <tex>1</tex> до <tex>5</tex>). | + | В центре таких систем лежит матрица предпочтений. В этой матрице одна из осей отвечает за пользователей, вторая за объекты рекомендации. Заполнена же эта матрица значениями по заданной шкале (например от <tex>1</tex> до <tex>5</tex>). Так как каждый пользователь обычно может оценить только небольшую часть объектов, то данная матрица очень разрежена. Задача системы {{---}} обобщение информации и предсказание отношения пользователя к объекту (заполнение пропущенных значений матрицы). |
| − | + | Данные, сообщающие предпочтения пользователя, можно получить двумя способами: | |
| − | * явно (англ. ''explicit ratings''); | + | * явно (англ. ''explicit feedback'', ''explicit ratings''); |
| − | * неявно (англ. ''implicit ratings''). | + | * неявно (англ. ''implicit feedback'', ''implicit ratings''). |
| − | + | При явном оценивании пользователь сам показывает, насколько ему интересен тот или иной объект. Типичным примером данных, полученных при явном оценивании, являются рейтинги, проставленные пользователями объектам. На практике таких данных обычно мало. | |
| + | Гораздо больше имеется информации о неявных предпочтениях пользователя: просмотры, клики, добавления в закладки. Однако по таким данным не всегда можно сделать явный вывод об отношении пользователя к объекту. Например, если пользователь посмотрел фильм, то это означает, что до просмотра он ему был интересен, но сделать вывод о том, понравился ли ему фильм, нельзя. | ||
| + | В большинстве рекомендательных систем эти два подхода используются вместе, тем самым минимизируются недостатки каждого из них в отдельности. | ||
| − | Формализуем задачу. Имеется множество пользователей <tex> u \in U </tex>, множество объектов <tex> i \in I </tex> и множество событий <tex> (r_{ui}, u, i,\dots) \in D </tex> (действия, которые совершают пользователи с объектами). Каждое событие задается пользователем <tex> u </tex>, объектом <tex> i </tex>, своим результатом <tex> r_{ui} </tex> и, возможно, но не обязательно, другими характеристиками. По итогу требуется: | + | Формализуем задачу. Имеется множество пользователей <tex> u \in U </tex>, множество объектов <tex> i \in I </tex> и множество событий <tex> (r_{ui}, u, i,\dots) \in D </tex> (действия, которые совершают пользователи с объектами). Каждое событие задается пользователем <tex> u </tex>, объектом <tex> i </tex>, своим результатом <tex> r_{ui} </tex> и, возможно, но не обязательно, другими характеристиками. По итогу от рекомендательной системы требуется: |
| − | * | + | * предсказывать предпочтение пользователя <tex> u </tex> к объекту <tex> i </tex>: <tex> \hat{r}_{ui} = Predict(u, i,\dots) \approx r_{ui}; </tex> |
| − | * персональные рекомендации: <tex> u | + | * выдавать персональные рекомендации для пользователя <tex> u </tex>: <tex> Recommend_k(u,\dots) = (i_1,\dots, i_k); </tex> |
| − | * похожие | + | * определять объекты, похожие на объект <tex>i</tex>: <tex>Similar_M(i) = (i_1,\dots, i_M). </tex> |
==Кластеризация пользователей== | ==Кластеризация пользователей== | ||
| Строка 44: | Строка 46: | ||
Проблемы алгоритма: | Проблемы алгоритма: | ||
| − | * | + | * нечего рекомендовать новым пользователям, так как их невозможно отнести к какому-либо кластеру; |
| − | * | + | * не учитывается контекст и специфика пользователя; |
| − | * | + | * если в кластере нет оценки объекта, то предсказание невозможно. |
== Холодный старт == | == Холодный старт == | ||
| Строка 53: | Строка 55: | ||
'''Холодный старт''' (англ. ''cold start'') {{---}} ситуация, когда ещё не накоплено достаточное количество данных для корректной работы рекомендательной системы. | '''Холодный старт''' (англ. ''cold start'') {{---}} ситуация, когда ещё не накоплено достаточное количество данных для корректной работы рекомендательной системы. | ||
}} | }} | ||
| − | Данная проблема актуальна для новых объектов или объектов, | + | Данная проблема актуальна для новых объектов или объектов, с которыми пользователи редко совершают действия. Если средний рейтинг посчитан по оценкам всего трёх пользователей, такая оценка явно не будет достоверной, и пользователи это понимают. Часто в таких ситуациях рейтинги искусственно корректируют. |
| − | Первый способ | + | '''Первый способ.''' Предлагается показывать не среднее значение, а сглаженное среднее (англ. ''damped mean''). Смысл таков: при малом количестве оценок отображаемый рейтинг больше тяготеет к некому безопасному «среднему» показателю, а как только набирается достаточное количество новых оценок, «усредняющая» корректировка перестает действовать. |
| − | + | '''Второй способ.''' Для объекта считается средний рейтинг, затем определяется доверительный интервал(англ. ''сonfidence interval'') этого рейтинга. Математически, чем больше оценок, тем меньше вариация среднего и, значит, больше уверенность в его корректности. А в качестве рейтинга объекта можно выводить, например, нижнюю границу интервала (англ. ''low CI bound''). При этом понятно, что такая система будет достаточно консервативной, с тенденцией к занижению оценок по новым объектам. | |
== User-based и item-based алгоритмы == | == User-based и item-based алгоритмы == | ||
| − | Заменим жесткую кластеризацию на предположение, что | + | === User-based алгоритм === |
| + | Заменим жесткую кластеризацию на предположение, что объект понравится пользователю, если он понравился похожим пользователям. Тогда предпочтение пользователя <tex>u</tex> к объекту <tex>i</tex> можно записать следующим образом: | ||
| − | <tex> \hat{r}_{ui} = \bar{r}_u + \dfrac{\sum_{v \in U_i}{}{sim(u, v)(r_{vi} - \bar{r}_v)}}{\sum_{v \in {U_i}}{}{sim(u, v)}} </tex> | + | <tex> \hat{r}_{ui} = \bar{r}_u + \dfrac{\sum_{v \in U_i}{}{sim(u, v)(r_{vi} - \bar{r}_v)}}{\sum_{v \in {U_i}}{}{sim(u, v)}} </tex>, где <tex>\bar{r}_u</tex> {{---}} средняя оценка, проставленная пользователем <tex> u </tex>, а <tex> sim(u,v) </tex> {{---}} мера схожести пользователей <tex>u</tex> и <tex>v</tex>. |
Однако у этого алгоритма есть недостатки: | Однако у этого алгоритма есть недостатки: | ||
| − | * | + | * холодный старт — новые объекты никому не рекомендуются; |
| − | * | + | * нечего рекомендовать новым/нетипичным пользователям. |
| − | + | === Item-based алгоритм === | |
| + | Также имеется абсолютно симметричный алгоритм. Теперь будем считать, что объект понравится пользователю, если ему понравились похожие объекты. Предпочтение пользователя <tex>u</tex> к объекту <tex>i</tex> запишется так: | ||
| − | <tex> \hat{r}_{ui} = \bar{r}_i + \dfrac{\sum_{j \in I_u}{}{sim(i, j)(r_{uj} - \bar{r}_j)}}{\sum_{j \in {I_u}}{}{sim(i, j)}} </tex> | + | <tex> \hat{r}_{ui} = \bar{r}_i + \dfrac{\sum_{j \in I_u}{}{sim(i, j)(r_{uj} - \bar{r}_j)}}{\sum_{j \in {I_u}}{}{sim(i, j)}} </tex>, где <tex>\bar{r}_i</tex> {{---}} средняя оценка, проставленная объекту <tex> i </tex>, а <tex> sim(i, j) </tex> {{---}} мера схожести объектов <tex>i</tex> и <tex>j</tex>. |
У такого подхода остается недостаток в виде холодного старта и при этом рекомендации становятся тривиальными. | У такого подхода остается недостаток в виде холодного старта и при этом рекомендации становятся тривиальными. | ||
| − | + | Cтоит отметить, что ресурсоемкость вычислений такими методами высока: для предсказаний необходимо держать в памяти все оценки всех пользователей. | |
==Алгоритм SVD== | ==Алгоритм SVD== | ||
| − | + | Попробуем воспользоваться [[Сингулярное разложение | сингулярным разложением (SVD)]] для задачи рекомендации. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Разложим матрицу оценок <tex> R </tex> с использованием сингулярного разложения: | |
| + | <tex> R_{n \times m} = U_{n \times n} \times \Sigma_{n \times m} \times V^T_{m \times m} </tex>. | ||
| + | Применяя усеченное разложение, получим следующее: | ||
| + | <tex> R'_{n \times m} = U'_{n \times d} \times \Sigma '_{d \times d} \times V'^T_{d \times m} </tex>. | ||
| + | Из свойств сингулярного разложения мы знаем, что матрица <tex> R'_{n \times m} </tex> является наилучшим низкоранговым приближением с точки зрения средне-квадратичного отклонения. Несколько упростим запись выражения: запишем произведение первых двух матриц <tex> \tilde{U}_{n \times d} = U'_{n \times d} \times \Sigma '_{d \times d} </tex>, а матрицу <tex> V'^T_{d \times m} </tex> обозначим как <tex> \tilde{V}_{d \times m} </tex>. Получим формулу <tex> R'_{n \times m} = \tilde{U}_{n \times d} \times \tilde{V}_{d \times m} </tex>. Интерпретировать полученную формулу стоит следующим образом: приближенная матрица оценок может быть вычислена как произведение усеченных матриц пользователей и оценок. | ||
| − | + | Благодаря использованию такого усечения можно решить одну из главных проблем всех ранее упомянутых алгоритмов: ресурсоемкость вычислений. | |
| − | + | [[Файл:RecommendSVD.png|450px|thumb|right|SVD для рекомендательных систем.]] | |
| − | Чтобы предсказать оценку пользователя <tex> | + | Чтобы предсказать оценку пользователя <tex> u </tex> для объекта <tex> i </tex>, берём некоторый вектор <tex> p_u </tex> для данного пользователя и вектор данного объекта <tex> q_i </tex>. Получаем необходимое предсказание: <tex> \hat{r}_{ui} = \langle p_u,q_i \rangle </tex>. |
Помимо предсказания оценок, алгоритм позволяет выявлять скрытые признаки объектов и интересы пользователей. | Помимо предсказания оценок, алгоритм позволяет выявлять скрытые признаки объектов и интересы пользователей. | ||
| + | Например, может так получиться, что на первой координате вектора у каждого пользователя будет стоять число, показывающее, похож ли пользователь больше на мальчика или на девочку, на второй координате — число, отражающее примерный возраст пользователя. У фильма же первая координата будет показывать, интересен ли он больше мальчикам или девочкам, а вторая — какой возрастной группе пользователей он интересен. | ||
| − | Однако | + | Однако данный алгоритм имеет ряд проблем: |
| − | + | * матрица оценок <tex> R </tex> полностью не известна, поэтому просто взять SVD разложение не представляется возможным; | |
| − | *<tex> R </tex> | + | * Сингулярное разложение не единственное, поэтому даже если какое-то разложение будет найдено, нет гарантии, что первая координата в нем будет соответствовать некоторым выбранным характеристикам пользователя. |
| − | * | ||
==Решение проблемы матрицы оценок== | ==Решение проблемы матрицы оценок== | ||
| − | |||
| − | |||
| − | <tex> | + | Для решения проблем, связанных с матрицей оценок <tex>R</tex>, построим модель. |
| − | <tex> \Theta = {p_u, q_i \mid u \in U, i \in I} </tex> | + | Модель будет зависеть от следующих параметров: вектор пользователей и вектор объектов. Для заданных параметров <tex> u </tex> и <tex>i</tex> возьмем вектор пользователя <tex> p_u </tex> и вектор объекта <tex>q_i</tex>, затем для предсказания оценки получим их скалярное произведение, как и в алгоритме SVD: |
| + | <tex> \hat{r}_{ui}(\Theta) = p^T_uq_i </tex>, где <tex> \Theta = \{p_u, q_i \mid u \in U, i \in I\} </tex>. | ||
Но вектора пока не известны, их нужно получить. Имеются оценки пользователей, при помощи которых можно найти оптимальные параметры, при которых модель предскажет оценки наилучшим образом: | Но вектора пока не известны, их нужно получить. Имеются оценки пользователей, при помощи которых можно найти оптимальные параметры, при которых модель предскажет оценки наилучшим образом: | ||
| − | |||
<tex> E_{(u,i)}(\hat{r}_{ui}(\Theta) - r_{ui})^2 \to min_{\Theta} </tex>. | <tex> E_{(u,i)}(\hat{r}_{ui}(\Theta) - r_{ui})^2 \to min_{\Theta} </tex>. | ||
| − | То есть, нужно найти такие параметры <tex> \Theta </tex>, чтобы квадрат ошибки был наименьшим. Однако ситуация следующая: оптимизация приведет к наименьшим ошибкам в будущем, но как именно оценки будут спрашивать {{---}} неизвестно. Следовательно, это нельзя оптимизировать. Однако, так как оценки, уже проставленные пользователями, известны, постараемся минимизировать ошибку на тех данных, что у нас уже есть. Также | + | То есть, нужно найти такие параметры <tex> \Theta </tex>, чтобы квадрат ошибки был наименьшим. Однако ситуация следующая: оптимизация приведет к наименьшим ошибкам в будущем, но как именно оценки будут спрашивать {{---}} неизвестно. Следовательно, это нельзя оптимизировать. Однако, так как оценки, уже проставленные пользователями, известны, постараемся минимизировать ошибку на тех данных, что у нас уже есть. Также воспользуемся [[Регуляризация | регуляризацией]]. В качестве регуляризатора будет выступать слагаемое <tex>\lambda \sum_{\theta \in \Theta}{\theta^2}</tex>. Получим следующее: |
| − | <tex> \sum_{(u,i) \in D}{(\hat{r}_{ui}(\Theta) - r_{ui})^2} + \lambda \sum_{\theta \in \Theta}{\theta^2} \to min_{\Theta} </tex> | + | <tex> \sum_{(u,i) \in D}{(\hat{r}_{ui}(\Theta) - r_{ui})^2} + \lambda \sum_{\theta \in \Theta}{\theta^2} \to min_{\Theta} </tex>. |
| − | |||
| − | |||
==Численная оптимизация== | ==Численная оптимизация== | ||
| − | |||
| − | + | Чтобы найти оптимальные параметры построенной модели необходимо оптимизировать следующий функционал: | |
| − | + | <tex> J(\Theta) = \sum_{(u,i) \in D}{(p^T_uq_i - r_{ui})^2} + \lambda (\sum_u{||p_u||^2} + \sum_i{||q_i||^2}) </tex>. | |
| − | + | Множество параметров: для каждого объекта и пользователя есть свой вектор, который нужно оптимизировать. Чтобы найти минимум функции можно использовать [[ Стохастический градиентный спуск | метод градиентного спуска]]. Для этого нам понадобится градиент {{---}} вектор из частных производных по каждому параметру, который в нашем случае будет выглядеть так: | |
| − | + | <tex> \nabla J(\Theta) = (\dfrac{\partial J}{\partial \theta_1}, \dfrac{\partial J}{\partial \theta_2},\dots,\dfrac{\partial J}{\partial \theta_n})^T </tex>. | |
| − | <tex> \Theta_{t+1} = \Theta_t - \eta \nabla J(\Theta) </tex> | + | Шаг градиентного спуска можно записать следующим образом: <tex> \Theta_{t+1} = \Theta_t - \eta \nabla J(\Theta) </tex>, где <tex> \eta </tex> {{---}} коэффициент скорости обучения. |
| − | |||
| − | |||
==Измерение качества рекомендаций== | ==Измерение качества рекомендаций== | ||
| − | + | Зачастую качество рекомендаций измеряется с помощью функции ошибки [[ Оценка_качества_в_задачах_классификации_и_регрессии#.D0.9A.D0.BE.D1.80.D0.B5.D0.BD.D1.8C_.D0.B8.D0.B7_.D1.81.D1.80.D0.B5.D0.B4.D0.BD.D0.B5.D0.B9_.D0.BA.D0.B2.D0.B0.D0.B4.D1.80.D0.B0.D1.82.D0.B8.D1.87.D0.BD.D0.BE.D0.B9_.D0.BE.D1.88.D0.B8.D0.B1.D0.BA.D0.B8_.28.D0.B0.D0.BD.D0.B3.D0.BB._Root_Mean_Squared_Error.2C_RMSE.29 | RMSE]]: | |
| − | <tex> RMSE = \sqrt{\dfrac{1}{|D|} \sum_{(u,i) \in D}{(\hat{r}_{ui} - r_{ui})^2}} </tex> | + | <tex> RMSE = \sqrt{\dfrac{1}{|D|} \sum_{(u,i) \in D}{(\hat{r}_{ui} - r_{ui})^2}} </tex>. |
| − | + | Данный способ, хоть и является стандартным для измерением качества, имеет ряд недостатков: | |
| − | + | * пользователи с большим разбросом оценок будут влиять на значение метрики больше, чем остальные; | |
| − | * | + | * ошибка в предсказании высокой оценки имеет такой же вес, что и ошибка в предсказании низкой оценки; |
| − | * | + | * есть риск плохого ранжирования при почти идеальной RMSE и наоборот. |
| − | * | ||
Существуют при этом и другие метрики {{---}} метрики ранжирования, на основе полноты и точности. Однако они не так популярны и используются значительно реже. | Существуют при этом и другие метрики {{---}} метрики ранжирования, на основе полноты и точности. Однако они не так популярны и используются значительно реже. | ||
==См. также== | ==См. также== | ||
| + | * [[Кластеризация]] | ||
* [[Регуляризация]] | * [[Регуляризация]] | ||
| − | * [[ | + | * [[Оценка качества в задаче кластеризации]] |
| − | * [[ | + | * [[Оценка качества в задачах классификации и регрессии]] |
| − | + | == Примечания == | |
| + | <references/> | ||
== Источники информации== | == Источники информации== | ||
* [https://habr.com/ru/company/yandex/blog/241455/ Как работают рекомендательные системы.] | * [https://habr.com/ru/company/yandex/blog/241455/ Как работают рекомендательные системы.] | ||
| Строка 166: | Строка 156: | ||
* [https://neurohive.io/ru/osnovy-data-science/rekomendatelnye-sistemy-modeli-i-ocenka/ Анатомия рекомендательных систем.] | * [https://neurohive.io/ru/osnovy-data-science/rekomendatelnye-sistemy-modeli-i-ocenka/ Анатомия рекомендательных систем.] | ||
* [http://www.mathnet.ru/links/4d5ff6f460c0d9409ce16b558725408d/ista26.pdf Рекомендательные системы: обзор основных постановок и результатов.] | * [http://www.mathnet.ru/links/4d5ff6f460c0d9409ce16b558725408d/ista26.pdf Рекомендательные системы: обзор основных постановок и результатов.] | ||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Рекомендательные системы]] | ||
Текущая версия на 19:27, 4 сентября 2022
Рекомендательные системы — программы, которые пытаются предсказать, какие объекты будут интересны пользователю, имея определенную информацию о его профиле.
Содержание
Обзор и постановка задачи
Основная задача рекомендательных систем[1] — проинформировать пользователя о товарах или услугах, которые будут для него наиболее интересными и актуальными. Разнообразие таких систем можно проиллюстрировать основными характеристиками:
- предмет рекомендации;
- цель рекомендации;
- контекст рекомендации;
- источник рекомендации;
- степень персонализации;
- формат рекомендации;
- прозрачность рекомендации.
В центре таких систем лежит матрица предпочтений. В этой матрице одна из осей отвечает за пользователей, вторая за объекты рекомендации. Заполнена же эта матрица значениями по заданной шкале (например от до ). Так как каждый пользователь обычно может оценить только небольшую часть объектов, то данная матрица очень разрежена. Задача системы — обобщение информации и предсказание отношения пользователя к объекту (заполнение пропущенных значений матрицы).
Данные, сообщающие предпочтения пользователя, можно получить двумя способами:
- явно (англ. explicit feedback, explicit ratings);
- неявно (англ. implicit feedback, implicit ratings).
При явном оценивании пользователь сам показывает, насколько ему интересен тот или иной объект. Типичным примером данных, полученных при явном оценивании, являются рейтинги, проставленные пользователями объектам. На практике таких данных обычно мало. Гораздо больше имеется информации о неявных предпочтениях пользователя: просмотры, клики, добавления в закладки. Однако по таким данным не всегда можно сделать явный вывод об отношении пользователя к объекту. Например, если пользователь посмотрел фильм, то это означает, что до просмотра он ему был интересен, но сделать вывод о том, понравился ли ему фильм, нельзя. В большинстве рекомендательных систем эти два подхода используются вместе, тем самым минимизируются недостатки каждого из них в отдельности.
Формализуем задачу. Имеется множество пользователей , множество объектов и множество событий (действия, которые совершают пользователи с объектами). Каждое событие задается пользователем , объектом , своим результатом и, возможно, но не обязательно, другими характеристиками. По итогу от рекомендательной системы требуется:
- предсказывать предпочтение пользователя к объекту :
- выдавать персональные рекомендации для пользователя :
- определять объекты, похожие на объект :
Кластеризация пользователей
| Определение: |
| Коллаборативная фильтрация (англ. collaborative filtering) — один из методов построения прогнозов (рекомендаций) в рекомендательных системах, использующий известные предпочтения (оценки) группы пользователей для прогнозирования неизвестных предпочтений другого пользователя. |
Основная идея метода — похожим пользователям нравятся похожие объекты.
Алгоритм можно разбить на следующие шаги:
- Выбор условной меры схожести пользователей по истории их оценок .
- Объединение пользователей в группы (кластеры) так, чтобы похожие пользователи оказывались в одном кластере .
- Предсказание оценки пользователя: средняя оценка кластера этому объекту .
Проблемы алгоритма:
- нечего рекомендовать новым пользователям, так как их невозможно отнести к какому-либо кластеру;
- не учитывается контекст и специфика пользователя;
- если в кластере нет оценки объекта, то предсказание невозможно.
Холодный старт
| Определение: |
| Холодный старт (англ. cold start) — ситуация, когда ещё не накоплено достаточное количество данных для корректной работы рекомендательной системы. |
Данная проблема актуальна для новых объектов или объектов, с которыми пользователи редко совершают действия. Если средний рейтинг посчитан по оценкам всего трёх пользователей, такая оценка явно не будет достоверной, и пользователи это понимают. Часто в таких ситуациях рейтинги искусственно корректируют.
Первый способ. Предлагается показывать не среднее значение, а сглаженное среднее (англ. damped mean). Смысл таков: при малом количестве оценок отображаемый рейтинг больше тяготеет к некому безопасному «среднему» показателю, а как только набирается достаточное количество новых оценок, «усредняющая» корректировка перестает действовать.
Второй способ. Для объекта считается средний рейтинг, затем определяется доверительный интервал(англ. сonfidence interval) этого рейтинга. Математически, чем больше оценок, тем меньше вариация среднего и, значит, больше уверенность в его корректности. А в качестве рейтинга объекта можно выводить, например, нижнюю границу интервала (англ. low CI bound). При этом понятно, что такая система будет достаточно консервативной, с тенденцией к занижению оценок по новым объектам.
User-based и item-based алгоритмы
User-based алгоритм
Заменим жесткую кластеризацию на предположение, что объект понравится пользователю, если он понравился похожим пользователям. Тогда предпочтение пользователя к объекту можно записать следующим образом:
, где — средняя оценка, проставленная пользователем , а — мера схожести пользователей и .
Однако у этого алгоритма есть недостатки:
- холодный старт — новые объекты никому не рекомендуются;
- нечего рекомендовать новым/нетипичным пользователям.
Item-based алгоритм
Также имеется абсолютно симметричный алгоритм. Теперь будем считать, что объект понравится пользователю, если ему понравились похожие объекты. Предпочтение пользователя к объекту запишется так:
, где — средняя оценка, проставленная объекту , а — мера схожести объектов и .
У такого подхода остается недостаток в виде холодного старта и при этом рекомендации становятся тривиальными.
Cтоит отметить, что ресурсоемкость вычислений такими методами высока: для предсказаний необходимо держать в памяти все оценки всех пользователей.
Алгоритм SVD
Попробуем воспользоваться сингулярным разложением (SVD) для задачи рекомендации.
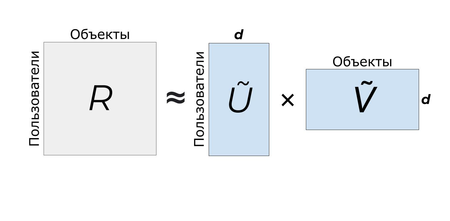
Разложим матрицу оценок с использованием сингулярного разложения: . Применяя усеченное разложение, получим следующее: . Из свойств сингулярного разложения мы знаем, что матрица является наилучшим низкоранговым приближением с точки зрения средне-квадратичного отклонения. Несколько упростим запись выражения: запишем произведение первых двух матриц , а матрицу обозначим как . Получим формулу . Интерпретировать полученную формулу стоит следующим образом: приближенная матрица оценок может быть вычислена как произведение усеченных матриц пользователей и оценок.
Благодаря использованию такого усечения можно решить одну из главных проблем всех ранее упомянутых алгоритмов: ресурсоемкость вычислений.
Чтобы предсказать оценку пользователя для объекта , берём некоторый вектор для данного пользователя и вектор данного объекта . Получаем необходимое предсказание: .
Помимо предсказания оценок, алгоритм позволяет выявлять скрытые признаки объектов и интересы пользователей. Например, может так получиться, что на первой координате вектора у каждого пользователя будет стоять число, показывающее, похож ли пользователь больше на мальчика или на девочку, на второй координате — число, отражающее примерный возраст пользователя. У фильма же первая координата будет показывать, интересен ли он больше мальчикам или девочкам, а вторая — какой возрастной группе пользователей он интересен.
Однако данный алгоритм имеет ряд проблем:
- матрица оценок полностью не известна, поэтому просто взять SVD разложение не представляется возможным;
- Сингулярное разложение не единственное, поэтому даже если какое-то разложение будет найдено, нет гарантии, что первая координата в нем будет соответствовать некоторым выбранным характеристикам пользователя.
Решение проблемы матрицы оценок
Для решения проблем, связанных с матрицей оценок , построим модель.
Модель будет зависеть от следующих параметров: вектор пользователей и вектор объектов. Для заданных параметров и возьмем вектор пользователя и вектор объекта , затем для предсказания оценки получим их скалярное произведение, как и в алгоритме SVD: , где .
Но вектора пока не известны, их нужно получить. Имеются оценки пользователей, при помощи которых можно найти оптимальные параметры, при которых модель предскажет оценки наилучшим образом: .
То есть, нужно найти такие параметры , чтобы квадрат ошибки был наименьшим. Однако ситуация следующая: оптимизация приведет к наименьшим ошибкам в будущем, но как именно оценки будут спрашивать — неизвестно. Следовательно, это нельзя оптимизировать. Однако, так как оценки, уже проставленные пользователями, известны, постараемся минимизировать ошибку на тех данных, что у нас уже есть. Также воспользуемся регуляризацией. В качестве регуляризатора будет выступать слагаемое . Получим следующее: .
Численная оптимизация
Чтобы найти оптимальные параметры построенной модели необходимо оптимизировать следующий функционал:
.
Множество параметров: для каждого объекта и пользователя есть свой вектор, который нужно оптимизировать. Чтобы найти минимум функции можно использовать метод градиентного спуска. Для этого нам понадобится градиент — вектор из частных производных по каждому параметру, который в нашем случае будет выглядеть так:
.
Шаг градиентного спуска можно записать следующим образом: , где — коэффициент скорости обучения.
Измерение качества рекомендаций
Зачастую качество рекомендаций измеряется с помощью функции ошибки RMSE:
.
Данный способ, хоть и является стандартным для измерением качества, имеет ряд недостатков:
- пользователи с большим разбросом оценок будут влиять на значение метрики больше, чем остальные;
- ошибка в предсказании высокой оценки имеет такой же вес, что и ошибка в предсказании низкой оценки;
- есть риск плохого ранжирования при почти идеальной RMSE и наоборот.
Существуют при этом и другие метрики — метрики ранжирования, на основе полноты и точности. Однако они не так популярны и используются значительно реже.
См. также
- Кластеризация
- Регуляризация
- Оценка качества в задаче кластеризации
- Оценка качества в задачах классификации и регрессии