Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах — различия между версиями
| Строка 2: | Строка 2: | ||
===Минимальное вершинное покрытие=== | ===Минимальное вершинное покрытие=== | ||
{{Определение|neat=neat|definition= | {{Определение|neat=neat|definition= | ||
| − | '''Вершинным покрытием''' (англ. '''Vertex covering | + | '''Вершинным покрытием''' (англ. '''Vertex covering''') графа <tex>G=(V,E)</tex> называется такое подмножество <tex>S</tex> множества вершин графа <tex>V</tex>, что любое ребро этого графа инцидентно хотя бы одной вершине из множества <tex>S</tex>. |
}} | }} | ||
{{Определение|neat=neat|definition= | {{Определение|neat=neat|definition= | ||
| − | '''Минимальным вершинным покрытием''' (англ. '''Minimum vertex covering | + | '''Минимальным вершинным покрытием''' (англ. '''Minimum vertex covering''') графа <tex>G=(V,E)</tex> называется вершинное покрытие, состоящее из наименьшего числа вершин. |
}} | }} | ||
<br/> | <br/> | ||
| Строка 16: | Строка 16: | ||
==Пример== | ==Пример== | ||
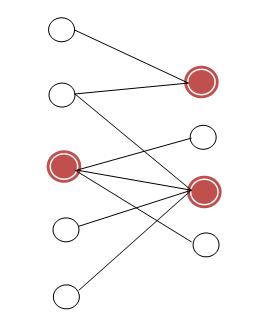
| − | [[Файл:Cover.jpg|300px | + | [[Файл:Cover.jpg|thumb|left|300px|Множество вершин красного цвета — минимальное вершинное покрытие.]] |
| − | |||
| − | Множество вершин красного цвета — минимальное вершинное покрытие. | ||
| − | |||
| − | |||
<br/> | <br/> | ||
| + | <br/><br/><br/><br/><br/> | ||
| + | <br/><br/><br/><br/><br/> | ||
| + | <br/><br/><br/><br/><br/> | ||
| + | <br/><br/><br/><br/><br/> | ||
==Связь максимального паросочетания и минимального вершинного покрытия в двудольном графе== | ==Связь максимального паросочетания и минимального вершинного покрытия в двудольном графе== | ||
| − | === | + | ===Теорема о мощности минимального вершинного покрытия и максимального паросочетания=== |
{{Определение|definition= | {{Определение|definition= | ||
| − | '''Максимальным''' [[Теорема_о_максимальном_паросочетании_и_дополняющих_цепях|'''паросочетанием''']] (англ. '''Maximum matching | + | '''Максимальным''' [[Теорема_о_максимальном_паросочетании_и_дополняющих_цепях|'''паросочетанием''']] (англ. '''Maximum matching''') в [[Двудольные графы и раскраска в 2 цвета|двудольном графе]] <tex>G</tex> называется паросочетание максимальной мощности. |
}} | }} | ||
| − | + | ||
{{Теорема|neat = neat|statement= | {{Теорема|neat = neat|statement= | ||
В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия. | В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия. | ||
| Строка 47: | Строка 47: | ||
В <tex>L^-</tex> свободных вершин быть не может, т.к. все они должны находиться в <tex>L^+</tex>. Тогда т.к. ребер из паросочетания между <tex>R^+</tex> | В <tex>L^-</tex> свободных вершин быть не может, т.к. все они должны находиться в <tex>L^+</tex>. Тогда т.к. ребер из паросочетания между <tex>R^+</tex> | ||
и <tex>L^-</tex> нет, то каждому ребру максимальным паросочетания инцидентна ровно одна вершина из <tex>L^- \cup R^+</tex>. | и <tex>L^-</tex> нет, то каждому ребру максимальным паросочетания инцидентна ровно одна вершина из <tex>L^- \cup R^+</tex>. | ||
| − | Тогда <tex>|L^- \cup R^+ | + | Тогда <tex>|L^- \cup R^+|</tex> равна мощности максимального паросочетания. Множество вершин <tex>L^- \cup R^+</tex> является минимальным вершинным покрытием. Значит мощность максимального паросочетания равна мощности минимального вершинного покрытия. |
}} | }} | ||
| Строка 60: | Строка 60: | ||
==См. также == | ==См. также == | ||
| + | [[Теорема_о_максимальном_паросочетании_и_дополняющих_цепях|Теорема о максимальном паросочетании и дополняющих цепях]]. | ||
| + | <br> | ||
[[Связь_вершинного_покрытия_и_независимого_множества|Связь вершинного покрытия и независимого множества]]. | [[Связь_вершинного_покрытия_и_независимого_множества|Связь вершинного покрытия и независимого множества]]. | ||
Версия 19:57, 10 марта 2012
Содержание
Определения
Минимальное вершинное покрытие
Пример
Связь максимального паросочетания и минимального вершинного покрытия в двудольном графе
Теорема о мощности минимального вершинного покрытия и максимального паросочетания
| Определение: |
| Максимальным паросочетанием (англ. Maximum matching) в двудольном графе называется паросочетание максимальной мощности. |
| Теорема: |
В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия. |
| Доказательство: |
|
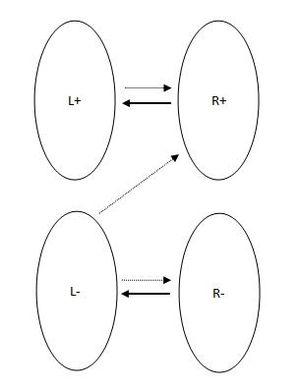
Пусть в построено максимальное паросочетание. Ориентируем ребра паросочетания, чтобы они шли из правой доли в левую, ребра не из паросочетания — так, чтобы они шли из левой доли в правую. Запустим обход в глубину из всех не насыщенных паросочетанием вершин левой доли. Разобьем вершины каждой доли графа на два множества: те, которые были посещены в процессе обхода, и те, которые не были посещены в процессе обхода. Тогда , , где — правая и левая доли соответственно, — вершины правой и левой доли, посещенные обходом, — не посещенные обходом вершины. Тогда в могут быть следующие ребра:
Очевидно, что ребер из в и из из в быть не может. Ребер из из в быть не может, т.к. если такое ребро существует, то оно — ребро паросочетания. Тогда вершина насыщена паросочетанием. Но т.к. , то в нее можно дойти из какой-то ненасыщенной вершины левой доли. Значит, существует ребро . Но тогда инцидентны два ребра из паросочетания. Противоречие. Заметим, что минимальным вершинным покрытием является либо , либо , либо . В не насыщенных паросочетанием вершин быть не может, т.к. иначе в существует дополняющая цепь, что противоречит максимальности построенного паросочетания. В свободных вершин быть не может, т.к. все они должны находиться в . Тогда т.к. ребер из паросочетания между и нет, то каждому ребру максимальным паросочетания инцидентна ровно одна вершина из . Тогда равна мощности максимального паросочетания. Множество вершин является минимальным вершинным покрытием. Значит мощность максимального паросочетания равна мощности минимального вершинного покрытия. |
Алгоритм построения минимального вершинного покрытия
Из доказательства предыдущей теоремы следует алгоритм поиска минимального вершинного покрытия графа:
- Построить максимальное паросочетание.
- Ориентировать ребра:
- Из паросочетания — из правой доли в левую.
- Не из паросочетания — из левой доли в правую.
- Запустить обход в глубину из всех свободных вершин левой доли, построить множества .
- В качестве результата взять .
См. также
Теорема о максимальном паросочетании и дополняющих цепях.
Связь вершинного покрытия и независимого множества.
Источники
1. Теорема Кёнига.