Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах — различия между версиями
| Строка 20: | Строка 20: | ||
|proof= | |proof= | ||
Пусть в <tex>G</tex> построено максимальное паросочетание. Ориентируем ребра паросочетания, чтобы они шли из правой доли в левую, ребра не из паросочетания --- так, чтобы они шли из левой доли в правую. Запустим обход в глубину из всех не насыщенных паросочетанием вершин левой доли. Разобьем вершины каждой доли графа на два множества: те, которые были посещены в процессе обхода, и те, которые не были посещены в процессе обхода. | Пусть в <tex>G</tex> построено максимальное паросочетание. Ориентируем ребра паросочетания, чтобы они шли из правой доли в левую, ребра не из паросочетания --- так, чтобы они шли из левой доли в правую. Запустим обход в глубину из всех не насыщенных паросочетанием вершин левой доли. Разобьем вершины каждой доли графа на два множества: те, которые были посещены в процессе обхода, и те, которые не были посещены в процессе обхода. | ||
| − | Тогда <tex>L = | + | Тогда <tex>L = L^+ \cup L^-</tex>, <tex>R = R^+ \cup R^-</tex>, где <tex>L, R</tex> --- правая и левая доли соответственно, <tex>L^+, R^+</tex> --- вершины правой и левой доли, посещенные обходом, <tex>L^-, R^-</tex> --- не посещенные обходом вершины. |
Тогда в <tex>G</tex> могут быть следующие ребра: | Тогда в <tex>G</tex> могут быть следующие ребра: | ||
| − | *Из вершин <tex> | + | *Из вершин <tex>L^+</tex> в вершины <tex>R^+</tex> и из вершин <tex>R^+</tex> в вершины <tex>L^+</tex>. |
| − | *Из вершин <tex> | + | *Из вершин <tex>L^-</tex> в вершины <tex>R^-</tex> и из вершин <tex>R^-</tex> в вершины <tex>L^-</tex>. |
| − | *Из вершин <tex> | + | *Из вершин <tex>L^-</tex> в вершины <tex>R^+</tex>. |
| − | Очевидно, что ребер из <tex> | + | Очевидно, что ребер из <tex>L^+</tex> в <tex>R^-</tex> и из из <tex>R^+</tex> в <tex>L^-</tex> быть не может. |
| − | Ребер из из <tex> | + | Ребер из из <tex>R^-</tex> в <tex>L^+</tex> быть не может, т.к. если такое ребро <tex>uv</tex> существует, то оно --- ребро паросочетания. Тогда вершина <tex>v</tex> насыщена паросочетанием. Но т.к. <tex>v \in L^+</tex>, то в нее можно дойти из какой-то ненасыщенной вершины левой доли. Значит, существует ребро <tex>wv, w \in R^+</tex>. Но тогда <tex>v</tex> инцидентны два ребра из паросочетания. Противоречие. |
| − | Заметим, что минимальным вершинным покрытием <tex>G</tex> является либо <tex>L</tex>, либо <tex>R</tex>, либо <tex> | + | Заметим, что минимальным вершинным покрытием <tex>G</tex> является либо <tex>L</tex>, либо <tex>R</tex>, либо <tex>L^- \cup R^+</tex>. |
| − | В <tex> | + | В <tex>R^+</tex> не насыщенных паросочетанием вершин быть не может, т.к. иначе в <tex>G</tex> существует дополняющая цепь, что противоречит максимальности построенного паросочетания. |
| − | В <tex> | + | В <tex>L^-</tex> свободных вершин быть не может, т.к. все они должны находиться в <tex>L^+</tex>. Тогда т.к. ребер из паросочетания между <tex>R^+</tex> |
| − | и <tex> | + | и <tex>L^-</tex> нет, то каждому ребру <tex>MM</tex> инцидентна ровно одна вершина из <tex>L^- \cup R^+</tex>. |
| − | Тогда <tex>| | + | Тогда <tex>|L^- \cup R^+| = |MM| \le min(|L|, |R|)</tex>. Значит, <tex>|MVC| = |MM|</tex>. |
}} | }} | ||
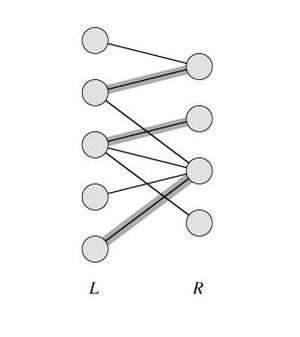
[[Файл:Matching.jpg|thumb|right|Пример максимального паросочетания]] | [[Файл:Matching.jpg|thumb|right|Пример максимального паросочетания]] | ||
Версия 16:53, 15 декабря 2010
Определения
| Определение: |
| Паросочетанием в графе называется такое подмножество множества ребер графа ,
что каждая вершина инцидентна не более чем одному ребру из . |
| Определение: |
| Максимальным паросочетанием в графе называется паросочетание максимальной мощности. |
| Определение: |
| Вершинным покрытием графа называется такое подмножество множества вершин графа , что каждому ребру инцидентна хотя бы одна вершина из . |
| Определение: |
| Минимальным вершинным покрытием графа называется вершинное покрытие минимальной мощности. |
Связь MM и MVC в двудольном графе
| Теорема: |
В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия. |
| Доказательство: |
|
Пусть в построено максимальное паросочетание. Ориентируем ребра паросочетания, чтобы они шли из правой доли в левую, ребра не из паросочетания --- так, чтобы они шли из левой доли в правую. Запустим обход в глубину из всех не насыщенных паросочетанием вершин левой доли. Разобьем вершины каждой доли графа на два множества: те, которые были посещены в процессе обхода, и те, которые не были посещены в процессе обхода. Тогда , , где --- правая и левая доли соответственно, --- вершины правой и левой доли, посещенные обходом, --- не посещенные обходом вершины. Тогда в могут быть следующие ребра:
Очевидно, что ребер из в и из из в быть не может. Ребер из из в быть не может, т.к. если такое ребро существует, то оно --- ребро паросочетания. Тогда вершина насыщена паросочетанием. Но т.к. , то в нее можно дойти из какой-то ненасыщенной вершины левой доли. Значит, существует ребро . Но тогда инцидентны два ребра из паросочетания. Противоречие. Заметим, что минимальным вершинным покрытием является либо , либо , либо . В не насыщенных паросочетанием вершин быть не может, т.к. иначе в существует дополняющая цепь, что противоречит максимальности построенного паросочетания. В свободных вершин быть не может, т.к. все они должны находиться в . Тогда т.к. ребер из паросочетания между и нет, то каждому ребру инцидентна ровно одна вершина из . Тогда . Значит, . |