Сортировка Хана — различия между версиями
Sultan (обсуждение | вклад) м (→Andersson's exponential search tree) |
6yry6e (обсуждение | вклад) |
||
| (не показано 14 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Сортировка Хана ( | + | '''Сортировка Хана''' (англ. ''Hansort'') {{---}} сложный алгоритм сортировки целых чисел со сложностью <tex dpi="130">O(n \log\log n)</tex>, где <tex dpi="130">n</tex> {{---}} количество элементов для сортировки. |
| − | Данная статья писалась на основе брошюры Хана, посвященной этой сортировке. | + | Данная статья писалась на основе брошюры Хана (англ. ''Yijie Han''), посвященной этой сортировке. |
== Описание == | == Описание == | ||
| − | Алгоритм построен на основе экспоненциального поискового дерева | + | Алгоритм построен на основе '''экспоненциального поискового дерева Андерсона''' (англ. ''Andersson's exponential search tree''). Сортировка происходит за счет вставки целых чисел в экспоненциальное поисковое дерево (''далее {{---}} ЭП-дерево''). |
| − | == | + | == Экспоненциальное поисковое дерево Андерсона == |
{{Определение | {{Определение | ||
| − | |definition = ЭП-дерево - это дерево поиска, в котором все ключи хранятся в листьях этого дерева и количество детей у каждого узла уменьшается экспоненциально от глубины узла. | + | |definition = '''ЭП-дерево''' {{---}} это дерево поиска, в котором все ключи хранятся в листьях этого дерева и количество детей у каждого узла уменьшается экспоненциально от глубины узла. |
}} | }} | ||
| Строка 16: | Строка 16: | ||
Структура ЭП-дерева: | Структура ЭП-дерева: | ||
| − | 1) Корень имеет <tex>\Theta (n^e)</tex> сыновей | + | 1) Корень имеет <tex dpi="130">\Theta (n^e)</tex> сыновей <tex dpi="130">( 0 < e < 1 )</tex>. Все сыновья являются ЭП-деревьями. |
| − | 2) Каждое поддерево корня имеет <tex>\Theta(n^{1-e})</tex> сыновей. | + | 2) Каждое поддерево корня имеет <tex dpi="130">\Theta(n^{1-e})</tex> сыновей. |
| − | В этом дереве <tex>O(n \log\log n)</tex> уровней. При нарушении баланса дерева необходимо балансирование, которое требует <tex>O(n \log\log n)</tex> времени при <tex>n</tex> вставленных целых числах. Такое время достигается за счет вставки чисел группами, а не поодиночке, как изначально предлагал Андерссон. | + | В этом дереве <tex dpi="130">O(n \log\log n)</tex> уровней. При нарушении баланса дерева необходимо балансирование, которое требует <tex dpi="130">O(n \log\log n)</tex> времени при <tex dpi="130">n</tex> вставленных целых числах. Такое время достигается за счет вставки чисел группами, а не поодиночке, как изначально предлагал Андерссон. |
==Определения== | ==Определения== | ||
| Строка 26: | Строка 26: | ||
'''Контейнер''' {{---}} объект, в которым хранятся наши данные. Например: 32-битные и 64-битные числа, массивы, вектора.}} | '''Контейнер''' {{---}} объект, в которым хранятся наши данные. Например: 32-битные и 64-битные числа, массивы, вектора.}} | ||
{{ Определение | definition = | {{ Определение | definition = | ||
| − | Алгоритм, сортирующий <tex>n</tex> целых чисел из множества <tex>\{0, 1, \ldots, m - 1\}</tex>, называется '''консервативным''', если длина контейнера (число бит в контейнере) равна <tex>O(\log(m + n))</tex>. Если длина больше, то алгоритм '''неконсервативный'''. | + | Алгоритм, сортирующий <tex dpi="130">n</tex> целых чисел из множества <tex dpi="130">\{0, 1, \ldots, m - 1\}</tex>, называется '''консервативным''', если длина контейнера (число бит в контейнере) равна <tex dpi="130">O(\log(m + n))</tex>. Если длина больше, то алгоритм '''неконсервативный'''. |
}} | }} | ||
{{ Определение | definition = | {{ Определение | definition = | ||
| − | Если сортируются целые числа из множества <tex>\{0, 1, \ldots, m - 1\}</tex> с длиной контейнера <tex>k \log (m + n)</tex> с <tex>k | + | Если сортируются целые числа из множества <tex dpi="130">\{0, 1, \ldots, m - 1\}</tex> с длиной контейнера <tex dpi="130">k \log (m + n)</tex> с <tex dpi="130">k \geqslant 1</tex>, тогда сортировка происходит с '''неконсервативным преимуществом''' <tex dpi="130">k</tex>. |
}} | }} | ||
{{ Определение | definition = | {{ Определение | definition = | ||
| − | Для множества <tex>S</tex> определим | + | Для множества <tex dpi="130">S</tex> определим |
| − | <tex>\min(S) = \min\limits_{a \in S} a</tex> | + | <tex dpi="130">\min(S) = \min\limits_{a \in S} a</tex> |
| − | <tex>\max(S) = \max\limits_{a \in S} a</tex> | + | <tex dpi="130">\max(S) = \max\limits_{a \in S} a</tex> |
| − | Набор <tex>S1< | + | Набор <tex dpi="130">S1 < S2</tex> если <tex dpi="130">\max(S1) \leqslant \min(S2)</tex> |
}} | }} | ||
{{ Определение | definition = | {{ Определение | definition = | ||
| − | Предположим, есть набор <tex>T</tex> из <tex>p</tex> чисел, которые уже отсортированы как <tex>a_{1}, a_{2}, \ldots, a_{p}</tex> и набор <tex>S</tex> из <tex>q</tex> чисел <tex>b_{1}, b_{2}, \ldots, b_{q}</tex>. Тогда '''разделением''' <tex>q</tex> чисел <tex>p</tex> числами называется <tex>p + 1</tex> набор <tex>S_{0}, S_{1}, \ldots, S_{p}</tex>, где <tex>S_{0}< | + | Предположим, есть набор <tex dpi="130">T</tex> из <tex dpi="130">p</tex> чисел, которые уже отсортированы как <tex dpi="130">a_{1}, a_{2}, \ldots, a_{p}</tex> и набор <tex dpi="130">S</tex> из <tex dpi="130">q</tex> чисел <tex dpi="130">b_{1}, b_{2}, \ldots, b_{q}</tex>. Тогда '''разделением''' <tex dpi="130">q</tex> чисел <tex dpi="130">p</tex> числами называется <tex dpi="130">p + 1</tex> набор <tex dpi="130">S_{0}, S_{1}, \ldots, S_{p}</tex>, где <tex dpi="130">S_{0} < a_{1} < S_{1} < \ldots < a_{p} < S_{p}</tex>. |
}} | }} | ||
| Строка 51: | Строка 51: | ||
|about = № 1 | |about = № 1 | ||
|statement = | |statement = | ||
| − | Даны целые числа <tex>b | + | Даны целые числа <tex dpi="130">b \geqslant s \geqslant 0</tex>, и <tex dpi="130">T</tex> является подмножеством множества <tex dpi="130">\{0, \ldots, 2^b - 1\}</tex>, содержащим <tex dpi="130">n</tex> элементов, и <tex dpi="130">t \geqslant 2^{-s + 1}С^k_{n}</tex>. Функция <tex dpi="130">h_{a}</tex>, принадлежащая <tex dpi="130">H_{b,s}</tex>, может быть выбрана за время <tex dpi="130">O(bn^2)</tex> так, что количество коллизий <tex dpi="130">coll(h_{a}, T) \leqslant t</tex>. |
}} | }} | ||
| Строка 58: | Строка 58: | ||
|about = № 2 | |about = № 2 | ||
|statement = | |statement = | ||
| − | Выбор <tex>s</tex>-ого наибольшего числа среди <tex>n</tex> чисел, упакованных в <tex>n | + | Выбор <tex dpi="130">s</tex>-ого наибольшего числа среди <tex dpi="130">n</tex> чисел, упакованных в <tex dpi="150">\frac{n}{g}</tex> контейнеров, может быть сделан за время <tex dpi="150">O(\frac{n \log g}{g})</tex> и с использованием <tex dpi="150">O(\frac{n}{g})</tex> памяти. В том числе, так может быть найдена медиана. |
|proof = | |proof = | ||
| − | Так как возможно делать попарное сравнение <tex>g</tex> чисел в одном контейнере с <tex>g</tex> числами в другом и извлекать большие числа из одного контейнера и меньшие из другого за константное время, возможно упаковать медианы из первого, второго, <tex>\ldots</tex>, <tex>g</tex>-ого чисел из 5 контейнеров в один контейнер за константное время. Таким образом, набор <tex>S</tex> из медиан теперь содержится в <tex>n | + | Так как возможно делать попарное сравнение <tex dpi="130">g</tex> чисел в одном контейнере с <tex dpi="130">g</tex> числами в другом и извлекать большие числа из одного контейнера и меньшие из другого за константное время, возможно упаковать медианы из первого, второго, <tex dpi="130">\ldots</tex>, <tex dpi="130">g</tex>-ого чисел из 5 контейнеров в один контейнер за константное время. Таким образом, набор <tex dpi="130">S</tex> из медиан теперь содержится в <tex dpi="150">\frac{n}{5g}</tex> контейнерах. Рекурсивно находим медиану <tex dpi="130">m</tex> в <tex dpi="130">S</tex>. Используя <tex dpi="130">m</tex>, уберем хотя бы <tex dpi="150">\frac{n}{4}</tex> чисел среди <tex dpi="130">n</tex>. Затем упакуем оставшиеся из <tex dpi="150">\frac{n}{g}</tex> контейнеров в <tex dpi="150">\frac{3n}{4g}</tex> контейнеров и затем продолжим рекурсию. |
}} | }} | ||
| Строка 68: | Строка 68: | ||
|about = № 3 | |about = № 3 | ||
|statement = | |statement = | ||
| − | Если <tex>g</tex> целых чисел, в сумме использующих <tex> | + | Если <tex dpi="130">g</tex> целых чисел, в сумме использующих <tex dpi="150">\frac{\log n}{2}</tex> бит, упакованы в один контейнер, тогда <tex dpi="130">n</tex> чисел в <tex dpi="150">\frac{n}{g}</tex> контейнерах могут быть отсортированы за время <tex dpi="150">O(\frac{n \log g}{g})</tex> с использованием <tex dpi="150">O(\frac{n}{g})</tex> памяти. |
|proof = | |proof = | ||
| − | Так как используется только <tex> | + | Так как используется только <tex dpi="150">\frac{\log n}{2}</tex> бит в каждом контейнере для хранения <tex dpi="130">g</tex> чисел, используем bucket sort, чтобы отсортировать все контейнеры, представляя каждый как число, что занимает <tex dpi="150">O(\frac{n}{g})</tex> времени и памяти. Так как используется <tex dpi="150">\frac{\log n}{2}</tex> бит на контейнер, понадобится <tex dpi="130">\sqrt{n}</tex> шаблонов для всех контейнеров. Затем поместим <tex dpi="150">g < \frac{\log n}{2}</tex> контейнеров с одинаковым шаблоном в одну группу. Для каждого шаблона останется не более <tex dpi="130">g - 1</tex> контейнеров, которые не смогут образовать группу. Поэтому не более <tex dpi="130">\sqrt{n}(g - 1)</tex> контейнеров не смогут сформировать группу. Для каждой группы помещаем <tex dpi="130">i</tex>-е число во всех <tex dpi="130">g</tex> контейнерах в один. Таким образом берутся <tex dpi="130">g</tex> <tex dpi="130">g</tex>-целых векторов и получаются <tex dpi="130">g</tex> <tex dpi="130">g</tex>-целых векторов, где <tex dpi="130">i</tex>-ый вектор содержит <tex dpi="130">i</tex>-ое число из входящего вектора. Эта транспозиция может быть сделана за время <tex dpi="130">O(g \log g)</tex>, с использованием <tex dpi="130">O(g)</tex> памяти. Для всех групп это занимает время <tex dpi="150">O(\frac{n \log g}{g})</tex>, с использованием <tex dpi="150">O(\frac{n}{g})</tex> памяти. |
| − | Для контейнеров вне групп (которых <tex>\sqrt{n}(g - 1)</tex> штук) разбираем и собираем заново контейнеры. На это потребуется не более <tex>O(n | + | Для контейнеров вне групп (которых <tex dpi="130">\sqrt{n}(g - 1)</tex> штук) разбираем и собираем заново контейнеры. На это потребуется не более <tex dpi="150">O(\frac{n}{g})</tex> времени и памяти. После всего этого используем карманную сортировку вновь для сортировки <tex dpi="130">n</tex> контейнеров. Таким образом, все числа отсортированы. |
| − | Заметим, что когда <tex>g = O( \log n)</tex>, сортировка <tex>O(n)</tex> чисел в <tex>n | + | Заметим, что когда <tex dpi="130">g = O( \log n)</tex>, сортировка <tex dpi="130">O(n)</tex> чисел в <tex dpi="150">\frac{n}{g}</tex> контейнеров произойдет за время <tex dpi="150">O((\frac{n}{g})</tex> <tex dpi="130">\log\log n)</tex> с использованием <tex dpi="150">O(\frac{n}{g})</tex> памяти. Выгода очевидна. |
}} | }} | ||
| Строка 84: | Строка 84: | ||
|about = № 4 | |about = № 4 | ||
|statement = | |statement = | ||
| − | Примем, что каждый контейнер содержит <tex> \log m > \log n</tex> бит, и <tex>g</tex> чисел, в каждом из которых <tex> | + | Примем, что каждый контейнер содержит <tex dpi="130"> \log m > \log n</tex> бит, и <tex dpi="130">g</tex> чисел, в каждом из которых <tex dpi="150">\frac{\log m}{g}</tex> бит, упакованы в один контейнер. Если каждое число имеет маркер, содержащий <tex dpi="150">\frac{\log n}{2g}</tex> бит, и <tex dpi="130">g</tex> маркеров упакованы в один контейнер таким же образом<tex dpi="130">^*</tex>, что и числа, тогда <tex dpi="130">n</tex> чисел в <tex dpi="150">\frac{n}{g}</tex> контейнерах могут быть отсортированы по их маркерам за время <tex dpi="150">O(\frac{n \log\log n}{g})</tex> с использованием <tex dpi="150">O(\frac{n}{g})</tex> памяти. |
| − | (*): если число <tex>a</tex> упаковано как <tex>s</tex>-ое число в <tex>t</tex>-ом контейнере для чисел, тогда маркер для <tex>a</tex> упакован как <tex>s</tex>-ый маркер в <tex>t</tex>-ом контейнере для маркеров. | + | (*): если число <tex dpi="130">a</tex> упаковано как <tex dpi="130">s</tex>-ое число в <tex dpi="130">t</tex>-ом контейнере для чисел, тогда маркер для <tex dpi="130">a</tex> упакован как <tex dpi="130">s</tex>-ый маркер в <tex dpi="130">t</tex>-ом контейнере для маркеров. |
|proof = | |proof = | ||
| − | Контейнеры для маркеров могут быть отсортированы с помощью bucket sort потому, что каждый контейнер использует <tex> | + | Контейнеры для маркеров могут быть отсортированы с помощью bucket sort потому, что каждый контейнер использует <tex dpi="150">\frac{\log n}{2}</tex> бит. Сортировка сгруппирует контейнеры для чисел как в [[#lemma3|лемме №3]]. Перемещаем каждую группу контейнеров для чисел. |
}} | }} | ||
| Строка 96: | Строка 96: | ||
|about = № 5 | |about = № 5 | ||
|statement = | |statement = | ||
| − | Предположим, что каждый контейнер содержит <tex>\log m \log\log n > \log n</tex> бит, что <tex>g</tex> чисел, в каждом из которых <tex> | + | Предположим, что каждый контейнер содержит <tex dpi="130">\log m \log\log n > \log n</tex> бит, что <tex dpi="130">g</tex> чисел, в каждом из которых <tex dpi="150">\frac{\log m}{g}</tex> бит, упакованы в один контейнер, что каждое число имеет маркер, содержащий <tex dpi="150">\frac{\log n}{2g}</tex> бит, и что <tex dpi="130">g</tex> маркеров упакованы в один контейнер тем же образом что и числа. Тогда <tex dpi="130">n</tex> чисел в <tex dpi="150">\frac{n}{g}</tex> контейнерах могут быть отсортированы по своим маркерам за время <tex dpi="150">O(\frac{n}{g})</tex> с использованием <tex dpi="150">O(\frac{n}{g})</tex> памяти. |
|proof = | |proof = | ||
| − | Заметим, что несмотря на то, что длина контейнера <tex>\log m \log\log n</tex> бит, всего <tex>\log m</tex> бит используется для хранения упакованных чисел. Так же как в [[#lemma3|лемме №3]] и [[#lemma4|лемме №4]] сортируем контейнеры упакованных маркеров с помощью bucket sort. Для того, чтобы перемещать контейнеры чисел, помещаем <tex>g \log\log n</tex> вместо <tex>g</tex> контейнеров чисел в одну группу. Для транспозиции чисел в группе, содержащей <tex>g \log\log n</tex> контейнеров, упаковываем <tex>g \log\log n</tex> контейнеров в <tex>g</tex>, упаковывая <tex>\log\log n</tex> контейнеров в один. Далее делаем транспозицию над <tex>g</tex> контейнерами. Таким образом перемещение занимает всего <tex>O(g \log\log n)</tex> времени для каждой группы и <tex>O(n | + | Заметим, что несмотря на то, что длина контейнера <tex dpi="130">\log m \log\log n</tex> бит, всего <tex dpi="130">\log m</tex> бит используется для хранения упакованных чисел. Так же как в [[#lemma3|лемме №3]] и [[#lemma4|лемме №4]] сортируем контейнеры упакованных маркеров с помощью bucket sort. Для того, чтобы перемещать контейнеры чисел, помещаем <tex dpi="130">g \log\log n</tex> вместо <tex dpi="130">g</tex> контейнеров чисел в одну группу. Для транспозиции чисел в группе, содержащей <tex dpi="130">g \log\log n</tex> контейнеров, упаковываем <tex dpi="130">g \log\log n</tex> контейнеров в <tex dpi="130">g</tex>, упаковывая <tex dpi="130">\log\log n</tex> контейнеров в один. Далее делаем транспозицию над <tex dpi="130">g</tex> контейнерами. Таким образом перемещение занимает всего <tex dpi="130">O(g \log\log n)</tex> времени для каждой группы и <tex dpi="150">O(\frac{n}{g})</tex> времени для всех чисел. После завершения транспозиции, распаковываем <tex dpi="130">g</tex> контейнеров в <tex dpi="130">g \log\log n</tex> контейнеров. |
| − | Заметим, что если длина контейнера <tex>\log m \log\log n</tex> и только <tex>\log m</tex> бит используется для упаковки <tex>g \ | + | Заметим, что если длина контейнера <tex dpi="130">\log m \log\log n</tex> и только <tex dpi="130">\log m</tex> бит используется для упаковки <tex dpi="130">g \leqslant \log n</tex> чисел в один контейнер, тогда выбор в [[#lemma2|лемме №2]] может быть сделан за время и память <tex dpi="150">O(\frac{n}{g})</tex>, потому что упаковка в доказательстве [[#lemma2|лемме №2]] теперь может быть сделана за время <tex dpi="150">O(\frac{n}{g})</tex>. |
}} | }} | ||
| Строка 110: | Строка 110: | ||
|about = № 6 | |about = № 6 | ||
|statement = | |statement = | ||
| − | <tex>n</tex> целых чисел можно отсортировать в <tex>\sqrt{n}</tex> наборов <tex>S_{1}</tex>, <tex>S_{2}</tex>, <tex>\ldots</tex>, <tex>S_{\sqrt{n}}</tex> таким образом, что в каждом наборе <tex>\sqrt{n}</tex> чисел и <tex>S_{i}< | + | <tex dpi="130">n</tex> целых чисел можно отсортировать в <tex dpi="130">\sqrt{n}</tex> наборов <tex dpi="130">S_{1}</tex>, <tex dpi="130">S_{2}</tex>, <tex dpi="130">\ldots</tex>, <tex dpi="130">S_{\sqrt{n}}</tex> таким образом, что в каждом наборе <tex dpi="130">\sqrt{n}</tex> чисел и <tex dpi="130">S_{i} < S_{j}</tex> при <tex dpi="130">i < j</tex>, за время <tex dpi="150">O(\frac{n \log\log n} {\log k})</tex> и место <tex dpi="130">O(n)</tex> с неконсервативным преимуществом <tex dpi="130">k \log\log n</tex>. |
|proof = | |proof = | ||
| − | Алгоритм сортировки <tex>n</tex> целых чисел в <tex>\sqrt{n}</tex> наборов, представленный ниже, является доказательством данной леммы. | + | Алгоритм сортировки <tex dpi="130">n</tex> целых чисел в <tex dpi="130">\sqrt{n}</tex> наборов, представленный ниже, является доказательством данной леммы. |
Постановка задачи и решение некоторых проблем: | Постановка задачи и решение некоторых проблем: | ||
| − | Рассмотрим проблему сортировки <tex>n</tex> целых чисел из множества <tex>\{0, 1, \ldots, m - 1\}</tex> в <tex>\sqrt{n}</tex> наборов, как в условии леммы. Предполагаем, что каждый контейнер содержит <tex>k \log\log n \log m</tex> бит и хранит число в <tex>\log m</tex> бит. Поэтому неконсервативное преимущество {{---}} <tex>k \log \log n</tex>. Также предполагаем, что <tex>\log m \ | + | Рассмотрим проблему сортировки <tex dpi="130">n</tex> целых чисел из множества <tex dpi="130">\{0, 1, \ldots, m - 1\}</tex> в <tex dpi="130">\sqrt{n}</tex> наборов, как в условии леммы. Предполагаем, что каждый контейнер содержит <tex dpi="130">k \log\log n \log m</tex> бит и хранит число в <tex dpi="130">\log m</tex> бит. Поэтому неконсервативное преимущество {{---}} <tex dpi="130">k \log \log n</tex>. Также предполагаем, что <tex dpi="130">\log m \geqslant \log n \log\log n</tex>. Иначе можно использовать radix sort для сортировки за время <tex dpi="130">O(n \log\log n)</tex> и линейную память. Делим <tex dpi="130">\log m</tex> бит, используемых для представления каждого числа, в <tex dpi="130">\log n</tex> блоков. Таким образом, каждый блок содержит как минимум <tex dpi="130">\log\log n</tex> бит. <tex dpi="130">i</tex>-ый блок содержит с |
| + | <tex dpi="150">\frac{i \log m} {\log n}</tex>-ого по <tex dpi="150">(\frac{(i + 1) \log m} {\log n - 1})</tex>-ый биты. Биты считаются с наименьшего бита, начиная с нуля. Теперь у нас имеется <tex dpi="130">2 \log n</tex>-уровневый алгоритм, который работает следующим образом: | ||
| − | На каждой стадии работаем с одним блоком бит. Назовем эти блоки маленькими числами (далее м.ч.), потому что каждое м.ч. теперь содержит только <tex>\log m | + | На каждой стадии работаем с одним блоком бит. Назовем эти блоки маленькими числами (далее м.ч.), потому что каждое м.ч. теперь содержит только <tex dpi="150">\frac{\log m}{\log n}</tex> бит. Каждое число представлено и соотносится с м.ч., над которым работаем в данный момент. Положим, что нулевая стадия работает с самым большим блоком (блок номер <tex dpi="130">\log n - 1</tex>). Предполагаем, что биты этих м.ч. упакованы в <tex dpi="150">\frac{n}{\log n}</tex> контейнеров с <tex dpi="130">\log n</tex> м.ч. упакованными в один контейнер. Пренебрегая временем, потраченным на эту упаковку, считаем, что она бесплатна. По [[#lemma2|лемме №2]] находим медиану этих <tex dpi="130">n</tex> м.ч. за время и память <tex dpi="150">O(\frac{n}{\log n})</tex>. Пусть <tex dpi="130">a</tex> {{---}} это найденная медиана. Тогда <tex dpi="130">n</tex> м.ч. могут быть разделены на не более чем три группы: <tex dpi="130">S_{1}</tex>, <tex dpi="130">S_{2}</tex> и <tex dpi="130">S_{3}</tex>. <tex dpi="130">S_{1}</tex> содержит м.ч., которые меньше <tex dpi="130">a</tex>, <tex dpi="130">S_{2}</tex> содержит м.ч., равные <tex dpi="130">a</tex>, <tex dpi="130">S_{3}</tex> содержит м.ч., большие <tex dpi="130">a</tex>. Также мощность <tex dpi="130">S_{1}</tex> и <tex dpi="130">S_{3} </tex> не превосходит <tex dpi="130">n/2</tex>. Мощность <tex dpi="130">S_{2}</tex> может быть любой. Пусть <tex dpi="130">S'_{2}</tex> {{---}} это набор чисел, у которых наибольший блок находится в <tex dpi="130">S_{2}</tex>. Тогда убираем из дальнейшего рассмотрения <tex dpi="150">\frac{\log m}{\log n}</tex> бит (наибольший блок) из каждого числа, принадлежащего <tex dpi="130">S'_{2}</tex>. Таким образом, после первой стадии каждое число находится в наборе размера не большего половины размера начального набора или один из блоков в числе убран из дальнейшего рассмотрения. Так как в каждом числе только <tex dpi="130">\log n</tex> блоков, для каждого числа потребуется не более <tex dpi="130">\log n</tex> стадий, чтобы поместить его в набор половинного размера. За <tex dpi="130">2 \log n</tex> стадий все числа будут отсортированы. Так как на каждой стадии работаем с <tex dpi="150">\frac{n}{\log n}</tex> контейнерами, то игнорируя время, необходимое на упаковку м.ч. в контейнеры и помещение м.ч. в нужный набор, затрачивается <tex dpi="130">O(n)</tex> времени из-за <tex dpi="130">2 \log n</tex> стадий. |
| − | Сложная часть алгоритма заключается в том, как поместить м.ч. в набор, которому принадлежит соответствующее число, после предыдущих операций деления набора в нашем алгоритме. Предположим, что <tex>n</tex> чисел уже поделены в <tex>e</tex> наборов. Используем <tex>\log e</tex> битов чтобы сделать марки для каждого набора. Теперь используем [[#lemma5|лемме №5]]. Полный размер маркера для каждого контейнера должен быть <tex>\log n | + | Сложная часть алгоритма заключается в том, как поместить м.ч. в набор, которому принадлежит соответствующее число, после предыдущих операций деления набора в нашем алгоритме. Предположим, что <tex dpi="130">n</tex> чисел уже поделены в <tex dpi="130">e</tex> наборов. Используем <tex dpi="130">\log e</tex> битов чтобы сделать марки для каждого набора. Теперь используем [[#lemma5|лемме №5]]. Полный размер маркера для каждого контейнера должен быть <tex dpi="150">\frac{\log n}{2}</tex>, и маркер использует <tex dpi="130">\log e</tex> бит, значит количество маркеров <tex dpi="130">g</tex> в каждом контейнере должно быть не более <tex dpi="150">\frac{\log n}{2\log e}</tex>. В дальнейшем, так как <tex dpi="150">g = \frac{\log n}{2 \log e}</tex>, м.ч. должны влезать в контейнер. Каждый контейнер содержит <tex dpi="130">k \log\log n \log n</tex> блоков, каждое м.ч. может содержать <tex dpi="150">O(\frac{k \log n}{g}) = O(k \log e)</tex> блоков. Заметим, что используется неконсервативное преимущество в <tex dpi="130">\log\log n</tex> для [[#lemma5|лемме №5]] Поэтому предполагается, что <tex dpi="150">\frac{\log n}{2 \log e}</tex> м.ч., в каждом из которых <tex dpi="130">k \log e</tex> блоков битов числа, упакованны в один контейнер. Для каждого м.ч. используется маркер из <tex dpi="130">\log e</tex> бит, который показывает, к какому набору он принадлежит. Предполагаем, что маркеры так же упакованы в контейнеры, как и м.ч. Так как каждый контейнер для маркеров содержит <tex dpi="150">\frac{\log n}{2 \log e}</tex> маркеров, то для каждого контейнера требуется <tex dpi="150">\frac{\log n}{2}</tex> бит. Таким образом, [[#lemma5|лемма №5]] может быть применена для помещения м.ч. в наборы, которым они принадлежат. Так как используется <tex dpi="150">O(\frac{n \log e}{ \log n})</tex> контейнеров, то время, необходимое для помещения м.ч. в их наборы, равно <tex dpi="150">O(\frac{n \log e}{ \log n})</tex>. |
Стоит отметить, что процесс помещения нестабилен, т.к. основан на алгоритме из [[#lemma5|леммы №5]]. | Стоит отметить, что процесс помещения нестабилен, т.к. основан на алгоритме из [[#lemma5|леммы №5]]. | ||
| Строка 132: | Строка 133: | ||
При таком помещении сразу возникает следующая проблема. | При таком помещении сразу возникает следующая проблема. | ||
| − | Рассмотрим число <tex>a</tex>, которое является <tex>i</tex>-ым в наборе <tex>S</tex>. Рассмотрим блок <tex>a</tex> (назовем его <tex>a'</tex>), который является <tex>i</tex>-ым м.ч. в <tex>S</tex>. Когда используется вышеописанный метод перемещения нескольких следующих блоков <tex>a</tex> (назовем это <tex>a''</tex>) в <tex>S</tex>, <tex>a''</tex> просто перемещен на позицию в наборе <tex>S</tex>, но не обязательно на позицию <tex>i</tex> (где расположен <tex>a'</tex>). Если значение блока <tex>a'</tex> одинаково для всех чисел в <tex>S</tex>, то это не создаст проблемы потому, что блок одинаков вне зависимости от того в какое место в <tex>S</tex> помещен <tex>a''</tex>. Иначе у нас возникает проблема дальнейшей сортировки. Поэтому поступаем следующим образом: На каждой стадии числа в одном наборе работают на общем блоке, который назовем "текущий блок набора". Блоки, которые предшествуют текущему блоку содержат важные биты и идентичны для всех чисел в наборе. Когда помещаем больше бит в набор, последующие блоки помещаются в набор вместе с текущим блоком. Так вот, в вышеописанном процессе помещения предполагается, что самый значимый блок среди <tex>k \log e</tex> блоков {{---}} это текущий блок. Таким образом, после того, как эти <tex>k \log e</tex> блоков помещены в набор, изначальный текущий блок удаляется, потому что известно, что эти <tex>k \log e</tex> блоков перемещены в правильный набор, и нам не важно где находился начальный текущий блок. Тот текущий блок находится в перемещенных <tex>k \log e</tex> блоках. | + | Рассмотрим число <tex dpi="130">a</tex>, которое является <tex dpi="130">i</tex>-ым в наборе <tex dpi="130">S</tex>. Рассмотрим блок <tex dpi="130">a</tex> (назовем его <tex dpi="130">a'</tex>), который является <tex dpi="130">i</tex>-ым м.ч. в <tex dpi="130">S</tex>. Когда используется вышеописанный метод перемещения нескольких следующих блоков <tex dpi="130">a</tex> (назовем это <tex dpi="130">a''</tex>) в <tex dpi="130">S</tex>, <tex dpi="130">a''</tex> просто перемещен на позицию в наборе <tex dpi="130">S</tex>, но не обязательно на позицию <tex dpi="130">i</tex> (где расположен <tex dpi="130">a'</tex>). Если значение блока <tex dpi="130">a'</tex> одинаково для всех чисел в <tex dpi="130">S</tex>, то это не создаст проблемы потому, что блок одинаков вне зависимости от того в какое место в <tex dpi="130">S</tex> помещен <tex dpi="130">a''</tex>. Иначе у нас возникает проблема дальнейшей сортировки. Поэтому поступаем следующим образом: На каждой стадии числа в одном наборе работают на общем блоке, который назовем "текущий блок набора". Блоки, которые предшествуют текущему блоку содержат важные биты и идентичны для всех чисел в наборе. Когда помещаем больше бит в набор, последующие блоки помещаются в набор вместе с текущим блоком. Так вот, в вышеописанном процессе помещения предполагается, что самый значимый блок среди <tex dpi="130">k \log e</tex> блоков {{---}} это текущий блок. Таким образом, после того, как эти <tex dpi="130">k \log e</tex> блоков помещены в набор, изначальный текущий блок удаляется, потому что известно, что эти <tex dpi="130">k \log e</tex> блоков перемещены в правильный набор, и нам не важно где находился начальный текущий блок. Тот текущий блок находится в перемещенных <tex dpi="130">k \log e</tex> блоках. |
| − | Стоит отметить, что после нескольких уровней деления размер наборов станет маленьким. Леммы [[#lemma3|3]], [[#lemma4|4]], [[#lemma5|5]] расчитаны на не очень маленькие наборы. Но поскольку сортируется набор из <tex>n</tex> элементов в наборы размера <tex>\sqrt{n}</tex>, то проблем быть не должно. | + | Стоит отметить, что после нескольких уровней деления размер наборов станет маленьким. Леммы [[#lemma3|3]], [[#lemma4|4]], [[#lemma5|5]] расчитаны на не очень маленькие наборы. Но поскольку сортируется набор из <tex dpi="130">n</tex> элементов в наборы размера <tex dpi="130">\sqrt{n}</tex>, то проблем быть не должно. |
| − | + | ===Алгоритм сортировки=== | |
| + | Algorithm <tex>Sort(advantage</tex>, <tex>level</tex>, <tex>a_{0}</tex>, <tex>a_{1}</tex>, <tex>\ldots</tex>, <tex>a_{t}</tex>) | ||
| − | + | <tex>advantage</tex> {{---}} это неконсервативное преимущество равное <tex>k\log\log n</tex>, <tex>a_{i}</tex>-ые это входящие целые числа в наборе, которые надо отсортировать, <tex>level</tex> это уровень рекурсии. | |
| − | + | # Если <tex>level</tex> равен <tex>1</tex> тогда изучаем размер набора. Если размер меньше или равен <tex>\sqrt{n}</tex>, то <tex>return</tex>. Иначе делим этот набор в <tex>\leqslant</tex> 3 набора, используя [[#lemma2|лемму №2]], чтобы найти медиану, а затем используем [[#lemma5|лемму №5]] для сортировки. Для набора, где все элементы равны медиане, не рассматриваем текущий блок и текущим блоком делаем следующий. Создаем маркер, являющийся номером набора для каждого из чисел (0, 1 или 2). Затем направляем маркер для каждого числа назад к месту, где число находилось в начале. Также направляем двубитное число для каждого входного числа, указывающее на текущий блок. | |
| − | + | # От <tex dpi="130">u = 1</tex> до <tex dpi="130">k</tex> | |
| − | + | ## Упаковываем <tex dpi="130">a^{(u)}_{i}</tex>-ый в часть из <tex dpi="130">1/k</tex>-ых номеров контейнеров. Где <tex dpi="130">a^{(u)}_{i}</tex> содержит несколько непрерывных блоков, которые состоят из <tex dpi="150">\frac{1}{k}</tex>-ых битов <tex dpi="130">a_{i}</tex>. При этом у <tex dpi="130">a^{(u)}_{i}</tex> текущий блок это самый крупный блок. | |
| − | # От <tex>u = 1</tex> до <tex>k</tex> | + | ## Вызываем <tex>Sort(advantage</tex>, <tex>level - 1</tex>, <tex dpi="130">a^{(u)}_{0}</tex>, <tex dpi="130">a^{(u)}_{1}</tex>, <tex>\ldots</tex>, <tex dpi="130">a^{(u)}_{t}</tex>). Когда алгоритм возвращается из этой рекурсии, маркер, показывающий для каждого числа, к какому набору это число относится, уже направлен назад к месту, где число находится во входных данных. Число, имеющее наибольшее число бит в <tex dpi="130">a_{i}</tex>, показывающее на текущий блок в нем, так же направлено назад к <tex dpi="130">a_{i}</tex>. |
| − | ## Упаковываем <tex>a^{(u)}_{i}</tex>-ый в часть из <tex>1/k</tex>-ых номеров контейнеров. Где <tex>a^{(u)}_{i}</tex> содержит несколько непрерывных блоков, которые состоят из <tex>1 | + | ## Отправляем <tex dpi="130">a_{i}</tex>-ые к их наборам, используя [[#lemma5|лемму №5]]. |
| − | ## Вызываем | ||
| − | ## Отправляем <tex>a_{i}</tex>-ые к их наборам, используя [[#lemma5|лемму №5]]. | ||
Algorithm IterateSort | Algorithm IterateSort | ||
| − | Call | + | Call <tex>Sort(advantage</tex>, <tex dpi="130">\log_{k}((\log n)/4)</tex>, <tex dpi="130">a_{0}</tex>, <tex dpi="130">a_{1}</tex>, <tex dpi="130">\ldots</tex>, <tex dpi="130">a_{n - 1}</tex>); |
от 1 до 5 | от 1 до 5 | ||
| − | # Помещаем <tex>a_{i}</tex> в соответствующий набор с помощью bucket sort, потому что наборов около <tex>\sqrt{n}</tex>. | + | # Помещаем <tex dpi="130">a_{i}</tex> в соответствующий набор с помощью блочной сортировки (англ. ''bucket sort''), потому что наборов около <tex dpi="130">\sqrt{n}</tex>. |
| − | # Для каждого набора <tex>S = </tex>{<tex>a_{i_{0}}, a_{i_{1}}, \ldots, a_{i_{t}}</tex>}, если <tex>t > \sqrt{n}</tex>, вызываем | + | # Для каждого набора <tex dpi="130">S = </tex>{<tex dpi="130">a_{i_{0}}, a_{i_{1}}, \ldots, a_{i_{t}}</tex>}, если <tex dpi="130">t > \sqrt{n}</tex>, вызываем <tex>Sort(advantage</tex>, <tex dpi="130">\log_{k}(\frac{\log n}{4})</tex>, <tex dpi="130">a_{i_{0}}, a_{i_{1}}, \ldots, a_{i_{t}}</tex>). |
| − | Время работы алгоритма <tex>O(n \log\log n | + | Время работы алгоритма <tex dpi="150">O(\frac{n \log\log n}{\log k})</tex>, что доказывает лемму. |
}} | }} | ||
| − | |||
| − | |||
| − | + | ==Уменьшение числа бит в числах== | |
| + | Один из способов ускорить сортировку {{---}} уменьшить число бит в числе. Один из способов уменьшить число бит в числе {{---}} использовать деление пополам (эту идею впервые подал van Emde Boas). Деление пополам заключается в том, что количество оставшихся бит в числе уменьшается в 2 раза. Это быстрый способ, требующий <tex dpi="130">O(m)</tex> памяти. Для своего дерева Андерссон использует хеширование, что позволяет сократить количество памяти до <tex dpi="130">O(n)</tex>. Для того чтобы еще ускорить алгоритм, необходимо упаковать несколько чисел в один контейнер, чтобы затем за константное количество шагов произвести хеширование для всех чисел, хранимых в контейнере. Для этого используется хеш-функция для хеширования <tex dpi="130">n</tex> чисел в таблицу размера <tex dpi="130">O(n^2)</tex> за константное время без коллизий. Для этого используется модифицированная хеш-функция авторства: Dierzfelbinger и Raman. | ||
| − | |||
| + | Алгоритм: Пусть целое число <tex dpi="130">b \geqslant 0</tex> и пусть <tex dpi="130">U = \{0, \ldots, 2^b - 1\}</tex>. Класс <tex dpi="130">H_{b,s}</tex> хеш-функций из <tex dpi="130">U</tex> в <tex dpi="130">\{0, \ldots, 2^s - 1\}</tex> определен как <tex dpi="130">H_{b,s} = \{h_{a} \mid 0 < a < 2^b, a \equiv 1 (\bmod 2)\}</tex> и для всех <tex dpi="130">x</tex> из <tex dpi="130">U</tex>: <tex dpi="130">h_{a}(x) = (ax</tex> <tex dpi="130">\bmod</tex> <tex dpi="130">2^b)</tex> <tex dpi="130">div</tex> <tex dpi="130">2^{b - s}</tex>. | ||
| − | + | Данный алгоритм базируется на [[#lemma1|лемме №1]]. | |
| − | + | Взяв <tex dpi="130">s = 2 \log n</tex>, получаем хеш-функцию <tex dpi="130">h_{a}</tex>, которая захеширует <tex dpi="130">n</tex> чисел из <tex dpi="130">U</tex> в таблицу размера <tex dpi="130">O(n^2)</tex> без коллизий. Очевидно, что <tex dpi="130">h_{a}(x)</tex> может быть посчитана для любого <tex dpi="130">x</tex> за константное время. Если упаковать несколько чисел в один контейнер так, что они разделены несколькими битами нулей, то можно применить <tex dpi="130">h_{a}</tex> ко всему контейнеру, и в результате все хеш-значения для всех чисел в контейнере будут посчитаны. Заметим, что это возможно только потому, что в вычисление хеш-значения вовлечены только (<tex dpi="130">\bmod</tex> <tex dpi="130">2^b</tex>) и (<tex dpi="130">div</tex> <tex dpi="130">2^{b - s}</tex>). | |
| − | + | Такая хеш-функция может быть найдена за <tex dpi="130">O(n^3)</tex>. | |
| + | Следует отметить, что, несмотря на размер таблицы <tex dpi="130">O(n^2)</tex>, потребность в памяти не превышает <tex dpi="130">O(n)</tex>, потому что хеширование используется только для уменьшения количества бит в числе. | ||
| − | + | ==Сортировка по ключу== | |
| + | Предположим, что <tex dpi="130">n</tex> чисел должны быть отсортированы, и в каждом <tex dpi="130">\log m</tex> бит. Будем считать, что в каждом числе есть <tex dpi="130">h</tex> сегментов, в каждом из которых <tex dpi="130">\log</tex> <tex dpi="150">\frac{m}{h}</tex> бит. Теперь применяем хеширование ко всем сегментам и получаем <tex dpi="130">2h \log n</tex> бит хешированных значений для каждого числа. После сортировки на хешированных значениях для всех начальных чисел начальная задача по сортировке <tex dpi="130">n</tex> чисел по <tex dpi="130">\log m</tex> бит в каждом стала задачей по сортировке <tex dpi="130">n</tex> чисел по <tex dpi="130">\log</tex> <tex dpi="150">\frac{m}{h}</tex> бит в каждом. | ||
| − | + | Также рассмотрим проблему последующего разделения. Пусть <tex dpi="130">a_{1}</tex>, <tex dpi="130">a_{2}</tex>, <tex dpi="130">\ldots</tex>, <tex dpi="130">a_{p}</tex> {{---}} <tex dpi="130">p</tex> чисел и <tex dpi="130">S</tex> {{---}} множество чисeл. Необходимо разделить <tex dpi="130">S</tex> в <tex dpi="130">p + 1</tex> наборов, таких, что: <tex dpi="130">S_{0} < a_{1} < S_{1} < a_{2} < \ldots < a_{p} < S_{p}</tex>. Так как используется '''сортировка по ключу''' (англ. ''signature sorting'') то перед тем, как делать вышеописанное разделение, необходимо поделить биты в <tex dpi="130">a_{i}</tex> на <tex dpi="130">h</tex> сегментов и взять некоторые из них. Так же делим биты для каждого числа из <tex dpi="130">S</tex> и оставляем только один в каждом числе. По существу, для каждого <tex dpi="130">a_{i}</tex> берутся все <tex dpi="130">h</tex> сегментов. Если соответствующие сегменты <tex dpi="130">a_{i}</tex> и <tex dpi="130">a_{j}</tex> совпадают, то нам понадобится только один. Сегмент, который берется для числа в <tex dpi="130">S</tex> это сегмент, который выделяется из <tex dpi="130">a_{i}</tex>. Таким образом, начальная задача о разделении <tex dpi="130">n</tex> чисел по <tex dpi="130">\log m</tex> бит преобразуется в несколько задач на разделение с числами по <tex dpi="150">\frac{\log m}{h}</tex> бит. | |
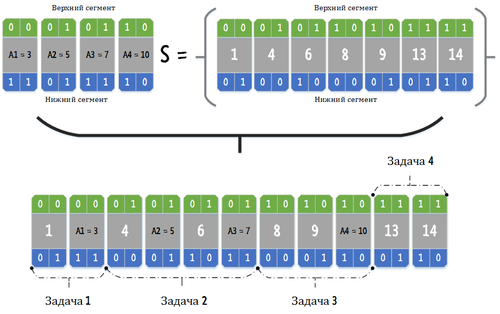
| − | + | '''Пример''': | |
| + | [[Файл:Han-example.png|500px|thumb]] | ||
| + | <tex dpi="130">a_{1} = 3, a_{2} = 5, a_{3} = 7, a_{4} = 10, S = \{1, 4, 6, 8, 9, 13, 14\}</tex>. | ||
| − | + | Делим числа на два сегмента. Для <tex dpi="130">a_{1}</tex> получим верхний сегмент <tex dpi="130">0</tex>, нижний <tex dpi="130">3</tex>; <tex dpi="130">a_{2}</tex> {{---}} верхний <tex dpi="130">1</tex>, нижний <tex dpi="130">1</tex>; <tex dpi="130">a_{3}</tex> {{---}} верхний <tex dpi="130">1</tex>, нижний <tex dpi="130">3</tex>; <tex dpi="130">a_{4}</tex> {{---}} верхний <tex dpi="130">2</tex>, нижний <tex dpi="130">2</tex>. Для элементов из S получим: для <tex dpi="130">1</tex> нижний <tex dpi="130">1</tex>, так как он выделяется из нижнего сегмента <tex dpi="130">a_{1}</tex>; для <tex dpi="130">4</tex> нижний <tex dpi="130">0</tex>; для <tex dpi="130">8</tex> нижний <tex dpi="130">0</tex>; для <tex dpi="130">9</tex> нижний <tex dpi="130">1</tex>; для <tex dpi="130">13</tex> верхний <tex dpi="130">3</tex>; для <tex dpi="130">14</tex> верхний <tex dpi="130">3</tex>. Теперь все верхние сегменты, нижние сегменты <tex dpi="130">1</tex> и <tex dpi="130">3</tex>, нижние сегменты <tex dpi="130">4, 5, 6, 7,</tex> нижние сегменты <tex dpi="130">8, 9, 10</tex> формируют <tex dpi="130">4</tex> новые задачи на разделение. | |
| − | |||
| − | + | Использование '''сортировки по ключу''' в данном алгоритме: | |
| − | == | + | Есть набор <tex dpi="130">T</tex> из <tex dpi="130">p</tex> чисел, которые отсортированы как <tex dpi="130">a_{1}, a_{2}, \ldots, a_{p}</tex>. Используем числа в <tex dpi="130">T</tex> для разделения набора <tex dpi="130">S</tex> из <tex dpi="130">q</tex> чисел <tex dpi="130">b_{1}, b_{2}, \ldots, b_{q}</tex> в <tex dpi="130">p + 1</tex> наборов <tex dpi="130">S_{0}, S_{1}, \ldots, S_{p}</tex>. Пусть <tex dpi="150">h = \frac{\log n}{c \log p}</tex> для константы <tex dpi="130">c > 1</tex>. (<tex dpi="150">\frac{h}{\log\log n \log p}</tex>)-битные числа могут храниться в одном контейнере, содержащим <tex dpi="150">\frac{\log n}{c \log\log n}</tex> бит. Сначала рассматриваем биты в каждом <tex dpi="130">a_{i}</tex> и каждом <tex dpi="130">b_{i}</tex> как сегменты одинаковой длины <tex dpi="150">\frac{h} {\log\log n}</tex>. Рассматриваем сегменты как числа. Чтобы получить неконсервативное преимущество для сортировки, числа в этих контейнерах (<tex dpi="130">a_{i}</tex>-ом и <tex dpi="130">b_{i}</tex>-ом) хешируются, и получается <tex dpi="150">\frac{h}{\log\log n}</tex> хешированных значений в одном контейнере. При вычислении хеш-значений сегменты не влияют друг на друга, можно даже отделить четные и нечетные сегменты в два контейнера. Не умаляя общности считаем, что хеш-значения считаются за константное время. Затем, посчитав значения, два контейнера объединяем в один. Пусть <tex dpi="130">a'_{i}</tex> {{---}} хеш-контейнер для <tex dpi="130">a_{i}</tex>, аналогично <tex dpi="130">b'_{i}</tex>. В сумме хеш-значения имеют <tex dpi="150">\frac{2 \log n}{c \log\log n}</tex> бит, хотя эти значения разделены на сегменты по <tex dpi="150">\frac{h}{ \log\log n}</tex> бит в каждом контейнере. Между сегментами получаются пустоты, которые забиваются нулями. Сначала упаковываются все сегменты в <tex dpi="150">\frac{2 \log n}{c \log\log n}</tex> бит. Потом рассматривается каждый хеш-контейнер как число, и эти хеш-контейнеры сортируются за линейное время (сортировка будет рассмотрена чуть позже). После этой сортировки биты в <tex dpi="130">a_{i}</tex> и <tex dpi="130">b_{i}</tex> разрезаны на <tex dpi="150">\frac{\log\log n}{h}</tex> сегментов. Таким образом, получилось дополнительное мультипликативное преимущество (англ. ''additional multiplicative advantage'') в <tex dpi="150">\frac{h} {\log\log n}</tex>. |
| − | |||
| + | После того, как вышеописанный процесс повторится <tex dpi="130">g</tex> раз, получится неконсервативное преимущество в <tex dpi="150">(\frac{h} {\log\log n})^g</tex> раз, в то время как потрачено только <tex dpi="130">O(gqt)</tex> времени, так как каждое многократное деление происходит за линейное время <tex dpi="130">O(qt)</tex>. | ||
| − | |||
| − | + | Хеш-функция, которая используется, находится следующим образом. Будут хешироватся сегменты, <tex dpi="150">\frac{\log\log n}{h}</tex>-ые, <tex dpi="150">(\frac{\log\log n}{h})^2</tex>-ые, <tex dpi="130">\ldots</tex> по счету в числе. Хеш-функцию для <tex dpi="150">(\frac{\log\log n}{h})^t</tex>-ых по счету сегментов, получаем нарезанием всех <tex dpi="130">p</tex> чисел на <tex dpi="150">(\frac{\log\log n}{h})^t</tex> сегментов. Рассматривая каждый сегмент как число, получаем <tex dpi="150">p(\frac{\log\log n}{h})^t</tex> чисел. Затем получаем одну хеш-функцию для этих чисел. Так как <tex dpi="130">t < \log n</tex>, то получится не более <tex dpi="130">\log n</tex> хеш-функций. | |
| − | + | Рассмотрим сортировку за линейное время, о которой было упомянуто ранее. Предполагается, что хешированные значения для каждого контейнера упакованы в <tex dpi="150">\frac{2 \log n}{c \log\log n}</tex> бит. Есть <tex dpi="130">t</tex> наборов, в каждом из которых <tex dpi="130">q + p</tex> хешированных контейнеров по <tex dpi="150">\frac{2 \log n}{c \log\log n}</tex> бит в каждом. Эти контейнеры должны быть отсортированы в каждом наборе. Комбинируя все хеш-контейнеры в один pool, сортируем следующим образом. | |
| − | + | Операция '''сортировки за линейное время''' (англ. ''Linear-Time-Sort'') | |
| − | + | Входные данные: <tex dpi="150">r \geqslant n^{\frac{2}{5}}</tex> чисел <tex dpi="130">d_{i}</tex>, <tex dpi="130">d_{i}.value</tex> — значение числа <tex dpi="130">d_{i}</tex>, в котором <tex dpi="150">\frac{2 \log n}{c \log\log n}</tex> бит, <tex dpi="130">d_{i}.set</tex> — набор, в котором находится <tex dpi="130">d_{i}</tex>. Следует отметить, что всего есть <tex dpi="130">t</tex> наборов. | |
| − | + | # Сортируем все <tex dpi="130">d_{i}</tex> по <tex dpi="130">d_{i}.value</tex>, используя bucket sort. Пусть все отсортированные числа в <tex dpi="130">A[1..r]</tex>. Этот шаг занимает линейное время, так как сортируется не менее <tex dpi="150">n^{\frac{2}{5}}</tex> чисел. | |
| − | + | # Помещаем все <tex dpi="130">A[j]</tex> в <tex dpi="130">A[j].set</tex>. | |
| + | ==Сортировка с использованием O(n log log n) времени и памяти== | ||
| + | Для сортировки <tex dpi="130">n</tex> целых чисел в диапазоне <tex dpi="130">\{0, 1, \ldots, m - 1\}</tex> предполагается, что в нашем консервативном алгоритме используется контейнер длины <tex dpi="130">O(\log (m + n))</tex>. Далее везде считается, что все числа упакованы в контейнеры одинаковой длины. | ||
| − | |||
| + | Берем <tex dpi="130">1/e = 5</tex> для ЭП-дерева Андерссона. Следовательно, у корня будет <tex dpi="150">n^{\frac{1}{5}}</tex> детей, и каждое ЭП-дерево в каждом ребенке будет иметь <tex dpi="150">n^{\frac{4}{5}}</tex> листьев. В отличие от оригинального дерева, за раз вставляется не один элемент, а <tex dpi="130">d^2</tex>, где <tex dpi="130">d</tex> — количество детей узла дерева, в котором числа должны спуститься вниз. Алгоритм полностью опускает все <tex dpi="130">d^2</tex> чисел на один уровень. В корне опускаются <tex dpi="150">n^{\frac{2}{5}}</tex> чисел на следующий уровень. После того, как все числа опустились на следующий уровень, они успешно разделились на <tex dpi="130">t_{1} = n^{1/5}</tex> наборов <tex dpi="130">S_{1}, S_{2}, \ldots, S_{t_{1}}</tex>, в каждом из которых <tex dpi="150">n^{\frac{4}{5}}</tex> чисел и <tex dpi="130">S_{i} < S_{j}, i < j</tex>. Затем, берутся <tex dpi="150">n^{\frac{8}{25}}</tex> чисел из <tex dpi="130">S_{i}</tex> и опускаются на следующий уровень ЭП-дерева. Это повторяется, пока все числа не опустятся на следующий уровень. На этом шаге числа разделены на <tex dpi="150">t_{2} = n^{\frac{1}{5}}n^{\frac{4}{25}} = n^{\frac{9}{25}}</tex> наборов <tex dpi="130">T_{1}, T_{2}, \ldots, T_{t_{2}}</tex>, аналогичных наборам <tex dpi="130">S_{i}</tex>, в каждом из которых <tex dpi="150">n^{\frac{16}{25}}</tex> чисел. Теперь числа опускаются дальше в ЭП-дереве. | ||
| − | + | Нетрудно заметить, что перебалансирока занимает <tex dpi="130">O(n \log\log n)</tex> времени с <tex dpi="130">O(n)</tex> времени на уровень, аналогично стандартному ЭП-дереву Андерссона. | |
| − | |||
| − | + | Нам следует нумеровать уровни ЭП-дерева с корня, начиная с нуля. Рассмотрим спуск вниз на уровне <tex dpi="130">s</tex>. Имеется <tex dpi="150">t = n^{1 - (\frac{4}{5})^S}</tex> наборов по <tex dpi="150">n^{(\frac{4}{5})^S}</tex> чисел в каждом. Так как каждый узел на данном уровне имеет <tex dpi="150">p = n^{\frac{1}{5} \cdot (\frac{4}{5})^S}</tex> детей, то на <tex dpi="130">s + 1</tex> уровень опускаются <tex dpi="150">q = n^{\frac{2}{5} \cdot (\frac{4}{5})^S}</tex> чисел для каждого набора, или всего <tex dpi="150">qt \geqslant n^{\frac{2}{5}}</tex> чисел для всех наборов за один раз. | |
| − | + | Спуск вниз можно рассматривать как сортировку <tex dpi="130">q</tex> чисел в каждом наборе вместе с <tex dpi="130">p</tex> числами <tex dpi="130">a_{1}, a_{2}, \ldots, a_{p}</tex> из ЭП-дерева, так, что эти <tex dpi="130">q</tex> чисел разделены в <tex dpi="130">p + 1</tex> наборов <tex dpi="130">S_{0}, S_{1}, \ldots, S_{p}</tex> таких, что <tex dpi="130">S_{0} < a_{1} < \ldots < a_{p} < S_{p}</tex>. | |
| − | |||
| − | + | Так как <tex dpi="130">q</tex> чисел не надо полностью сортировать и <tex dpi="130">q = p^2</tex>, то можно использовать [[#lemma6|лемму №6]] для сортировки. Для этого необходимо неконсервативное преимущество, которое получается с помощью [[Сортировка Хана#Signature sorting|signature sorting]]. Для этого используется линейная техника многократного деления (англ. ''multi-dividing technique''). | |
| − | + | После <tex dpi="130">g</tex> сокращений бит в [[Сортировка Хана#Signature sorting|signature sorting]] получаем неконсервативное преимущество в <tex dpi="150">(\frac{h}{ \log\log n})^g</tex>. Мы не волнуемся об этих сокращениях до конца потому, что после получения неконсервативного преимущества мы можем переключиться на [[#lemma6|лемму №6]] для завершения разделения <tex dpi="130">q</tex> чисел с помощью <tex dpi="130">p</tex> чисел на наборы. Заметим, что по природе битового сокращения начальная задача разделения для каждого набора перешла в <tex dpi="130">w</tex> подзадач разделения на <tex dpi="130">w</tex> поднаборов для какого-то числа <tex dpi="130">w</tex>. | |
| − | + | Теперь для каждого набора все его поднаборы в подзадачах собираются в один набор. Затем, используя [[#lemma6|лемму №6]], делается разделение. Так как получено неконсервативное преимущество в <tex dpi="150">(\frac{h}{\log\log n})^g</tex> и работа происходит на уровнях не ниже, чем <tex dpi="130">2 \log\log\log n</tex>, то алгоритм занимает <tex dpi="150">O(\frac{qt \log\log n}{g(\log h - \log\log\log n) - \log\log\log n}) = O(\log\log n)</tex> времени. | |
| − | + | В итоге разделились <tex dpi="130">q</tex> чисел <tex dpi="130">p</tex> числами в каждый набор. То есть получилось, что <tex dpi="130">S_{0} < e_{1} < S_{1} < \ldots < e_{p} < S_{p}</tex>, где <tex dpi="130">e_{i}</tex> {{---}} сегмент <tex dpi="130">a_{i}</tex>, полученный с помощью битового сокращения. Такое разделение получилось комбинированием всех поднаборов в подзадачах. Предполагаем, что числа хранятся в массиве <tex dpi="130">B</tex> так, что числа в <tex dpi="130">S_{i}</tex> предшествуют числам в <tex dpi="130">S_{j}</tex> если <tex dpi="130">i < j</tex> и <tex dpi="130">e_{i}</tex> хранится после <tex dpi="130">S_{i - 1}</tex>, но до <tex dpi="130">S_{i}</tex>. | |
| − | |||
| − | + | Пусть <tex dpi="130">B[i]</tex> находится в поднаборе <tex dpi="130">B[i].subset</tex>. Чтобы позволить разделению выполниться, для каждого поднабора помещаем все <tex dpi="130">B[j]</tex> в <tex dpi="130">B[j].subset</tex>. | |
| − | |||
| + | На это потребуется линейное время и место. | ||
| + | Теперь рассмотрим проблему упаковки, которая решается следующим образом. Считается, что число бит в контейнере <tex dpi="130">\log m \geqslant \log\log\log n</tex>, потому что в противном случае можно использовать radix sort для сортировки чисел. У контейнера есть <tex dpi="150">\frac{h}{\log\log n}</tex> хешированных значений (сегментов) в себе на уровне <tex dpi="130">\log h</tex> в ЭП-дереве. Полное число хешированных бит в контейнере равно <tex dpi="130">(2 \log n)(c \log\log n)</tex> бит. Хешированные биты в контейнере выглядят как <tex dpi="130">0^{i}t_{1}0^{i}t_{2} \ldots t</tex><tex dpi="150">_{\frac{h}{\log\log n}}</tex>, где <tex dpi="130">t_{k}</tex>-ые — хешированные биты, а нули {{---}} это просто нули. Сначала упаковываем <tex dpi="130">\log\log n</tex> контейнеров в один и получаем <tex dpi="130">w_{1} = 0^{j}t_{1, 1}t_{2, 1} \ldots t_{\log\log n, 1}0^{j}t_{1, 2} \ldots t_{\log\log n,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex>, где <tex dpi="130">t_{i, k}</tex>: элемент с номером <tex dpi="130">k = 1, 2, \ldots, </tex><tex dpi="150">\frac{h}{\log\log n}</tex> из <tex dpi="130">i</tex>-ого контейнера. Используем <tex dpi="130">O(\log\log n)</tex> шагов, чтобы упаковать <tex dpi="130">w_{1}</tex> в <tex dpi="130">w_{2} = 0</tex><tex dpi="150">^{\frac{jh}{\log\log n}}</tex><tex dpi="130">t_{1, 1}t_{2, 1} \ldots t_{\log\log n, 1}t_{1, 2}t_{2, 2} \ldots t_{1,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex><tex dpi="130">t_{2,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex><tex dpi="130">\ldots t_{\log\log n,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex>. Теперь упакованные хеш-биты занимают <tex dpi="130">2 \log</tex><tex dpi="150">\frac{n}{c}</tex> бит. Используем <tex dpi="130">O(\log\log n)</tex> времени чтобы распаковать <tex dpi="130">w_{2}</tex> в <tex dpi="130">\log\log n</tex> контейнеров <tex dpi="130">w_{3, k} = 0</tex><tex dpi="150">^{\frac{jh}{\log\log n}}</tex><tex dpi="130">0^{r}t_{k, 1}0^{r}t_{k, 2} \ldots t_{k,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex> <tex dpi="130">k = 1, 2, \ldots, \log\log n</tex>. Затем, используя <tex dpi="130">O(\log\log n)</tex> времени, упаковываем эти <tex dpi="130">\log\log n</tex> контейнеров в один <tex dpi="130">w_{4} = 0^{r}t_{1, 1}0^{r}t_{1, 2} \ldots t_{1,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex><tex dpi="130">0^{r}t_{2, 1} \ldots t_{\log\log n,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex>. Затем, используя <tex dpi="130">O(\log\log n)</tex> шагов, упаковываем <tex dpi="130">w_{4}</tex> в <tex dpi="130">w_{5} = 0^{s}t_{1, 1}t_{1, 2} \ldots t_{1,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex><tex dpi="130">t_{2, 1}t_{2, 2} \ldots t_{\log\log n,}</tex><tex dpi="150">_{ \frac{h}{\log\log n}}</tex>. В итоге используется <tex dpi="130">O(\log\log n)</tex> времени для упаковки <tex dpi="130">\log\log n</tex> контейнеров. Считаем, что время, потраченное на один контейнер — константа. | ||
| + | ==См. также== | ||
| + | * [[Сортировка подсчетом]] | ||
| + | * [[Цифровая сортировка]] | ||
| − | == | + | ==Источники информации== |
| − | + | * [http://www.sciencedirect.com/science/article/pii/S019667740300155X Deterministic Sorting in O(n log log n) Time and Linear Space. Yijie Han.] | |
| − | + | * А. Андерссон. Fast deterministic sorting and searching in linear space. Proc. 1996 IEEE Symp. on Foundations of Computer Science. 135-141(1996) | |
| + | * [http://dl.acm.org/citation.cfm?id=1236460 A. Andersson, M. Thorup. Dynamic ordered sets with exponential search trees.] | ||
| + | * [[wikipedia:en:Integer_sorting|Wikipedia {{---}} Integer sorting]] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
| − | [[Категория: | + | [[Категория: Сортировка]] |
Версия 00:14, 8 июня 2015
Сортировка Хана (англ. Hansort) — сложный алгоритм сортировки целых чисел со сложностью , где — количество элементов для сортировки.
Данная статья писалась на основе брошюры Хана (англ. Yijie Han), посвященной этой сортировке.
Содержание
Описание
Алгоритм построен на основе экспоненциального поискового дерева Андерсона (англ. Andersson's exponential search tree). Сортировка происходит за счет вставки целых чисел в экспоненциальное поисковое дерево (далее — ЭП-дерево).
Экспоненциальное поисковое дерево Андерсона
| Определение: |
| ЭП-дерево — это дерево поиска, в котором все ключи хранятся в листьях этого дерева и количество детей у каждого узла уменьшается экспоненциально от глубины узла. |
Структура ЭП-дерева:
1) Корень имеет сыновей . Все сыновья являются ЭП-деревьями.
2) Каждое поддерево корня имеет сыновей.
В этом дереве уровней. При нарушении баланса дерева необходимо балансирование, которое требует времени при вставленных целых числах. Такое время достигается за счет вставки чисел группами, а не поодиночке, как изначально предлагал Андерссон.
Определения
| Определение: |
| Контейнер — объект, в которым хранятся наши данные. Например: 32-битные и 64-битные числа, массивы, вектора. |
| Определение: |
| Алгоритм, сортирующий целых чисел из множества , называется консервативным, если длина контейнера (число бит в контейнере) равна . Если длина больше, то алгоритм неконсервативный. |
| Определение: |
| Если сортируются целые числа из множества с длиной контейнера с , тогда сортировка происходит с неконсервативным преимуществом . |
| Определение: |
| Для множества определим
Набор если |
| Определение: |
| Предположим, есть набор из чисел, которые уже отсортированы как и набор из чисел . Тогда разделением чисел числами называется набор , где . |
Леммы
| Лемма (№ 1): |
Даны целые числа , и является подмножеством множества , содержащим элементов, и . Функция , принадлежащая , может быть выбрана за время так, что количество коллизий . |
| Лемма (№ 2): |
Выбор -ого наибольшего числа среди чисел, упакованных в контейнеров, может быть сделан за время и с использованием памяти. В том числе, так может быть найдена медиана. |
| Доказательство: |
| Так как возможно делать попарное сравнение чисел в одном контейнере с числами в другом и извлекать большие числа из одного контейнера и меньшие из другого за константное время, возможно упаковать медианы из первого, второго, , -ого чисел из 5 контейнеров в один контейнер за константное время. Таким образом, набор из медиан теперь содержится в контейнерах. Рекурсивно находим медиану в . Используя , уберем хотя бы чисел среди . Затем упакуем оставшиеся из контейнеров в контейнеров и затем продолжим рекурсию. |
| Лемма (№ 3): |
Если целых чисел, в сумме использующих бит, упакованы в один контейнер, тогда чисел в контейнерах могут быть отсортированы за время с использованием памяти. |
| Доказательство: |
|
Так как используется только бит в каждом контейнере для хранения чисел, используем bucket sort, чтобы отсортировать все контейнеры, представляя каждый как число, что занимает времени и памяти. Так как используется бит на контейнер, понадобится шаблонов для всех контейнеров. Затем поместим контейнеров с одинаковым шаблоном в одну группу. Для каждого шаблона останется не более контейнеров, которые не смогут образовать группу. Поэтому не более контейнеров не смогут сформировать группу. Для каждой группы помещаем -е число во всех контейнерах в один. Таким образом берутся -целых векторов и получаются -целых векторов, где -ый вектор содержит -ое число из входящего вектора. Эта транспозиция может быть сделана за время , с использованием памяти. Для всех групп это занимает время , с использованием памяти. Для контейнеров вне групп (которых штук) разбираем и собираем заново контейнеры. На это потребуется не более времени и памяти. После всего этого используем карманную сортировку вновь для сортировки контейнеров. Таким образом, все числа отсортированы.
|
| Лемма (№ 4): |
Примем, что каждый контейнер содержит бит, и чисел, в каждом из которых бит, упакованы в один контейнер. Если каждое число имеет маркер, содержащий бит, и маркеров упакованы в один контейнер таким же образом, что и числа, тогда чисел в контейнерах могут быть отсортированы по их маркерам за время с использованием памяти.
(*): если число упаковано как -ое число в -ом контейнере для чисел, тогда маркер для упакован как -ый маркер в -ом контейнере для маркеров. |
| Доказательство: |
| Контейнеры для маркеров могут быть отсортированы с помощью bucket sort потому, что каждый контейнер использует бит. Сортировка сгруппирует контейнеры для чисел как в лемме №3. Перемещаем каждую группу контейнеров для чисел. |
| Лемма (№ 5): |
Предположим, что каждый контейнер содержит бит, что чисел, в каждом из которых бит, упакованы в один контейнер, что каждое число имеет маркер, содержащий бит, и что маркеров упакованы в один контейнер тем же образом что и числа. Тогда чисел в контейнерах могут быть отсортированы по своим маркерам за время с использованием памяти. |
| Доказательство: |
|
Заметим, что несмотря на то, что длина контейнера бит, всего бит используется для хранения упакованных чисел. Так же как в лемме №3 и лемме №4 сортируем контейнеры упакованных маркеров с помощью bucket sort. Для того, чтобы перемещать контейнеры чисел, помещаем вместо контейнеров чисел в одну группу. Для транспозиции чисел в группе, содержащей контейнеров, упаковываем контейнеров в , упаковывая контейнеров в один. Далее делаем транспозицию над контейнерами. Таким образом перемещение занимает всего времени для каждой группы и времени для всех чисел. После завершения транспозиции, распаковываем контейнеров в контейнеров.
|
| Лемма (№ 6): |
целых чисел можно отсортировать в наборов , , , таким образом, что в каждом наборе чисел и при , за время и место с неконсервативным преимуществом . |
| Доказательство: |
|
Алгоритм сортировки целых чисел в наборов, представленный ниже, является доказательством данной леммы. Постановка задачи и решение некоторых проблем:
Стоит отметить, что процесс помещения нестабилен, т.к. основан на алгоритме из леммы №5.
Рассмотрим число , которое является -ым в наборе . Рассмотрим блок (назовем его ), который является -ым м.ч. в . Когда используется вышеописанный метод перемещения нескольких следующих блоков (назовем это ) в , просто перемещен на позицию в наборе , но не обязательно на позицию (где расположен ). Если значение блока одинаково для всех чисел в , то это не создаст проблемы потому, что блок одинаков вне зависимости от того в какое место в помещен . Иначе у нас возникает проблема дальнейшей сортировки. Поэтому поступаем следующим образом: На каждой стадии числа в одном наборе работают на общем блоке, который назовем "текущий блок набора". Блоки, которые предшествуют текущему блоку содержат важные биты и идентичны для всех чисел в наборе. Когда помещаем больше бит в набор, последующие блоки помещаются в набор вместе с текущим блоком. Так вот, в вышеописанном процессе помещения предполагается, что самый значимый блок среди блоков — это текущий блок. Таким образом, после того, как эти блоков помещены в набор, изначальный текущий блок удаляется, потому что известно, что эти блоков перемещены в правильный набор, и нам не важно где находился начальный текущий блок. Тот текущий блок находится в перемещенных блоках.
Алгоритм сортировкиAlgorithm , , , , , ) — это неконсервативное преимущество равное , -ые это входящие целые числа в наборе, которые надо отсортировать, это уровень рекурсии.
Algorithm IterateSort Call , , , , , ); от 1 до 5
|
Уменьшение числа бит в числах
Один из способов ускорить сортировку — уменьшить число бит в числе. Один из способов уменьшить число бит в числе — использовать деление пополам (эту идею впервые подал van Emde Boas). Деление пополам заключается в том, что количество оставшихся бит в числе уменьшается в 2 раза. Это быстрый способ, требующий памяти. Для своего дерева Андерссон использует хеширование, что позволяет сократить количество памяти до . Для того чтобы еще ускорить алгоритм, необходимо упаковать несколько чисел в один контейнер, чтобы затем за константное количество шагов произвести хеширование для всех чисел, хранимых в контейнере. Для этого используется хеш-функция для хеширования чисел в таблицу размера за константное время без коллизий. Для этого используется модифицированная хеш-функция авторства: Dierzfelbinger и Raman.
Алгоритм: Пусть целое число и пусть . Класс хеш-функций из в определен как и для всех из : .
Данный алгоритм базируется на лемме №1.
Взяв , получаем хеш-функцию , которая захеширует чисел из в таблицу размера без коллизий. Очевидно, что может быть посчитана для любого за константное время. Если упаковать несколько чисел в один контейнер так, что они разделены несколькими битами нулей, то можно применить ко всему контейнеру, и в результате все хеш-значения для всех чисел в контейнере будут посчитаны. Заметим, что это возможно только потому, что в вычисление хеш-значения вовлечены только ( ) и ( ).
Такая хеш-функция может быть найдена за .
Следует отметить, что, несмотря на размер таблицы , потребность в памяти не превышает , потому что хеширование используется только для уменьшения количества бит в числе.
Сортировка по ключу
Предположим, что чисел должны быть отсортированы, и в каждом бит. Будем считать, что в каждом числе есть сегментов, в каждом из которых бит. Теперь применяем хеширование ко всем сегментам и получаем бит хешированных значений для каждого числа. После сортировки на хешированных значениях для всех начальных чисел начальная задача по сортировке чисел по бит в каждом стала задачей по сортировке чисел по бит в каждом.
Также рассмотрим проблему последующего разделения. Пусть , , , — чисел и — множество чисeл. Необходимо разделить в наборов, таких, что: . Так как используется сортировка по ключу (англ. signature sorting) то перед тем, как делать вышеописанное разделение, необходимо поделить биты в на сегментов и взять некоторые из них. Так же делим биты для каждого числа из и оставляем только один в каждом числе. По существу, для каждого берутся все сегментов. Если соответствующие сегменты и совпадают, то нам понадобится только один. Сегмент, который берется для числа в это сегмент, который выделяется из . Таким образом, начальная задача о разделении чисел по бит преобразуется в несколько задач на разделение с числами по бит.
Пример:
.
Делим числа на два сегмента. Для получим верхний сегмент , нижний ; — верхний , нижний ; — верхний , нижний ; — верхний , нижний . Для элементов из S получим: для нижний , так как он выделяется из нижнего сегмента ; для нижний ; для нижний ; для нижний ; для верхний ; для верхний . Теперь все верхние сегменты, нижние сегменты и , нижние сегменты нижние сегменты формируют новые задачи на разделение.
Использование сортировки по ключу в данном алгоритме:
Есть набор из чисел, которые отсортированы как . Используем числа в для разделения набора из чисел в наборов . Пусть для константы . ()-битные числа могут храниться в одном контейнере, содержащим бит. Сначала рассматриваем биты в каждом и каждом как сегменты одинаковой длины . Рассматриваем сегменты как числа. Чтобы получить неконсервативное преимущество для сортировки, числа в этих контейнерах (-ом и -ом) хешируются, и получается хешированных значений в одном контейнере. При вычислении хеш-значений сегменты не влияют друг на друга, можно даже отделить четные и нечетные сегменты в два контейнера. Не умаляя общности считаем, что хеш-значения считаются за константное время. Затем, посчитав значения, два контейнера объединяем в один. Пусть — хеш-контейнер для , аналогично . В сумме хеш-значения имеют бит, хотя эти значения разделены на сегменты по бит в каждом контейнере. Между сегментами получаются пустоты, которые забиваются нулями. Сначала упаковываются все сегменты в бит. Потом рассматривается каждый хеш-контейнер как число, и эти хеш-контейнеры сортируются за линейное время (сортировка будет рассмотрена чуть позже). После этой сортировки биты в и разрезаны на сегментов. Таким образом, получилось дополнительное мультипликативное преимущество (англ. additional multiplicative advantage) в .
После того, как вышеописанный процесс повторится раз, получится неконсервативное преимущество в раз, в то время как потрачено только времени, так как каждое многократное деление происходит за линейное время .
Хеш-функция, которая используется, находится следующим образом. Будут хешироватся сегменты, -ые, -ые, по счету в числе. Хеш-функцию для -ых по счету сегментов, получаем нарезанием всех чисел на сегментов. Рассматривая каждый сегмент как число, получаем чисел. Затем получаем одну хеш-функцию для этих чисел. Так как , то получится не более хеш-функций.
Рассмотрим сортировку за линейное время, о которой было упомянуто ранее. Предполагается, что хешированные значения для каждого контейнера упакованы в бит. Есть наборов, в каждом из которых хешированных контейнеров по бит в каждом. Эти контейнеры должны быть отсортированы в каждом наборе. Комбинируя все хеш-контейнеры в один pool, сортируем следующим образом.
Операция сортировки за линейное время (англ. Linear-Time-Sort)
Входные данные: чисел , — значение числа , в котором бит, — набор, в котором находится . Следует отметить, что всего есть наборов.
- Сортируем все по , используя bucket sort. Пусть все отсортированные числа в . Этот шаг занимает линейное время, так как сортируется не менее чисел.
- Помещаем все в .
Сортировка с использованием O(n log log n) времени и памяти
Для сортировки целых чисел в диапазоне предполагается, что в нашем консервативном алгоритме используется контейнер длины . Далее везде считается, что все числа упакованы в контейнеры одинаковой длины.
Берем для ЭП-дерева Андерссона. Следовательно, у корня будет детей, и каждое ЭП-дерево в каждом ребенке будет иметь листьев. В отличие от оригинального дерева, за раз вставляется не один элемент, а , где — количество детей узла дерева, в котором числа должны спуститься вниз. Алгоритм полностью опускает все чисел на один уровень. В корне опускаются чисел на следующий уровень. После того, как все числа опустились на следующий уровень, они успешно разделились на наборов , в каждом из которых чисел и . Затем, берутся чисел из и опускаются на следующий уровень ЭП-дерева. Это повторяется, пока все числа не опустятся на следующий уровень. На этом шаге числа разделены на наборов , аналогичных наборам , в каждом из которых чисел. Теперь числа опускаются дальше в ЭП-дереве.
Нетрудно заметить, что перебалансирока занимает времени с времени на уровень, аналогично стандартному ЭП-дереву Андерссона.
Нам следует нумеровать уровни ЭП-дерева с корня, начиная с нуля. Рассмотрим спуск вниз на уровне . Имеется наборов по чисел в каждом. Так как каждый узел на данном уровне имеет детей, то на уровень опускаются чисел для каждого набора, или всего чисел для всех наборов за один раз.
Спуск вниз можно рассматривать как сортировку чисел в каждом наборе вместе с числами из ЭП-дерева, так, что эти чисел разделены в наборов таких, что .
Так как чисел не надо полностью сортировать и , то можно использовать лемму №6 для сортировки. Для этого необходимо неконсервативное преимущество, которое получается с помощью signature sorting. Для этого используется линейная техника многократного деления (англ. multi-dividing technique).
После сокращений бит в signature sorting получаем неконсервативное преимущество в . Мы не волнуемся об этих сокращениях до конца потому, что после получения неконсервативного преимущества мы можем переключиться на лемму №6 для завершения разделения чисел с помощью чисел на наборы. Заметим, что по природе битового сокращения начальная задача разделения для каждого набора перешла в подзадач разделения на поднаборов для какого-то числа .
Теперь для каждого набора все его поднаборы в подзадачах собираются в один набор. Затем, используя лемму №6, делается разделение. Так как получено неконсервативное преимущество в и работа происходит на уровнях не ниже, чем , то алгоритм занимает времени.
В итоге разделились чисел числами в каждый набор. То есть получилось, что , где — сегмент , полученный с помощью битового сокращения. Такое разделение получилось комбинированием всех поднаборов в подзадачах. Предполагаем, что числа хранятся в массиве так, что числа в предшествуют числам в если и хранится после , но до .
Пусть находится в поднаборе . Чтобы позволить разделению выполниться, для каждого поднабора помещаем все в .
На это потребуется линейное время и место.
Теперь рассмотрим проблему упаковки, которая решается следующим образом. Считается, что число бит в контейнере , потому что в противном случае можно использовать radix sort для сортировки чисел. У контейнера есть хешированных значений (сегментов) в себе на уровне в ЭП-дереве. Полное число хешированных бит в контейнере равно бит. Хешированные биты в контейнере выглядят как , где -ые — хешированные биты, а нули — это просто нули. Сначала упаковываем контейнеров в один и получаем , где : элемент с номером из -ого контейнера. Используем шагов, чтобы упаковать в . Теперь упакованные хеш-биты занимают бит. Используем времени чтобы распаковать в контейнеров . Затем, используя времени, упаковываем эти контейнеров в один . Затем, используя шагов, упаковываем в . В итоге используется времени для упаковки контейнеров. Считаем, что время, потраченное на один контейнер — константа.
См. также
Источники информации
- Deterministic Sorting in O(n log log n) Time and Linear Space. Yijie Han.
- А. Андерссон. Fast deterministic sorting and searching in linear space. Proc. 1996 IEEE Symp. on Foundations of Computer Science. 135-141(1996)
- A. Andersson, M. Thorup. Dynamic ordered sets with exponential search trees.
- Wikipedia — Integer sorting