Сортировка подсчётом
Сортировка подсчётом (англ. counting sort) — алгоритм сортировки целых чисел в диапазоне от до некоторой константы или сложных объектов, работающий за линейное время.
Содержание
Сортировка целых чисел
Это простейший вариант алгоритма.
Описание
Исходная последовательность чисел длины , а в конце отсортированная, хранится в массиве . Также используется вспомогательный массив с индексами от до , изначально заполняемый нулями.
- Последовательно пройдём по массиву и запишем в количество чисел, равных .
- Теперь достаточно пройти по массиву и для каждого в массив последовательно записать число раз.
Псевдокод
function simpleCountingSort(A: int[n]):
for number = 0 to k - 1
C[number] = 0
for i = 0 to n - 1
C[A[i]] = C[A[i]] + 1;
pos = 0;
for number = 0 to k - 1
for i = 0 to C[number] - 1
A[pos] = number;
pos = pos + 1;
Сортировка сложных объектов
Сортировка целых чисел за линейное время это хорошо, но недостаточно. Иногда бывает очень желательно применить быстрый алгоритм сортировки подсчетом для упорядочивания набора каких-либо "сложных" данных. Под "сложными объектами" здесь подразумеваются структуры, содержащие в себе несколько полей. Одно из них мы выделим и назовем ключом, сортировка будет идти именно по нему (предполагается, что значения, принимаемые ключом — целые числа в диапазоне от до ).
Мы не сможем использовать здесь в точности тот же алгоритм, что и для сортировки подсчетом обычных целых чисел, потому что в наборе могут быть различные структуры, имеющие одинаковые ключи. Существует два способа справиться с этой проблемой — использовать списки для хранения структур в отсортированном массиве или заранее посчитать количество структур с одинаковыми ключами для каждого значения ключа.
Описание
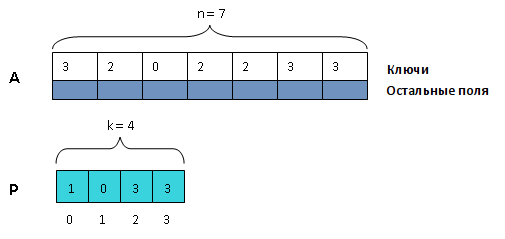
Исходная последовательность из структур хранится в массиве , а отсортированная — в массиве того же размера. Кроме того, используется вспомогательный массив с индексами от до .
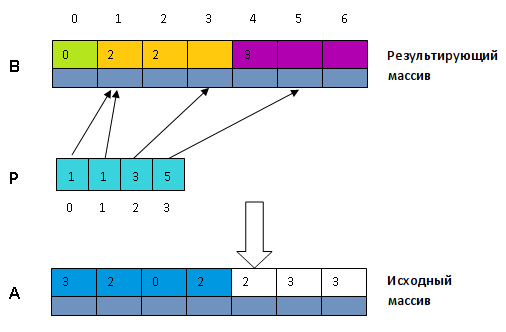
Идея алгоритма состоит в предварительном подсчете количества элементов с различными ключами в исходном массиве и разделении результирующего массива на части соответствующей длины (будем называть их блоками). Затем при повторном проходе исходного массива каждый его элемент копируется в специально отведенный его ключу блок, в первую свободную ячейку. Это осуществляется с помощью массива индексов , в котором хранятся индексы начала блоков для различных ключей. — индекс в результирующем массиве, соответствующий первому элементу блока для ключа .
- Пройдем по исходному массиву и запишем в количество структур, ключ которых равен .
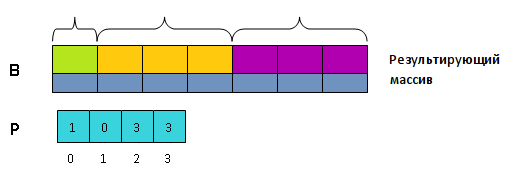
- Мысленно разобьем массив на блоков, длина каждого из которых равна соответственно , , ..., .
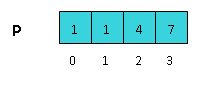
- Теперь массив нам больше не нужен. Превратим его в массив, хранящий в сумму элементов от до старого массива .
- Теперь "сдвинем" массив на элемент вперед: в новом массиве , а для , где — старый массив .
Это можно сделать за один проход по массиву , причем одновременно с предыдущим шагом.
После этого действия в массиве будут хранится индексы массива . указывает на начало блока в , соответствующего ключу .
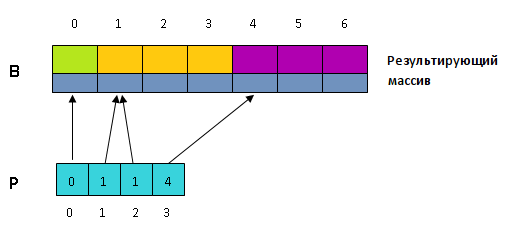
- Произведем саму сортировку. Еще раз пройдем по исходному массиву и для всех будем помещать структуру в массив на место , а затем увеличивать на . Здесь — это ключ структуры, находящейся в массиве на -том месте.
Таким образом после завершения алгоритма в будет содержаться исходная последовательность в отсортированном виде (так как блоки расположены по возрастанию соответствующих ключей).
Стоит также отметить, что эта сортировка является устойчивой, так как два элемента с одинаковыми ключами будут добавлены в том же порядке, в каком просматривались в исходном массиве . Благодаря этому свойству существует цифровая сортировка.
Псевдокод
Здесь и — массивы структур размера , с индексами от до .
— целочисленный массив размера , с индексами от до , где — количество различных ключей.
function complexCountingSort(A: int[n], B: int[n]):
for i = 0 to k - 1
P[i] = 0;
for i = 0 to length[A] - 1
P[A[i].key] = P[A[i].key] + 1;
carry = 0;
for i = 0 to k - 1
temporary = P[i];
P[i] = carry;
carry = carry + temporary;
for i = 0 to length[A] - 1
B[P[A[i].key]] = A[i];
P[A[i].key] = P[A[i].key] + 1;
Здесь шаги 3 и 4 из описания объединены в один цикл. Обратите внимание, что в последнем цикле инструкцией
B[P[A[i].key]] = A[i];
копируется структура целиком, а не только её ключ.
Анализ
В первом алгоритме первые два цикла работают за и , соответственно; двойной цикл за . Алгоритм имеет линейную временную трудоёмкость . Используемая дополнительная память равна .
Второй алгоритм состоит из двух проходов по массиву размера и одного прохода по массиву размера .
Его трудоемкость, таким образом, равна . На практике сортировку подсчетом имеет смысл применять, если , поэтому можно считать время работы алгоритма равным .
Как и в обычной сортировке подсчетом, требуется дополнительной памяти — на хранение массива размера и массива размера .
Алгоритм работает за линейное время, но является псевдополиномиальным.
Поиск диапазона ключей
Если диапазон значений не известен заранее, то его можно найти с помощью линейного поиска минимума и максимума в исходном массиве, что не повлияет на асимптотику алгоритма.
Нужно учитывать, что минимум может быть отрицательным, в то время как в массиве индексы от до . Поэтому при работе с массивом из исходного необходимо вычитать минимум, а при обратной записи в прибавлять его.
Источники информации
- Сортировка подсчетом — Википедия
- Counting sort — Wikipedia
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 224—226.