Статические выпуклые оболочки: Джарвис, Грэхем, Эндрю, Чен, QuickHull
| Конспект готов к прочтению. |
| Определение: |
| Выпуклой оболочкой множества точек называется пересечение всех выпуклых множеств, содержащих все заданные точки. |
Ниже приводятся основные алгоритмы построения выпуклых оболочек статического множества. Используются обозначения: - размер входных данных, - размер оболочки.
Содержание
Алгоритм Джарвиса
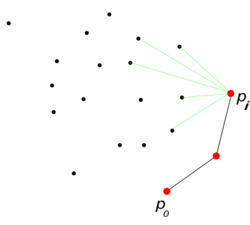
По-другому "Gift wrapping algorithm" (Заворачивание подарка). Он заключается в том, что мы ищем выпуклую оболочку последовательно, против часовой стрелки, начиная с определенной точки.
Описание Алгоритма
- Возьмем точку нашего множества с самой маленькой у-координатой (если таких несколько, берем самую правую из них). Добавляем ее в ответ.
- На каждом следующем шаге для последнего добавленного ищем среди всех недобавленных точек и с максимальным полярным углом относительно (Если углы равны, надо сравнивать по расстоянию). Добавляем в ответ. Если , заканчиваем алгоритм.
Корректность
Точка , очевидно, принадлежит оболочке. На каждом последующем шаге алгоритма мы получаем прямую , по построению которой все точки множества лежат слева от нее. Значит, выпуклая оболочка состоит из -ых и только из них.
Псевдокод
Inplace-реализация алгоритма. - исходное множество,
Jarvis(S)
find i such that S[i] has the lowest y-coordinate and highest x-coordinate
p0 = S[i]
pi = p0
k = 0
do
k++
for i = k..n
if S[i] has lower angle and higher distance than S[k] in relation to pi
swap(S[i], S[k])
pi = S[k]
while pi != p0
return k
Сложность
Добавление каждой точки в ответ занимает времени, всего точек будет , поэтому итоговая сложность . В худшем случае, когда оболочка состоит из всех точек сложность .
Ссылки
Алгоритм Грэхема
Алгоритм заключается в том, что мы ищем точки оболочки последовательно, используя стек.
Описание Алгоритма
- Находим точку нашего множества с самой маленькой у-координатой (если таких несколько, берем самую правую из них), добавляем в ответ.
- Сортируем все остальные точки по полярному углу относительно .
- Добавляем в ответ - самую первую из отсортированных точек.
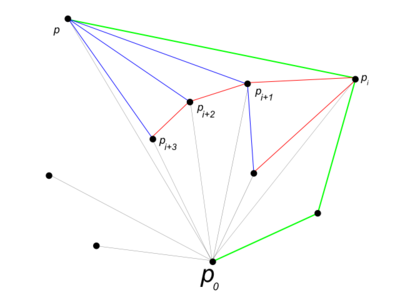
- Берем следующую по счету точку . Пока и две последних точки в текущей оболочке и образуют неправый поворот (вектора и ), удаляем из оболочки .
- Добавляем в оболочку .
- Делаем п.5, пока не закончатся точки.
Корректность
Докажем, что на каждом шаге множество -тых является выпуклой оболочкой всех уже рассмотренных точек. Доказательство проведем по индукции.
- База. Для трех первых точек утверждение, очевидно, выполняется.
- Переход. Пусть для точек оболочки совпадают. Докажем, что и для точек они совпадут.
Рассмотрим истинную оболочку , где - множество всех точек из , видимых из . Так как мы добавляли точки в нашу оболочку против часовой стрелки и так как -тая точка лежит в , то состоит из нескольких подряд идущих последних добавленных в оболочку точек, и именно их мы удаляем на текущем шаге. Поэтому наша оболочка и истинная для точек совпадают.
Тогда по индукции оболочки совпадают и для .
Псевдокод
Inplace-реализация алгоритма. - исходное множество,
Graham(S)
find i such that S[i] has the lowest y-coordinate and highest x-coordinate
swap(S[i], S[1])
sort S[2..n] by angle in relation to S[1]
k = 2
for p = 3..n
while S[k - 1], S[k], S[p] has non-right orientation and k > 1
k--
swap(S[p], S[k + 1])
k++
return k + 1
Сложность
Сортировка точек занимает времени. При обходе каждая точка добавляется в ответ не более одного раза, поэтому сложность этой части - . Суммарное время — .
Ссылки
Алгоритм Эндрю
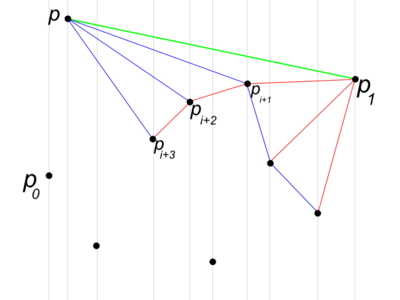
Алгоритм, очень похожий на алгоритм Грехема. Он заключается в том, что мы находим самую левую и самую правую точки, ищем для точек над и под этой прямой выпуклую оболочку Грехемом - для них начальные точки будут лежать на , а сортировка по углу относительно далекой точки аналогична сортировке по координате; после этого объединяем две оболочки в одну.
Описание Алгоритма
- Находим самую левую и самую правую точки множества - и .
- Делим множество на две части: точки над и под прямой.
- Для каждой половины ищем выпуклую оболочку Грехемом с условием, что сортируем не по полярному углу, а по координате.
- Сливаем получившиеся оболочки.
Корректность
См. доказательство алгоритма Грехема.
Псевдокод
Inplace-реализация алгоритма. - исходное множество,
Andrew(S)
sort S[1..n] by x-coordinate backward(than by y backward)
k = 2
for p = 3..n
while S[k - 1], S[k], S[p] has non-right orientation
k--
swap(S[p], S[k + 1])
k++
sort S[k + 1..n] by x-coordinate (than by y)
for p = k + 1..n
while S[k - 1], S[k], S[p] has non-right orientation
k--
swap(S[p], S[k + 1])
return k + 1
Сложность
Сортировка точек занимает времени. При обходе каждая точка добавляется в ответ не более одного раза, поэтому сложность двух обходов - . Суммарное время - . Также можно отметить тот факт, что Эндрю в целом работает быстрее чем Грэхем, так как использует всего поворотов, в то время как Грэхем использует поворотов.
Ссылки
Алгоритм Чена
Является комбинацией двух алгоритмов - Джарвиса и Грехема. Недостатком Грэхема является необходимость сортировки всех точек по полярному углу, что занимает достаточно много времени . Джарвис требует перебора всех точек для каждой из точек оболочки, что в худшем случае занимает .
Описание Алгоритма
- Разобьем все множество на произвольные группы по штук в каждой. Будем считать, что нам известно. Тогда всего групп окажется .
- Для каждой группы запускаем Грехема.
- Начиная с самой нижней точки ищем саму выпуклую оболочку Джарвисом, но перебираем не все точки, а по одной из каждой группы.
Сложность
На втором шаге алгоритма в каждой группе оболочка ищется за , общее время - . На третьем шаге поиск каждой следующей точки в каждой группе занимает , так как точки уже отсортированы, и мы можем найти нужную бинпоиском. Тогда поиск по всем группам займет . Всего таких шагов будет , значит общее время - . Итоговое время - . Несложно видеть, что минимум достигается при . В таком случае сложность равна .
Поиск
Как заранее узнать ? Воспользуемся следующим методом. Положим . Начиная с маленьких будем запускать наш алгоритм, причем если на третьем шаге Джарвис уже сделал шагов, то мы выбрали наше слишком маленьким, будем увеличивать, пока не станет . Тогда общее время алгоритма -
Ссылки
Алгоритм QuickHull
Описание Алгоритма
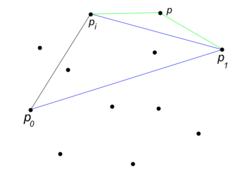
- Найдем самую левую точку и самую правую точку (Если таких несколько, выберем среди таких нижнюю и верхнюю соответственно).
- Возьмем все точки выше прямой .
- Найдем среди этого множества точку , наиболее отдаленную от прямой (если таких несколько, взять самую правую).
- Рекурсивно повторить шаги 2-3 для прямых и , пока есть точки.
- Добавить в ответ точки , полученные в п. 3.
- Повторить пункты 2-5 для (то есть для "нижней" половины).
- Ответ - объединение списков из п. 5 для верхней и нижней половины.
Корректность
Очевидно, что выпуклая оболочка всего множества является объединением выпуклых оболочек для верхнего и нижнего множества. Докажем, что алгоритм верно строит оболочку для верхнего множества, для нижнего рассуждения аналогичны. Точки и принадлежат оболочке.
- Пусть какая-то точка входит в нашу оболочку, но не должна.
Назовем эту точку . По алгоритму эта точка появилась как самая удаленная от некой прямой . Так как не входит в оболочку, то существует прямая из настоящей выпуклой оболочки, что лежит снизу от прямой. Тогда какая-то из и удалена от прямой дальше , что противоречит алгоритму.
- Наоборот, пусть какой-то точки в нашей оболочке нет, а должна быть.
Пойдем вниз рекурсии в те ветки, где есть . В какой-то момент окажется внутри некоторого треугольника. Но тогда возникает противоречие с тем, что принадлежит выпуклой оболочке.
Таким образом, наша оболочка совпадает с истинной, а значит алгоритм корректен.
Реализация
Заметим, что длина высоты, опущенная из точки на отрезок , пропорциональна векторному произведению , поэтому для сравнения можно использовать именно это. Векторное произведение эквивалентно предикату поворота, поэтому можно так же использовать и его.
Псевдокод
Inplace-реализация алгоритма. - исходное множество. - рекурсивная функция, находящая оболочку подмножества . В реализации в конце каждого подмножества находятся эл-ты, точно не принадлежащие оболочке.
QuickHull(S) find i such that S[i] has the highest x-coordinate and lowest y-coordinate swap(S[1], S[i]) find i such that S[i] has the lowest x-coordinate and lowest y-coordinate swap(S[n], S[i]) k = partition1(S) // разбиваем на те эл-ты, которые лежат над прямой и на остальные a = quick_hull(S, 1, k) b = quick_hull(S, k + 1, n); swap(S[a..k], S[k + 1, b]) return start + (a - 1) + (b - k - 1)
quick_hull(S, start, end) find i such that S[i], S[start], S[end] has maximum value (a, b) = partition2(S, start, end, S[i]) //свапаем эл-ты S так, чтобы сначала были все эл-ты над прямой S[start]S[i], потом S[i]S[end], потом все остальное c = quick_hull(S, start, a) d = quick_hull(S, a + 1, b) swap(S[c..a], S[a + 1..d]) return start + (a - c) + (d - b)
Сложность
Пусть время, необходимое для нахождения оболочки над некой прямой и множеством точек есть Тогда , где - множества над полученными прямыми. Отсюда видно, что в худшем случае, алгоритм тратит . На рандомных же данных это число равно