Теорема Турана об экстремальном графе — различия между версиями
| Строка 1: | Строка 1: | ||
==Теорема Турана== | ==Теорема Турана== | ||
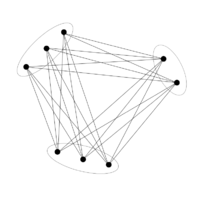
| − | '''Теорема Ту́рана''' (англ. ''Turán's theorem'') {{---}} классическая теорема экстремальной теории графов. Она послужила образцом для большого количества подобных теорем, которые изучают некоторые глобальные параметры, такие как [[Раскраска графа| хроматическое число]], относительно присутствия тех или иных подструктур. | + | [[Файл:Turan example.png|200px|thumb|right|Пример графа Турана при <tex>n = 8, r = 4</tex>]] |
| + | '''Теорема Ту́рана''' (англ. ''Turán's theorem'') {{---}} классическая теорема экстремальной теории графов. Она послужила образцом для большого количества подобных теорем, которые изучают некоторые глобальные параметры, такие как [[Раскраска графа| хроматическое число]], относительно присутствия тех или иных подструктур. | ||
Впервые задачу сформулировал Пал Туран в 1941 году. | Впервые задачу сформулировал Пал Туран в 1941 году. | ||
| Строка 8: | Строка 9: | ||
<tex>ex(n, K^r)</tex> {{---}} максимальное количество ребер в графе на <tex>n</tex> вершинах, которые не содержит <tex>K^r</tex> как подграф. | <tex>ex(n, K^r)</tex> {{---}} максимальное количество ребер в графе на <tex>n</tex> вершинах, которые не содержит <tex>K^r</tex> как подграф. | ||
}} | }} | ||
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Граф Турана''' <tex>T^{r-1}(n)</tex> {{---}} единственный полный <tex>(r - 1)</tex>-дольный полный граф на <tex>n > r-1</tex> вершинах, доли которого по мощности не отличаются более чем на 1. Если | + | '''Граф Турана''' <tex>T^{r-1}(n)</tex> {{---}} единственный полный <tex>(r - 1)</tex>-дольный полный граф на <tex>n > r-1</tex> вершинах, доли которого по мощности не отличаются более чем на 1. Если <tex>n \leqslant r - 1</tex>, то <tex>T^{r-1}(n) = K^n</tex>. Через <tex> t_{r-1}(n) </tex> обозначим количество ребер в <tex>T^{r-1}(n)</tex>. |
| − | <tex>n \leqslant r - 1</tex>, то <tex>T^{r-1}(n) = K^n</tex>. | + | }} |
| − | }} | ||
| − | + | {{Лемма | |
| − | {{ | + | |statement= |
| − | | | + | Среди <tex>(r - 1)</tex>-дольных графов <tex>T^{r-1}(n)</tex> имеет максимальное количество ребер. |
| − | <tex> | + | |proof= |
| + | Пусть есть существует максимальный <tex>(r - 1)</tex>-дольный граф, в котором есть две доли <tex>V_1 и V_2 \ | \ |V_1| - |V_2| > 1</tex>. Но тогда перекинув одну вершину из <tex>V_1</tex> в <tex>V_2</tex>, количество ребер увеличится. Противоречие. | ||
}} | }} | ||
| − | |||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
Для всех целых чисел <tex>r</tex>, <tex>n</tex>, где <tex>r > 1</tex>, любой граф <tex>G \nsubseteq K^r</tex> с <tex>n</tex> вершинами и <tex>ex(n, K^r)</tex> ребрами есть <tex>T^{r-1}(n)</tex>. | Для всех целых чисел <tex>r</tex>, <tex>n</tex>, где <tex>r > 1</tex>, любой граф <tex>G \nsubseteq K^r</tex> с <tex>n</tex> вершинами и <tex>ex(n, K^r)</tex> ребрами есть <tex>T^{r-1}(n)</tex>. | ||
|proof= | |proof= | ||
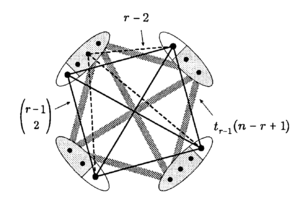
| + | [[Файл:Turan theorem induction step.png|300px|thumb|left|Шаг индукции]] | ||
| + | Применим индукцию по <tex>n</tex>. | ||
| + | |||
| + | '''База:''' | ||
| − | + | При <tex>n \le r - 1</tex> имеем <tex>G = K^n = T^{r-1}(n)</tex>, что и утверждалось База доказана. | |
| − | + | '''Шаг индукции:''' | |
| − | <tex> | + | Пусть теперь <tex>n \ge r</tex>. |
| + | Поскольку <tex>G</tex> реберно-максимален и не содержит подграфа <tex>K^r</tex>, то <tex>G</tex> содержит подграф <tex>K^{r-1}</tex>. Обозначим любой из них как <tex>K</tex>. Тогда индукционному предположению <tex>G - K</tex> имеет не более <tex>t_{r-1}(n - r + 1)</tex> ребер, а любая вершина <tex>G - K</tex> имеет не более <tex>r - 2</tex> соседей в <tex>K</tex>. Следовательно: | ||
| − | + | <tex>|E(G)| \le \underbrace{t_{r-1}(n + r - 1)}_{G-K} + \underbrace{(n - r + 1)(r - 2)}_{(G-K) \rightleftarrows (K)} + \underbrace{{r-1 \choose 2}}_{K} = t_{r-1}(n); (1)</tex> | |
| − | |||
| − | + | Равенство справа следует непосредственно из графа Турана <tex>T^{r-1}(n)</tex>. | |
| − | <tex> | + | Поскольку <tex>G</tex> экстремален для <tex>K^r</tex>, то в <tex>(1)</tex> имеет место равенство. Таким образом, любая вершина из <tex>G - K</tex> имеет ровно <tex>r - 2</tex> соседа в <tex>K</tex> {{---}} точно также, как и вершины <tex>x_1,\cdots, x_{r-1}</tex> из самого <tex>K</tex>. |
| − | есть множество всех вершин <tex>G</tex>, чьи <tex>r - 2</tex> соседей в <tex>K</tex> | + | При <tex>i = 1,\cdots, r-1</tex> пусть <tex>V_i := \{v \in V(G)\ |\ vx_i \not\in E(G)\}</tex> есть множество всех вершин <tex>G</tex>, чьи <tex>r - 2</tex> соседей в <tex>K</tex> отличны от <tex>x_i</tex>. |
| + | Так как каждая вершина <tex>G - K</tex> имеет ровно <tex>r - 2</tex> соседа в <tex>K</tex>, то все <tex>V_i</tex> не зависимы. При этом они в объединении дают <tex>V(G)</tex> поскольку <tex>K^r \nsubseteq G</tex>. Следовательно, граф <tex>G</tex> является <tex>(r-1)</tex>-дольным. | ||
| + | Так как по Лемме <tex>T^{r-1}(n)</tex> {{---}} единственный <tex>(r-1)</tex>-дольный граф с <tex>n</tex> вершинами и максимальными числом ребер, наше утверждение, что <tex>G = T^{r-1}(n)</tex>, следует из предположения об экстремальности <tex>G</tex>. | ||
}} | }} | ||
Версия 21:58, 27 декабря 2017
Теорема Турана
Теорема Ту́рана (англ. Turán's theorem) — классическая теорема экстремальной теории графов. Она послужила образцом для большого количества подобных теорем, которые изучают некоторые глобальные параметры, такие как хроматическое число, относительно присутствия тех или иных подструктур.
Впервые задачу сформулировал Пал Туран в 1941 году.
| Определение: |
| — максимальное количество ребер в графе на вершинах, которые не содержит как подграф. |
| Определение: |
| Граф Турана — единственный полный -дольный полный граф на вершинах, доли которого по мощности не отличаются более чем на 1. Если , то . Через обозначим количество ребер в . |
| Лемма: |
Среди -дольных графов имеет максимальное количество ребер. |
| Доказательство: |
| Пусть есть существует максимальный -дольный граф, в котором есть две доли . Но тогда перекинув одну вершину из в , количество ребер увеличится. Противоречие. |
| Теорема: |
Для всех целых чисел , , где , любой граф с вершинами и ребрами есть . |
| Доказательство: |
|
Применим индукцию по . База: При имеем , что и утверждалось База доказана. Шаг индукции: Пусть теперь . Поскольку реберно-максимален и не содержит подграфа , то содержит подграф . Обозначим любой из них как . Тогда индукционному предположению имеет не более ребер, а любая вершина имеет не более соседей в . Следовательно:
Равенство справа следует непосредственно из графа Турана . Поскольку экстремален для , то в имеет место равенство. Таким образом, любая вершина из имеет ровно соседа в — точно также, как и вершины из самого . При пусть есть множество всех вершин , чьи соседей в отличны от . Так как каждая вершина имеет ровно соседа в , то все не зависимы. При этом они в объединении дают поскольку . Следовательно, граф является -дольным. Так как по Лемме — единственный -дольный граф с вершинами и максимальными числом ребер, наше утверждение, что , следует из предположения об экстремальности . |
См. также
Источники информации
Дистель, Рейнград. Теория графов: Пер. с англ. — Новосибирск: Изд-во Ин-та математики, 2002. — 166-170 стр. — ISBN 5-86134-101-X.