Тонкая куча — различия между версиями
Genyaz (обсуждение | вклад) (Амортизационный анализ операций) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 25 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''''' | + | '''Тонкая куча''' (англ. ''Thin heap'') {{---}} структура данных, реализующая приоритетную очередь с теми же асимптотическими оценками, что и [[Фибоначчиева куча|фибоначчиева куча]], но имеющая большую практическую ценность из-за меньших констант. |
| − | + | Тонкие кучи, как и многие другие [[Двоичная куча|кучеобразные]] структуры, аналогичны [[Биномиальная куча|биномиальным кучам]]. | |
= Тонкое дерево = | = Тонкое дерево = | ||
| + | |||
{{Определение | {{Определение | ||
| − | |id=thin_tree_def | + | |id=thin_tree_def |
| − | |definition='''Тонкое дерево''' ('' | + | |definition='''Тонкое дерево''' (англ. ''Thin tree'') <tex>T_k</tex> ранга <tex>k</tex> {{---}} это дерево, которое может быть получено из [[Биномиальная куча#Биномиальное дерево|биномиального дерева]] <tex>B_k</tex> удалением самого левого сына у нескольких внутренних, то есть не являющихся корнем или листом, узлов. |
}} | }} | ||
| − | + | Ограничение на принадлежность внутренним узлам вызвано тем, что у листьев детей нет, а если у корня <tex>B_k</tex> удалить самого левого сына, то <tex>B_k</tex> превратится в <tex>B_{k-1}</tex>. | |
| + | |||
| + | {{Утверждение | ||
| + | |id=about_thin_tree_rank | ||
| + | |statement=Ранг тонкого дерева равен количеству детей его корня. | ||
| + | }} | ||
| − | Для любого узла <tex>x</tex> в дереве <tex>T_k</tex> обозначим: <tex>Degree(x)</tex> {{---}} количество детей узла <tex>x</tex> | + | Для любого узла <tex>x</tex> в дереве <tex>T_k</tex> обозначим: |
| + | * <tex>\mathtt{Degree(x)}</tex> {{---}} количество детей узла <tex>x</tex>. | ||
| + | * <tex>\mathtt{Rank(x)}</tex> {{---}} ранг соответствующего узла в [[Биномиальная куча#Биномиальное дерево|биномиальном дереве]] <tex>B_k</tex>. | ||
== Свойства тонкого дерева == | == Свойства тонкого дерева == | ||
{{Утверждение | {{Утверждение | ||
| − | |id=about_thin_tree | + | |id=about_thin_tree |
| − | |statement=Тонкое дерево обладает следующими | + | |statement=Тонкое дерево обладает следующими свойствами: |
| − | # Для любого узла <tex>x</tex> либо <tex>Degree(x)=Rank(x)</tex>, в этом случае говорим, что узел <tex>x</tex> не | + | # Для любого узла <tex>x</tex> либо <tex>\mathtt{Degree(x)=Rank(x)}</tex>, в этом случае говорим, что узел <tex>x</tex> не тонкий (полон); либо <tex>\mathtt{Degree(x)=Rank(x)-1}</tex>, в этом случае говорим, что узел <tex>x</tex> тонкий (не полон). |
| − | # Корень не | + | # Корень не тонкий (полон). |
| − | # Для любого узла <tex>x</tex> ранги его детей от самого правого к самому левому равны соответственно <tex>0,1,2,...,Degree(x)-1</tex>. | + | # Для любого узла <tex>x</tex> ранги его детей от самого правого к самому левому равны соответственно <tex>\mathtt{0,1,2,...,Degree(x)-1}</tex>. |
| − | # Узел <tex>x</tex> | + | # Узел <tex>x</tex> тонкий тогда и только тогда, когда его ранг на 2 больше, чем ранг его самого левого сына, или его ранг равен 1, и он не имеет детей. |
}} | }} | ||
| − | = Тонкая куча = | + | [[Файл:Thin_trees.png|200x200px|слева|frame|Из [[Биномиальная куча#Биномиальное дерево|биномиального дерева]] ранга 3 получены два тонких дерева. Числа обозначают ранги узлов, закрашенные вершины являются тонкими (не имеют самого левого сына)]] |
| + | <br clear="all" /> | ||
| + | |||
| + | == Тонкая куча == | ||
{{Определение | {{Определение | ||
| − | |id=thin_forest_def | + | |id=thin_forest_def |
| − | |definition='''Тонкий лес''' ('' | + | |definition='''Тонкий лес''' (англ. ''Thin forest'') {{---}} это набор тонких деревьев, ранги которых не обязательно попарно различны. |
}} | }} | ||
{{Утверждение | {{Утверждение | ||
| − | |id=about_thin_forest_with_n_nodes | + | |id=about_thin_forest_with_n_nodes |
|statement=Для любого натурального числа <tex>n</tex> существует тонкий лес, который содержит ровно <tex>n</tex> элементов и состоит из тонких деревьев попарно различных рангов. | |statement=Для любого натурального числа <tex>n</tex> существует тонкий лес, который содержит ровно <tex>n</tex> элементов и состоит из тонких деревьев попарно различных рангов. | ||
| − | |proof=Действительно, любой биномиальный лес является тонким, а для биномиального леса рассматриваемое утверждение справедливо. | + | |proof=Действительно, любой [[Биномиальная куча#Биномиальное дерево|биномиальный лес]] является тонким, а для биномиального леса рассматриваемое утверждение справедливо. |
}} | }} | ||
{{Определение | {{Определение | ||
| − | |id=thin_heap_def | + | |id=thin_heap_def |
| − | |definition='''Тонкая куча''' ('' | + | |definition='''Тонкая куча''' (англ. ''Thin heap'') {{---}} это [[Двоичная куча|кучеобразно]] нагруженный тонкий лес, то есть каждое тонкое дерево удовлетворяет условиям [[Двоичная куча|кучи]]. |
}} | }} | ||
| Строка 43: | Строка 54: | ||
{{Теорема | {{Теорема | ||
| − | |id=max_rank_th | + | |id=max_rank_th |
|about=О максимальном ранге узла | |about=О максимальном ранге узла | ||
| − | |statement=В тонкой куче из <tex>n</tex> элементов <tex>D(n) \leqslant \log_{\Phi} n</tex>, где <tex | + | |statement=В тонкой куче из <tex>n</tex> элементов <tex>D(n) \leqslant \log_{\Phi} n</tex>, где <tex>\varphi=\dfrac{1+\sqrt{5}}{2}</tex> {{---}} золотое сечение. |
| − | |proof=Сначала покажем, что узел ранга <tex>k</tex> в тонком дереве имеет не менее <tex>F_k \geqslant \ | + | |proof=Сначала покажем, что узел ранга <tex>k</tex> в тонком дереве имеет не менее <tex>F_k \geqslant \varphi^{k-1}</tex> потомков, включая самого себя, где <tex>F_k</tex> — <tex>k</tex>-е число Фибоначчи. |
| + | |||
| + | Действительно, пусть <tex>T_k</tex> {{---}} минимально возможное число узлов, включая самого себя, в тонком дереве ранга <tex>k</tex>. По свойствам <tex>1</tex> и <tex>3</tex> тонкого дерева получаем следующие соотношения: | ||
| − | + | <tex>T_0=1,T_1=1,T_k \geqslant 1+\sum\limits_{i=0}^{k-2}T_i</tex> для <tex>k \geqslant 2</tex> | |
| − | <tex> | + | Числа Фибоначчи удовлетворяют этому же рекуррентному соотношению, причем неравенство можно заменить равенством. Отсюда по индукции следует, что <tex>T_k \geqslant F_k</tex> для любых <tex>k</tex>. Неравенство <tex>F_k \geqslant \varphi^{k-1}</tex> [[Фибоначчиева куча#Лемма3|хорошо известно]]. |
| − | + | Теперь убедимся в том, что максимально возможный ранг <tex>D(n)</tex> тонкого дерева в тонкой куче, содержащей <tex>n</tex> элементов, не превосходит числа <tex>\log_{\varphi}(n)+1</tex>. | |
| − | + | Действительно, выберем в тонкой куче дерево максимального ранга. Пусть <tex>n^*</tex> {{---}} количество вершин в этом дереве, тогда <tex>n \geqslant n^* \geqslant \varphi^{D(n)-1}</tex>. | |
| − | Отсюда следует, что <tex>D(n)\leqslant\log_{\ | + | Отсюда следует, что <tex>D(n)\leqslant\log_{\varphi}(n)+1</tex>. |
}} | }} | ||
| − | == | + | == Структура == |
| − | + | === Структура узла === | |
| − | + | '''struct''' Node | |
| − | + | '''int''' key <span style="color:#008000"> // ключ</span> | |
| − | + | '''int''' rank <span style="color:#008000"> // ранг узла</span> | |
| − | + | '''Node''' child <span style="color:#008000"> // указатель на самого левого ребенка узла</span> | |
| − | + | '''Node''' right <span style="color:#008000"> // указатель на правого брата узла, либо на следующий корень, если текущий узел корень</span> | |
| − | + | '''Node''' left <span style="color:#008000"> // указатель на левого брата узла, либо на родителя, если текущий узел самый левый, либо null, если это корень</span> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Для ускорения проверки на тонкость (англ. ''thinness'') можно отдельно хранить тонкость вершины. | ||
Также в вершине можно хранить любую дополнительную информацию. | Также в вершине можно хранить любую дополнительную информацию. | ||
| + | === Структура кучи === | ||
| + | '''struct''' ThinHeap | ||
| + | '''Node''' first <span style="color:#008000"> // указатель на корень дерева с минимальным ключом</span> | ||
| + | '''Node''' last <span style="color:#008000"> // указатель на последний корень</span> | ||
== Операции над тонкой кучей == | == Операции над тонкой кучей == | ||
Рассмотрим операции, которые можно производить над тонкой кучей. Время работы указано в таблице: | Рассмотрим операции, которые можно производить над тонкой кучей. Время работы указано в таблице: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Многие операции над тонкой кучей выполняются так же, как и над фиббоначиевой. | + | {| class="wikitable" style="width:10cm" border=1 |
| + | |+ | ||
| + | |-align="center" bgcolor=#EEEEFF | ||
| + | ! Операция || Время работы | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | |<tex>\mathrm{makeHeap}</tex>||<tex>O(1)</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | |<tex>\mathrm{insert}</tex>||<tex>O(1)</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | ||<tex>\mathrm{getMin}</tex>||<tex>O(1)</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | |<tex>\mathrm{merge}</tex>||<tex>O(1)</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | |<tex>\mathrm{extractMin}</tex>||<tex>O(\log(n))</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | |<tex>\mathrm{decreaseKey}</tex>||<tex>O(1)</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | |<tex>\mathrm{delete}</tex>||<tex>O(\log(n))</tex> | ||
| + | |} | ||
| + | |||
| + | Многие операции над тонкой кучей выполняются так же, как и над [[Фибоначчиева куча|фиббоначиевой]]. | ||
| − | Для амортизационного анализа применим метод потенциалов. | + | Для [[Амортизационный анализ|амортизационного анализа]] операций применим [[Амортизационный анализ#Метод потенциалов|метод потенциалов]]. |
| − | Пусть функция потенциала определена как <tex>\Phi = n + 2 \cdot m</tex> где <tex>n</tex> {{---}} это количество | + | Пусть функция потенциала определена как <tex>\Phi = n + 2 \cdot m</tex> где <tex>n</tex> {{---}} это количество тонких деревьев в куче, а <tex>m</tex> {{---}} это количество тонких вершин. |
{{Утверждение | {{Утверждение | ||
| − | |id=about_thin_heap_potential | + | |id=about_thin_heap_potential |
|statement=Определённый таким образом потенциал обладает свойствами: | |statement=Определённый таким образом потенциал обладает свойствами: | ||
# <tex>\Phi \geqslant 0</tex>. | # <tex>\Phi \geqslant 0</tex>. | ||
| − | # Для пустой кучи <tex>\Phi = 0</tex>. | + | # Для пустой тонкой кучи <tex>\Phi = 0</tex>. |
}} | }} | ||
| + | |||
| + | Пусть <tex>\mathtt{Node}</tex> {{---}} узел тонкого дерева, а <tex>\mathtt{ThinHeap}</tex> {{---}} тонкая куча, причём <tex>\mathtt{ThinHeap}</tex> содержит ссылки на первый и последний корень <tex>\mathtt{first}</tex> и <tex>\mathtt{last}</tex> соответственно. | ||
| + | |||
| + | Также введем вспомогательную функцию проверки узла на тонкость, для этого воспользуемся тем, что у левого сына узла <tex>x</tex> ранг равен <tex>\mathtt{Degree(x) - 1}</tex>. | ||
| + | |||
| + | <code> | ||
| + | '''bool''' isThin(x: '''Node'''): | ||
| + | '''if''' x.rank == 1 | ||
| + | '''return''' x.child == ''null'' | ||
| + | '''else''' | ||
| + | '''return''' x.child.rank + 1 != x.rank | ||
| + | </code> | ||
| − | |||
=== makeHeap === | === makeHeap === | ||
| + | Для создания новой пустой тонкой кучи нужно вернуть ссылку на новый пустой корневой список, его потенциал <tex>\Phi=0</tex>. | ||
| − | + | <code> | |
| + | '''ThinHeap''' makeHeap(): | ||
| + | H.first = ''null'' | ||
| + | H.last = ''null'' | ||
| + | '''return''' H | ||
| + | </code> | ||
Стоимость <tex>O(1)</tex>. | Стоимость <tex>O(1)</tex>. | ||
| Строка 125: | Строка 151: | ||
=== insert === | === insert === | ||
| − | + | Для вставки элемента в тонкую кучу нужно создать новое тонкое дерево из единственного узла <tex>x</tex> с ключом <tex>x.key</tex>, добавить его в корневой список на первое место, если этот ключ минимален, либо на последнее. Потенциал <tex>\Phi</tex> увеличивается на 1. | |
| + | |||
| + | <code> | ||
| + | '''void''' insert(H: '''ThinHeap''', x: '''Node'''): | ||
| + | '''if''' H.first == ''null'' | ||
| + | H.first = x | ||
| + | H.last = x | ||
| + | '''else''' | ||
| + | '''if''' x.key < H.first.key | ||
| + | x.right = H.first | ||
| + | H.first = x | ||
| + | '''else''' | ||
| + | H.last.right = x | ||
| + | H.last = x | ||
| + | </code> | ||
Стоимость <tex>O(1)</tex>. | Стоимость <tex>O(1)</tex>. | ||
| Строка 131: | Строка 171: | ||
=== getMin === | === getMin === | ||
| − | + | Для обращения к минимальному элементу в тонкой куче нужно обратиться к первому корневому узлу списка и вернуть его ключ, потенциал <tex>\Phi</tex> не меняется. | |
| + | |||
| + | <code> | ||
| + | '''Node''' getMin(H: '''ThinHeap'''): | ||
| + | '''return''' H.first | ||
| + | </code> | ||
Стоимость <tex>O(1)</tex>. | Стоимость <tex>O(1)</tex>. | ||
| − | === | + | === merge === |
| + | |||
| + | Для объединения тонких куч нужно слить их корневые списки, ставя первым тот список, у которого ключ первого корня минимален. Суммарный потенциал <tex>\Phi</tex> не меняется. | ||
| − | + | <code> | |
| + | '''ThinHeap''' merge(H1: '''ThinHeap''', H2: '''ThinHeap'''): | ||
| + | '''if''' H1.first == ''null'' | ||
| + | '''return''' H2 | ||
| + | '''else''' | ||
| + | '''if''' H2.first == ''null'' | ||
| + | '''return''' H1 | ||
| + | '''else''' | ||
| + | '''if''' H1.first.key < H2.first.key | ||
| + | H1.last.right = H2.first | ||
| + | H1.last = H2.last | ||
| + | '''return''' H1 | ||
| + | '''else''' | ||
| + | H2.last.right = H1.first | ||
| + | H2.last = H1.last | ||
| + | '''return''' H2 | ||
| + | </code> | ||
Стоимость <tex>O(1)</tex>. | Стоимость <tex>O(1)</tex>. | ||
=== extractMin === | === extractMin === | ||
| + | Чтобы извлечь минимальный элемент из тонкой кучи нужно: | ||
| + | # Удалить корень с минимальным ключом из корневого списка. | ||
| + | # Уменьшить ранг для всех его тонких детей. | ||
| + | # Cлить детей с корневым списком. | ||
| + | # Объединять, пока возможно, тонкие деревья одного ранга. | ||
| − | + | Это можно сделать, например, с помощью вспомогательного массива размером <tex>O(D(n))</tex>, в <tex>i</tex>-ой ячейке которого хранится корень тонкого дерева <tex>T_i</tex> ранга <tex>i</tex>. | |
| − | |||
| − | |||
| − | |||
| − | Это можно сделать, например, с помощью вспомогательного массива размером <tex>O(D(n))</tex>, в <tex>i</tex>-ой ячейке | ||
Изначально массив пуст, а мы добавляем в него все деревья нашего корневого списка. | Изначально массив пуст, а мы добавляем в него все деревья нашего корневого списка. | ||
| − | При добавлении нового дерева мы, | + | При добавлении нового дерева мы, если дерево такого ранга уже есть в массиве, связываем его с существующим и пытаемся добавить новое дерево с рангом на <tex>1</tex> больше. |
| + | |||
| + | <code> | ||
| + | '''Node''' extractMin(H: '''ThinHeap'''): | ||
| + | <span style="color:#008000">// Удаляем минимальный корень из корневого списка</span> | ||
| + | tmp = H.first | ||
| + | H.first = H.first.right | ||
| + | '''if''' H.first == ''null'' | ||
| + | H.last = ''null'' | ||
| + | <span style="color:#008000">// Снимаем тонкость с его детей и добавляем их в корневой список</span> | ||
| + | x = tmp.first.child | ||
| + | '''while''' x != ''null'' | ||
| + | '''if''' isThin(x) | ||
| + | x.rank = x.rank - 1 | ||
| + | x.left = ''null'' | ||
| + | next = x.right | ||
| + | insert(H, x) | ||
| + | x = next | ||
| + | <span style="color:#008000">// Объединяем все корни одного ранга с помощью вспомогательного массива aux</span> | ||
| + | max = -1 | ||
| + | x = H.first | ||
| + | '''while''' x != ''null'' | ||
| + | '''while''' aux[x.rank] != ''null'' | ||
| + | next = x.right | ||
| + | '''if''' aux[x.rank].key < x.key | ||
| + | swap(aux[x.rank], x) | ||
| + | aux[x.rank].right = x.child | ||
| + | x.child.left = aux[x.rank] | ||
| + | aux[x.rank].left = x | ||
| + | x.child = aux[x.rank] | ||
| + | aux[x.rank] = ''null'' | ||
| + | x.rank = x.rank + 1 | ||
| + | aux[x.rank] = x | ||
| + | '''if''' x.rank > max | ||
| + | max = x.rank | ||
| + | x = next | ||
| + | <span style="color:#008000">// Собираем все корни обратно в тонкую кучу</span> | ||
| + | H = makeHeap() | ||
| + | i = 0 | ||
| + | '''while''' i <= max | ||
| + | insert(H, aux[i]) | ||
| + | i = i + 1 | ||
| + | '''return''' tmp | ||
| + | </code> | ||
| − | Пусть мы сделали <tex>ls</tex> | + | Пусть мы сделали <tex>ls</tex> связывающих шагов (англ. ''linking steps'') во время добавления в массив. |
| − | Мы удалили корень из списка за <tex>O(1)</tex>, затем за <tex>O(D(n))</tex> нормализовали детей корня и добавили в корневой список, | + | Мы удалили корень из списка за <tex>O(1)</tex>, затем за <tex>O(D(n))</tex> нормализовали детей корня и добавили в корневой список, далее за <tex>O(D(n))+ls</tex> получили новый корневой список, в котором за <tex>O(D(n))</tex> нашли минимальный корень и подвесили список за него. |
| − | Получили фактическую стоимость <tex>O(D(n))+ | + | Получили фактическую стоимость <tex>O(D(n))+ls</tex>. С другой стороны, при добавлении детей в список мы увеличили потенциал <tex>\Phi</tex> не более чем на <tex>O(D(n))</tex>, а каждый связывающий шаг уменьшает наш потенциал <tex>\Phi</tex> на <tex>1</tex>. Отсюда стоимость <tex>O(D(n))=O(\log(n))</tex>. |
| − | + | Стоимость <tex>O(\log(n))</tex>. | |
=== decreaseKey === | === decreaseKey === | ||
| + | После уменьшения ключа может быть нарушена [[Двоичная куча|кучеобразность]], в этом случае мы переносим все поддерево с корнем в уменьшаемом элементе в корневой список, также обновляем минимум в тонкой куче. | ||
| + | |||
| + | Теперь могут быть нарушены свойства тонкого дерева, будем различать два вида нарушений: | ||
| + | * Братские нарушения {{---}} это нарушения [[Тонкая куча#about_thin_tree|третьего свойства]] тонкого дерева. | ||
| + | * Родительские нарушения {{---}} это нарушения [[Тонкая куча#about_thin_tree|первого или второго свойства]] тонкого дерева. | ||
| + | |||
| + | Назовем узел <tex>y</tex> узлом локализации братского нарушения среди детей узла <tex>z</tex>, если ранг узла <tex>y</tex> отличается от ранга его ближайшего правого брата на 2, либо он не имеет правого брата и его ранг равен 1. | ||
| + | |||
| + | Назовем узел <tex>y</tex> узлом локализации родительского нарушения, если выполнено одно из трех условий: | ||
| + | # Ранг узла <tex>y</tex> на три больше, чем ранг его самого левого сына. | ||
| + | # Ранг узла <tex>y</tex> равен двум, и он не имеет детей. | ||
| + | # Узел <tex>y</tex> есть тонкий корень дерева. | ||
| + | |||
| + | Пусть узел <tex>y</tex> — это узел локализации братского нарушения. | ||
| + | * Узел <tex>y</tex> не тонкий, тогда помещаем поддерево с корнем в самом левом сыне узла <tex>y</tex> на место пропущенного в братском списке. Узел <tex>y</tex> становится тонким, дерево становится корректным, процедура исправления завершается. | ||
| + | * Узел <tex>y</tex> тонкий, тогда уменьшаем ранг узла <tex>y</tex> на единицу. Теперь узлом локализации нарушения будет либо левый брат узла <tex>y</tex>, либо его родитель, тогда нарушение станет родительским. | ||
| + | |||
| + | С помощью этих действий мы избавились от братских нарушений, теперь разберем родительские. | ||
| + | |||
| + | Пусть узел <tex>y</tex> — это узел локализации родительского нарушения, а узел <tex>z</tex> — родитель узла <tex>y</tex>. | ||
| + | |||
| + | Переместим все поддерево с корнем в <tex>y</tex> в корневой список и уменьшим ранг <tex>y</tex>. | ||
| + | # Если узел <tex>y</tex> не был старшим братом, то переходим к его левому брату, нарушение станет братским. | ||
| + | # Если узел <tex>y</tex> был старшим братом, то смотрим на родителя | ||
| + | #* Узел <tex>z</tex> не был тонким, пометим его как тонкий, тогда дерево станет корректным. | ||
| + | #* Узел <tex>z</tex> был тонким, тогда <tex>z</tex> {{---}} новый узел локализации родительского нарушения, переходим к нему. | ||
| + | |||
| + | Продолжая эту процедуру, мы или остановимся, или дойдем до корня дерева, тогда достаточно сделать ранг корня на 1 больше ранга его самого левого сына. | ||
| + | |||
| + | Каждый промежуточный шаг рекурсии уменьшает количество тонких узлов на 1 и добавляет не более одного дерева в корневой список, тогда на каждом промежуточном шаге потенциал уменьшается минимум на 1, отсюда амортизированная стоимость <tex>O(1)</tex>. Также заметим, что мы всегда перемещаемся либо влево, либо вверх по нашему дереву, так что суммарно в худшем случае мы выполним <tex>O(\log(n))</tex> операций, а не <tex>O(n)</tex>, как в случае фибоначчиевой кучи. | ||
Стоимость <tex>O(1)</tex>. | Стоимость <tex>O(1)</tex>. | ||
=== delete === | === delete === | ||
| − | + | Чтобы удалить элемент из тонкой кучи нужно сначала выполнить <tex>\mathtt{decreaseKey}</tex> этого элемента до <tex>-\infty</tex>, а затем выполнить <tex>\mathtt{extractMin}</tex>. | |
| + | |||
| + | <code> | ||
| + | '''void''' delete(H: '''ThinHeap''', x: '''Node'''): | ||
| + | decreaseKey(H, x, <tex>-\infty</tex>) | ||
| + | extractMin() | ||
| + | </code> | ||
Стоимость <tex>O(\log(n))</tex>. | Стоимость <tex>O(\log(n))</tex>. | ||
| − | |||
= Источники = | = Источники = | ||
| + | * [http://dl.acm.org/citation.cfm?id=1328914 ''Каплан Х.'', ''Тарьян А. Р..'', Thin Heaps, Thick Heaps // ACM Transactions on Algorithms. {{---}} 2008. {{---}} Т.4. {{---}} №1. {{---}} C. 1{{---}}14. {{---}} ISSN: 1549-6325] | ||
| + | * [http://www.lektorium.tv/lecture/?id=14233 ''Станкевич А. С.'', Дополнительные главы алгоритмов, лекция 1 {{---}} Лекториум] | ||
* [http://www.intuit.ru/studies/courses/100/100/lecture/1542 Тонкие кучи — INTUIT.ru] | * [http://www.intuit.ru/studies/courses/100/100/lecture/1542 Тонкие кучи — INTUIT.ru] | ||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Структуры данных]] | ||
[[Категория: Приоритетные очереди]] | [[Категория: Приоритетные очереди]] | ||
Текущая версия на 19:42, 4 сентября 2022
Тонкая куча (англ. Thin heap) — структура данных, реализующая приоритетную очередь с теми же асимптотическими оценками, что и фибоначчиева куча, но имеющая большую практическую ценность из-за меньших констант.
Тонкие кучи, как и многие другие кучеобразные структуры, аналогичны биномиальным кучам.
Содержание
Тонкое дерево
| Определение: |
| Тонкое дерево (англ. Thin tree) ранга — это дерево, которое может быть получено из биномиального дерева удалением самого левого сына у нескольких внутренних, то есть не являющихся корнем или листом, узлов. |
Ограничение на принадлежность внутренним узлам вызвано тем, что у листьев детей нет, а если у корня удалить самого левого сына, то превратится в .
| Утверждение: |
Ранг тонкого дерева равен количеству детей его корня. |
Для любого узла в дереве обозначим:
- — количество детей узла .
- — ранг соответствующего узла в биномиальном дереве .
Свойства тонкого дерева
| Утверждение: |
Тонкое дерево обладает следующими свойствами:
|
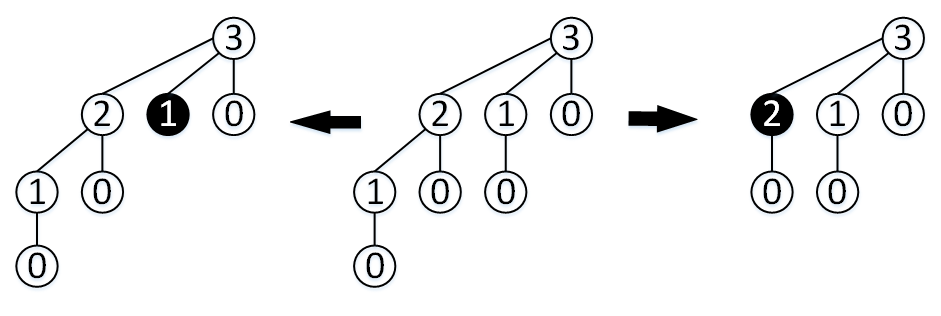
Тонкая куча
| Определение: |
| Тонкий лес (англ. Thin forest) — это набор тонких деревьев, ранги которых не обязательно попарно различны. |
| Утверждение: |
Для любого натурального числа существует тонкий лес, который содержит ровно элементов и состоит из тонких деревьев попарно различных рангов. |
| Действительно, любой биномиальный лес является тонким, а для биномиального леса рассматриваемое утверждение справедливо. |
| Определение: |
| Тонкая куча (англ. Thin heap) — это кучеобразно нагруженный тонкий лес, то есть каждое тонкое дерево удовлетворяет условиям кучи. |
Пусть — максимально возможный ранг узла в тонкой куче, содержащей элементов.
| Теорема (О максимальном ранге узла): |
В тонкой куче из элементов , где — золотое сечение. |
| Доказательство: |
|
Сначала покажем, что узел ранга в тонком дереве имеет не менее потомков, включая самого себя, где — -е число Фибоначчи. Действительно, пусть — минимально возможное число узлов, включая самого себя, в тонком дереве ранга . По свойствам и тонкого дерева получаем следующие соотношения: для Числа Фибоначчи удовлетворяют этому же рекуррентному соотношению, причем неравенство можно заменить равенством. Отсюда по индукции следует, что для любых . Неравенство хорошо известно. Теперь убедимся в том, что максимально возможный ранг тонкого дерева в тонкой куче, содержащей элементов, не превосходит числа . Действительно, выберем в тонкой куче дерево максимального ранга. Пусть — количество вершин в этом дереве, тогда . Отсюда следует, что . |
Структура
Структура узла
struct Node int key // ключ int rank // ранг узла Node child // указатель на самого левого ребенка узла Node right // указатель на правого брата узла, либо на следующий корень, если текущий узел корень Node left // указатель на левого брата узла, либо на родителя, если текущий узел самый левый, либо null, если это корень
Для ускорения проверки на тонкость (англ. thinness) можно отдельно хранить тонкость вершины. Также в вершине можно хранить любую дополнительную информацию.
Структура кучи
struct ThinHeap Node first // указатель на корень дерева с минимальным ключом Node last // указатель на последний корень
Операции над тонкой кучей
Рассмотрим операции, которые можно производить над тонкой кучей. Время работы указано в таблице:
| Операция | Время работы |
|---|---|
Многие операции над тонкой кучей выполняются так же, как и над фиббоначиевой.
Для амортизационного анализа операций применим метод потенциалов.
Пусть функция потенциала определена как где — это количество тонких деревьев в куче, а — это количество тонких вершин.
| Утверждение: |
Определённый таким образом потенциал обладает свойствами:
|
Пусть — узел тонкого дерева, а — тонкая куча, причём содержит ссылки на первый и последний корень и соответственно.
Также введем вспомогательную функцию проверки узла на тонкость, для этого воспользуемся тем, что у левого сына узла ранг равен .
bool isThin(x: Node):
if x.rank == 1
return x.child == null
else
return x.child.rank + 1 != x.rank
makeHeap
Для создания новой пустой тонкой кучи нужно вернуть ссылку на новый пустой корневой список, его потенциал .
ThinHeap makeHeap(): H.first = null H.last = null return H
Стоимость .
insert
Для вставки элемента в тонкую кучу нужно создать новое тонкое дерево из единственного узла с ключом , добавить его в корневой список на первое место, если этот ключ минимален, либо на последнее. Потенциал увеличивается на 1.
void insert(H: ThinHeap, x: Node):
if H.first == null
H.first = x
H.last = x
else
if x.key < H.first.key
x.right = H.first
H.first = x
else
H.last.right = x
H.last = x
Стоимость .
getMin
Для обращения к минимальному элементу в тонкой куче нужно обратиться к первому корневому узлу списка и вернуть его ключ, потенциал не меняется.
Node getMin(H: ThinHeap): return H.first
Стоимость .
merge
Для объединения тонких куч нужно слить их корневые списки, ставя первым тот список, у которого ключ первого корня минимален. Суммарный потенциал не меняется.
ThinHeap merge(H1: ThinHeap, H2: ThinHeap):
if H1.first == null
return H2
else
if H2.first == null
return H1
else
if H1.first.key < H2.first.key
H1.last.right = H2.first
H1.last = H2.last
return H1
else
H2.last.right = H1.first
H2.last = H1.last
return H2
Стоимость .
extractMin
Чтобы извлечь минимальный элемент из тонкой кучи нужно:
- Удалить корень с минимальным ключом из корневого списка.
- Уменьшить ранг для всех его тонких детей.
- Cлить детей с корневым списком.
- Объединять, пока возможно, тонкие деревья одного ранга.
Это можно сделать, например, с помощью вспомогательного массива размером , в -ой ячейке которого хранится корень тонкого дерева ранга .
Изначально массив пуст, а мы добавляем в него все деревья нашего корневого списка.
При добавлении нового дерева мы, если дерево такого ранга уже есть в массиве, связываем его с существующим и пытаемся добавить новое дерево с рангом на больше.
Node extractMin(H: ThinHeap): // Удаляем минимальный корень из корневого списка tmp = H.first H.first = H.first.right if H.first == null H.last = null // Снимаем тонкость с его детей и добавляем их в корневой список x = tmp.first.child while x != null if isThin(x) x.rank = x.rank - 1 x.left = null next = x.right insert(H, x) x = next // Объединяем все корни одного ранга с помощью вспомогательного массива aux max = -1 x = H.first while x != null while aux[x.rank] != null next = x.right if aux[x.rank].key < x.key swap(aux[x.rank], x) aux[x.rank].right = x.child x.child.left = aux[x.rank] aux[x.rank].left = x x.child = aux[x.rank] aux[x.rank] = null x.rank = x.rank + 1 aux[x.rank] = x if x.rank > max max = x.rank x = next // Собираем все корни обратно в тонкую кучу H = makeHeap() i = 0 while i <= max insert(H, aux[i]) i = i + 1 return tmp
Пусть мы сделали связывающих шагов (англ. linking steps) во время добавления в массив.
Мы удалили корень из списка за , затем за нормализовали детей корня и добавили в корневой список, далее за получили новый корневой список, в котором за нашли минимальный корень и подвесили список за него.
Получили фактическую стоимость . С другой стороны, при добавлении детей в список мы увеличили потенциал не более чем на , а каждый связывающий шаг уменьшает наш потенциал на . Отсюда стоимость .
Стоимость .
decreaseKey
После уменьшения ключа может быть нарушена кучеобразность, в этом случае мы переносим все поддерево с корнем в уменьшаемом элементе в корневой список, также обновляем минимум в тонкой куче.
Теперь могут быть нарушены свойства тонкого дерева, будем различать два вида нарушений:
- Братские нарушения — это нарушения третьего свойства тонкого дерева.
- Родительские нарушения — это нарушения первого или второго свойства тонкого дерева.
Назовем узел узлом локализации братского нарушения среди детей узла , если ранг узла отличается от ранга его ближайшего правого брата на 2, либо он не имеет правого брата и его ранг равен 1.
Назовем узел узлом локализации родительского нарушения, если выполнено одно из трех условий:
- Ранг узла на три больше, чем ранг его самого левого сына.
- Ранг узла равен двум, и он не имеет детей.
- Узел есть тонкий корень дерева.
Пусть узел — это узел локализации братского нарушения.
- Узел не тонкий, тогда помещаем поддерево с корнем в самом левом сыне узла на место пропущенного в братском списке. Узел становится тонким, дерево становится корректным, процедура исправления завершается.
- Узел тонкий, тогда уменьшаем ранг узла на единицу. Теперь узлом локализации нарушения будет либо левый брат узла , либо его родитель, тогда нарушение станет родительским.
С помощью этих действий мы избавились от братских нарушений, теперь разберем родительские.
Пусть узел — это узел локализации родительского нарушения, а узел — родитель узла .
Переместим все поддерево с корнем в в корневой список и уменьшим ранг .
- Если узел не был старшим братом, то переходим к его левому брату, нарушение станет братским.
- Если узел был старшим братом, то смотрим на родителя
- Узел не был тонким, пометим его как тонкий, тогда дерево станет корректным.
- Узел был тонким, тогда — новый узел локализации родительского нарушения, переходим к нему.
Продолжая эту процедуру, мы или остановимся, или дойдем до корня дерева, тогда достаточно сделать ранг корня на 1 больше ранга его самого левого сына.
Каждый промежуточный шаг рекурсии уменьшает количество тонких узлов на 1 и добавляет не более одного дерева в корневой список, тогда на каждом промежуточном шаге потенциал уменьшается минимум на 1, отсюда амортизированная стоимость . Также заметим, что мы всегда перемещаемся либо влево, либо вверх по нашему дереву, так что суммарно в худшем случае мы выполним операций, а не , как в случае фибоначчиевой кучи.
Стоимость .
delete
Чтобы удалить элемент из тонкой кучи нужно сначала выполнить этого элемента до , а затем выполнить .
void delete(H: ThinHeap, x: Node):
decreaseKey(H, x, )
extractMin()
Стоимость .