Участник:Kabanov — различия между версиями
Kabanov (обсуждение | вклад) |
Kabanov (обсуждение | вклад) м (→4.5 Взаимосвязь алгоритмов Дейкстры и A*) |
||
| (не показано 17 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Также как и алгоритм Эппштейна, K* выполняет поиск пути на графе <tex>G</tex> и использует граф путей <tex>P(G)</tex>. Граф путей ищется с помощью алгоритма Дейкстры для того, чтобы вычислить пути <tex>s-t</tex> в виде последовательности запасных путей. Общий принцип работы алгоритма K* следующий: | |
| − | + | 1) K* применяет A* на графе <tex>G</tex> вместо обратного алгоритма Дейкстры, который используется алгоритмом Эппштейна. | |
| − | | | + | 2) Мы запускаем A* на <tex>G</tex> и Дейкстру на <tex>P(G)</tex> в поочередном порядке, который позволяет Дейкстре вычислить требуемые пути до заверешения полного поиска алгоритма A* на графе <tex>G</tex> . |
| − | + | ||
| − | + | == 4.1 Поиск A* на G == | |
| + | K* применяет A* к входному графу <tex>G</tex> для того, чтобы построить дерево поиска <tex>T</tex>. Заметим, что A*, также как и алгоритм Дейкстры, строит дерево поиска в процессе нахождения кратчайшего пути <tex>s-t</tex> . Эти деревья формируются с помощью ссылок на родительские узлы, которые хранятся в том время, как A* производит итерации для того, чтобы восстановить путь <tex>s-t</tex>, когда вершина <tex>t</tex> ещё не найдена. Запасные ребра, открытые в процессе поиска A* на графе G, немедленно добавляются в граф P(G), структура которого будет объясняться в разделе 4.3. | ||
| + | |||
| + | В K* A* применяется к графу <tex>G</tex> в прямом направлении в отличие от алгоритма Эппштейна, из-за чего корнем дерева <tex>T</tex> является вершина начальная <tex>s</tex>. Это необходимо для того, чтобы была возможность работать c неявным описанием графа <tex>G</tex> через функцию successor (функция, возвращающая список исходящих ребер из данной вершины). На протяжение статьи будем считать граф <tex>G</tex> конечным, если не будет сказано иное. Заметим, что А* корректен на конечных графах. Будем следовать литературному соглашению, предполагая, что стоимость бесконечного пути неограниченна. | ||
| + | |||
| + | == 4.2 Стоимость объезда == | ||
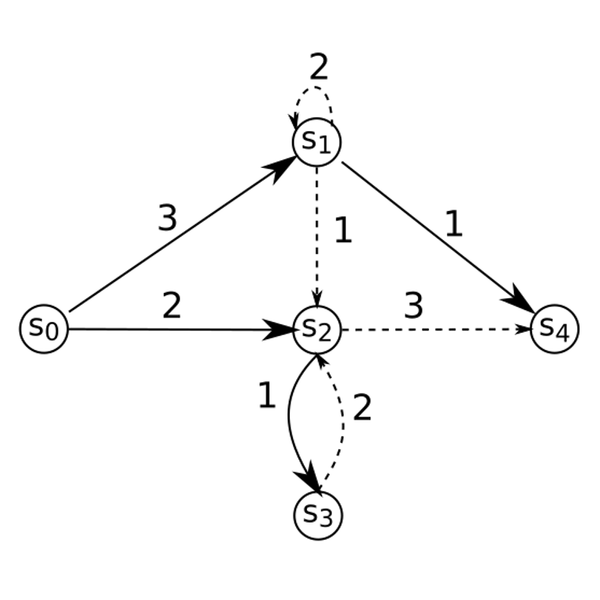
| + | [[Файл:kstar-figure-3.png|600px|thumb|center|'''Рисунок 3.''' Исходный граф, в котором сплошные линии представляют построенное A* дерево поиска <tex>T</tex>. Пунктирные линии являются запасными ребрами.]] | ||
| + | Для ребра <tex>(u, v)</tex> стоимость '''объезда''' (англ. ''detour'') <tex>\delta(u, v)</tex> представляет стоимость '''ущерба''' (англ. ''disadvantage'') из-за взятия ребра объезда <tex>(u,v)</tex> в сравнении с кратчайшим путем <tex>s-t</tex> через <tex>v</tex>. Ни длина кратчайшего пути <tex>s-t</tex> через <tex>v</tex>, ни длина пути <tex>s-t</tex>, включающего запасные ребра <tex>(u, v)</tex> не известны, когда A* обнаруживает <tex>(u, v)</tex>. Обе длины могут быть оценены с помощью функции оценки <tex>f</tex>, которая использует эвристическую функцию <tex>h</tex>. Пусть <tex>f(v)</tex> будет <tex>f</tex>-значением с соответствии с деревом поиска <tex>T</tex> и <tex>f_u(v)</tex> будет <tex>f</tex>-значением в соответствии с родителем u, т.е. <tex>f_u(v) = g(u) + c(u, v) + h(v)</tex>. Тогда <tex>\delta(u, v)</tex> может быть определена так: | ||
| + | |||
| + | <tex>\delta(u, v) = f_u(v) - f(v) = g(u) + c(u, v) + h(v) - g(v) - h(v) = g(u) + c(u, v) - g(v)</tex> | ||
| + | |||
| + | Заметим, что <tex>\delta(u, v)</tex> дает точную объездную метрику, поскольку оценочное <tex>h</tex>-значение не появляется в определении функции <tex>\delta(u, v)</tex>. | ||
| + | |||
| + | == 4.3 Структура графа путей == | ||
| + | Структура графа путей <tex>P(G)</tex> довольно сложная. В принципе, <tex>P(G)</tex> будет ориентированным графом, вершины которого соответствуют ребрам в исходном графе <tex>G</tex>. Он будет организован как коллекция взаимосвязанных '''куч''' (англ. ''heap''). 2 бинарные кучи минимума присвоены к каждой вершине <tex>v</tex> в графе <tex>G</tex>, которые называются '''входящей кучей''' (англ. ''incoming heap'')<tex>H_{in}(v)</tex> и '''деревянной кучей''' (англ. ''tree heap'') <tex>H_{T}(v)</tex>. Эти кучи являются базисом <tex>P(G)</tex>. Как мы покажем далее, использование этих куч также играет главную роль в поддержании асимптотической сложности K*, также как в EA и LVEA. | ||
| + | |||
| + | Входящая куча <tex>H_{in}(v)</tex> содержит узлы для каждого запасного ребра к вершине <tex>v</tex>, которые до сих пор были обнаружены A*. Узлы <tex>H_{in}(v)</tex> будут упорядочены в соответствии с <tex>\delta</tex>-значением соответствующих переходов. Узел владеющий ребром с минимальной стоимостью ущерба будет расположен на вершине кучи. Мы ограничим структуру кучи <tex>H_{in}(v)</tex> таким образом, что её корень в отличие от остальных узлов, будет иметь не более 1 ребенка. Обозначим его <tex>root_{in}(v)</tex>. | ||
| + | |||
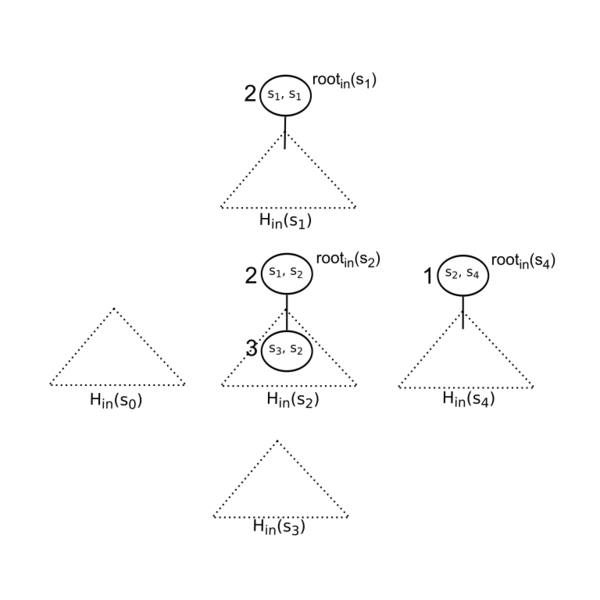
| + | '''Пример 4.''' Рисунок 4 иллюстрирует входящие кучи графа из рисунка 3. Цифры рядом с узлами кучи соответствуют <tex>\delta</tex>-значениям. | ||
| + | |||
| + | [[Файл:kstar-figure-4.png|600px|thumb|center|'''Рисунок 4.''' Входящие кучи <tex>H_{in}(s_i)</tex>, полученные из графа, показанного на рисунке 3.]] | ||
| + | |||
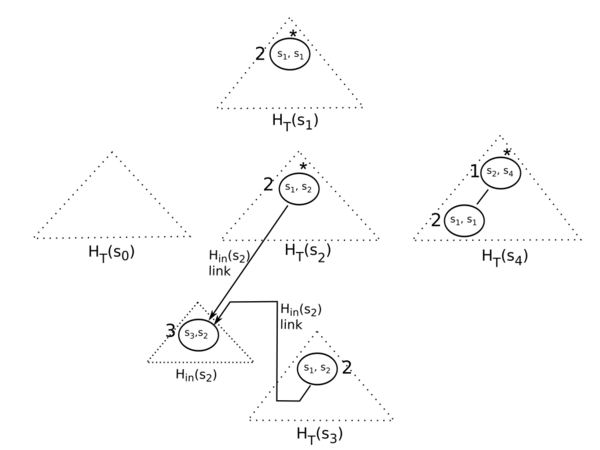
| + | Деревянная куча <tex>H_{T}(v)</tex> для произвольной вершины <tex>v</tex> строится следующим образом. Если <tex>v</tex> - стартовая вершина, т.е. <tex>v = s</tex>, то <tex>H_{T}(v)</tex> будет изначально пустой кучей. Затем в неё будет добавлен <tex>root_{in}(s)</tex>, если <tex>H_{in}(s)</tex> не пустая. Если <tex>v</tex> не стартовая вершина, то пусть вершина <tex>u</tex> будет родителем вершины <tex>v</tex> в дереве поиска <tex>T</tex>. Мы можем представить, что <tex>H_{T}(v)</tex> конструируется как копия <tex>H_{T}(u)</tex>, в которую добавлен <tex>root_{in}(v)</tex>. Если <tex>H_{in}(v)</tex> пустая, то <tex>H_{T}(v)</tex> идентична <tex>H_{T}(u)</tex>. Однако, для экономии памяти мы создаем только дешевую копию <tex>H_{T}(u)</tex>. Это осуществляется через создание копий только тех узлов кучи, которые лежат на обновленном пути в <tex>H_{T}(u)</tex>. Оставшаяся часть <tex>H_{T}(u)</tex> не копируется. Другими словами, <tex>root_{in}(v)</tex> вставляется в <tex>H_{T}(u)</tex> неразрушающим путем так, что структура <tex>H_{T}(u)</tex> сохраняется. В куче <tex>H_{T}(v)</tex> к <tex>root_{in}(v)</tex> могут быть присоединены 1 или 2 ребенка. К тому же, <tex>root_{in}(v)</tex> хранит только 1 собственного ребенка из <tex>H_{in}(v)</tex>. Мы обозначим корень <tex>H_{T}(v)</tex> как <tex>R(v)</tex>. | ||
| + | |||
| + | [[Файл:kstar-figure-5.png|600px|thumb|center|'''Рисунок 5.''' Деревянные кучи <tex>H_{T}(s_i)</tex>, полученные из графа, показанного на рисунке 3.]] | ||
| + | |||
| + | Назовем ребра, которые берут начало из входящих или деревянных куч, '''кучными ребрами''' (англ. ''heap edges''). Сформулируем следующую лемму. | ||
| + | {{Лемма | ||
| + | |about=1 | ||
| + | |statement=Все узлы, достижимые из <tex>R(v)</tex> по кучным ребрам, для каждой вершины <tex>v</tex> формируют тернарную кучу, упорядоченную в соответствии с <tex>\delta</tex>-значением. Мы назовем такую кучу '''графовой кучей''' (англ. ''graph heap'') вершины <tex>v</tex> и обозначим её как <tex>H_{G}(v)</tex>. | ||
| + | |proof=Те узлы, которые находятся в <tex>H_{T}(v)</tex> или во входящей куче, на которую ссылается узел из <tex>H_{T}(v)</tex>, достижимы по кучным ребрам из <tex>R(v)</tex>. Деревянная куча <tex>H_{T}(v)</tex> формируется через добавление корней входящих куч всех вершин, лежащих на пути из стартовой вершины <tex>s</tex> до <tex>v</tex> в бинарной куче. Каждый из этих корней имеет максимум 3 детей: до 2 в <tex>H_{T}(v)</tex> и дополнительно единственного из входящей кучи. Любой другой узел, живущий во входящей куче имеет не больше 2 детей. Напомним, что каждая входящая куча - это бинарная куча с ограничением, что корень имеет единственного ребенка. Древовидная структура <tex>H_{G}(v)</tex> непосредственный результат древовидных структур <tex>H_{T}(v)</tex> и входящих куч. Более того, кучная характеристика деревянной кучи обеспечивает упорядочивание в соответствии с <tex>\delta</tex>-значением по ребрам из <tex>H_{T}(v)</tex>, а кучная характеристика входящих куч - по всем ребрам из <tex>H_{in}</tex>. Все это приводит к тому, что <tex>H_{G}(v)</tex> - тернарная куча, упорядоченная в соответствии с <tex>\delta</tex>-значением. | ||
}} | }} | ||
| − | {{ | + | Финальная структура <tex>P(G)</tex> получется из входящих и деревянных куч следующим образом. К каждому узлу <tex>n</tex> из <tex>P(G)</tex>, несущему ребро <tex>(u,v)</tex>, мы присоединим указатель, ссылающийся на <tex>R(u)</tex>, который является корневым узлом <tex>H_{T}(u)</tex>. Мы назовем такие указатели '''кросс-ребрами''' (англ. ''cross edges''), в то время как указатели, возникающие из куч названы кучными ребрами, как упоминалось раньше. Более того, мы добавим специальный узел <tex>\mathrm{R}</tex> в <tex>P(G)</tex> с одним выходящим кросс-ребром к <tex>R(t)</tex>. |
| − | + | ||
| − | + | Более того, мы определим весовую функцию <tex>\Delta</tex> на ребрах из <tex>P(G)</tex>. Пусть <tex>(n,n')</tex> обозначает ребро в <tex>P(G)</tex>, и пусть <tex>e</tex> и <tex>e'</tex> обозначают ребра из <tex>G</tex>, соответствующие узлам <tex>n</tex> и <tex>n'</tex>. Тогда определим <tex>\Delta(n,n')</tex> следующим образом: | |
| − | } | + | |
| + | <tex> | ||
| + | \Delta(n,n')=\begin{cases} | ||
| + | \delta(e') - \delta(e),& \text{if}\ (n,n')\ \text{heap edge} \\ | ||
| + | \delta(e'),& \text{if}\ (n,n')\ \text{cross edge}. | ||
| + | \end{cases} | ||
| + | </tex> | ||
| + | Лемма 1 подразумевает, что куча упорядоченная в соответствии с <tex>\delta</tex>-значанием поддерживается для любого кучного ребра из <tex>P(G)</tex>. Эта упорядочивание кучи подразумевает, что <tex>\Delta(n,n')</tex> неотрицательна для любого кучного ребра <tex>(n,n')</tex>. Следовательно, <tex>\Delta</tex> также неотрицательна, т.е. <tex>\Delta(n,n') >= 0</tex> для любого ребра <tex>(n,n')</tex> в <tex>P(G)</tex>. Стоимость пути <tex>\sigma</tex>, т.е. <tex>C_{P(G)}(\sigma)</tex> равна <tex>\sum_{e \in \sigma}\Delta(e)</tex>. | ||
| − | + | '''Пример 6.''' | |
| − | |||
| − | |||
| − | + | В оставшейся части этого раздела мы проиллюстрируем особенности структуры графа путей, которые актуальны для нахождения кратчайших путей <tex>s-t</tex>. | |
| − | |||
| − | + | Первое наблюдение в том, что <tex>P(G)</tex> ориентированный взвешенный граф. Каждый узел в <tex>P(G)</tex> несет запасное ребро из G. Использование бинарных куч в конструкции <tex>P(G)</tex> извлекает выгоду из следующих 2 свойств. Во-первых, произвольный узел в <tex>P(G)</tex> имеет не более 4 выходящих ребер. Одним из ребер будет точно кросс-ребро в то время, как оставшимися будут кучные ребра. Во-вторых, функция веса <tex>\Delta</tex> неотрицательна. Как станет ясно в разделе 5, эти свойства необходимы для доказательства правильности и определения сложности K*. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Второе наблюдение заключается в существовании соответствия один-к-одному между путей <tex>s-t</tex> в <tex>G</tex> и путей в <tex>Р(G)</tex>, которые начинаются в <tex>\mathrm{R}</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ... | |
| − | + | {{Лемма | |
| + | |about=2 | ||
| + | |statement=Пусть <tex>n</tex> будет узлом графовой кучи <tex>H_{G}(w)</tex> для какой-нибудь вершины <tex>w</tex>. Пусть <tex>(u,v)</tex> будет ребром связанным с <tex>n</tex>. Тогда существует путь в дереве поиска <tex>T</tex> из <tex>v</tex> в <tex>w</tex>. | ||
| + | |proof=... | ||
}} | }} | ||
| − | == | + | == 4.4 Алгоритмическая структура K* == |
| − | + | Алгоритмический принцип K* следующий. Будем запускать алгоритмы Дейкстры и A* на <tex>G</tex> с чередованием. Сначала, мы выполним A* на <tex>G</tex>, который будет работать до тех, пока вершина <tex>t</tex> не будет выбрана из очереди для раскрытия. Затем, вы запустим алгоритм Дейкстры на доступной части <tex>P(G)</tex>. Каждый узел раскрытый Дейкстрой представляет путь. Если точнее, то путь <tex>\sigma</tex> в <tex>P(G)</tex>, по которому Дейкстра достигла этого узла является решением. Путь <tex>s-t</tex> может быть построен из <tex>\sigma</tex> за линейное время путем вычисления последовательности запасных ребер <tex>seq(\sigma)</tex> и затем <tex>s-t</tex> пути из неё. Если Дейкстра находит <tex>k</tex> кратчайших путей, то K* завершается успешно. Иначе, A* возобновляется для исследования большей части <tex>G</tex>. Это приводит к росту <tex>P(G)</tex>, на котором алгоритм Дейкстры затем будет возобновлен. Мы будем повторять этот процесс до тех пор, пока алгоритм Дейкстры не найдет <tex>k</tex> кратчайших путей. | |
| − | + | Data: A graph given by its start vertex s ∈ V and its successor function succ and a | |
| − | + | natural number k | |
| + | Result: A list R containing k sidetrack edge sequences representing k solution paths | ||
| − | + | 1 <tex>open_D</tex> ← пустая приоритетная очередь | |
| − | + | 2 <tex>closed_D</tex> ← пустая хеш-таблица | |
| − | + | 3 <tex>R</tex> ← пустой список | |
| + | 4 <tex>P(G)</tex> ← пустой граф путей | ||
| + | 5 Выполняем A* на графе <tex>G</tex> пока <tex>t</tex> не будет выбрана для раскрытия | ||
| + | 6 Если вершина <tex>t</tex> не была достигнута, то выходим без ответа | ||
| + | 7 Кладем <tex>\mathrm{R}</tex> в очередь <tex>open_D</tex> | ||
| + | 8 '''while''' A queue or open D is not empty: | ||
| + | 9 '''if''' A queue is not empty: | ||
| + | 10 '''if''' очередь <tex>open_D</tex> не пуста: | ||
| + | 11 Let u be the head of the search queue of A ∗ and n the head of <tex>open_D</tex> | ||
| + | 12 <tex>d = max\{ d(n) + \Delta(n, n') | n' \in succ(n) \}</tex> | ||
| + | 13 '''if''' <tex>g(t) + d <= f</tex> (u) then переходим на строку 17. | ||
| + | 14 Возобновляем A* для того, чтобы исследовать более большую часть графа <tex>G</tex> | ||
| + | 15 Обновляем <tex>P(G)</tex> and bring Dijkstra’s search into a consistent status | ||
| + | 16 Переходим на строку 8 | ||
| + | 17 '''if''' очередь <tex>open_D</tex> пуста: переходим на строку 8. | ||
| + | 18 Remove from <tex>open_D</tex> and place on <tex>closed_D</tex> the node n with the minimal d-value. | ||
| + | 19 '''foreach''' <tex>n'</tex> referred by n in P(G): | ||
| + | 20 <tex>d(n') = d(n) + \Delta(n, n')</tex> | ||
| + | 21 Attach to <tex>n'</tex> a parent link referring to <tex>n</tex>. | ||
| + | 22 Insert n 0 into <tex>open_D</tex> | ||
| + | 23 Пусть <tex>\sigma</tex> будет путем в <tex>P(G)</tex>, через который узел n был достигнут. | ||
| + | 24 Добавим <tex>seq(\sigma)</tex> в конец списка <tex>R</tex>. | ||
| + | 25 '''if''' <tex>|R| = k</tex>: переходим на строку 26. | ||
| + | 26 Return R and exit. | ||
| − | + | Алгоритм 1 содержит псевдокод K*. Код с 8 по 25 строчку образует главный цикл K*. Цикл завершается, когда очереди обоих алгоритмов А* и Дейкстры пусты. До 8 строчки выполняет некоторые подготовительные вещи. После инициализации, А* запускает на 5 строчке пока вершина <tex>t</tex> не будет выбрана им для рассмотрения, в этом случае кратчайший путь <tex>s-t</tex> будет найден. Если <tex>t</tex> не достигнута, то алгоритм завершается без ответа. Отметим, что он не завершится на бесконечных графах. Иначе, алгоритм добавляет специальную вершину <tex>R</tex>, которая назначена корнем <tex>P(G)</tex>, в поисковую очередь алгоритма Дейкстры. Затем, K* входит в главный цикл. | |
| − | |||
| − | + | K* поддерживает механизм планирования для контролирования, когда A* или Дейкстра будет возобновлены. Если очередь из A* не пуста, что означает, что А* ещё не завершил исследования всего графа G, то Дейкстра возобновляется тогда и только тогда, когда <tex>g(t) + d <= f(u)</tex>. Значение <tex>d</tex> является максимальным <tex>d</tex>-значением среди всех successor-ов головы поисковой очереди <tex>n</tex> алгоритма Дейкстры. Вершина <tex>u</tex> является головой поисковой очереди A*. Напомним, что <tex>d</tex> - функция расстояния, используемая в алгоритме Дейкстры. Если очередь поиска Дейкстры пуста или <tex>g(t) + d > f(u)</tex>, то А* возобновляется для того, чтобы исследовать более большую часть графа <tex>G</tex> (строка 14). То, как долго мы ему позволим работать, является компромиссом. Если мы запустим его только на маленьком количестве шагов, то мы дадим Дейкстре шанс найти необходимое количество путей скорее, чем они будут доступны в <tex>P(G)</tex>. С другой стороны, мы вызываем накладные расходы путем переключения A* и Дейкстры и поэтому должны ограничить количество переключений. Эти накладные расходы вызваны тем фактом, что после возобновления A* (строка 14), структура графа <tex>P(G)</tex> может измениться. Следовательно нам необходимо обновить <tex>P(G)</tex> (строка 15), как мы будет широко обсуждать в разделе 4.5. Это требует последующую проверку статуса Дейкстры. Мы должны быть уверены, что Дейкстра поддерживает согласованное состояние после изменений в <tex>P(G)</tex>. K* предусматривает условие, которые управляет решением, когда остановить A*, которое мы назовем ''условие расширения''. Для того, чтобы поддерживать аналогичную асимптотическую сложность как у EA и LVEA, мы должны определить условие расширения так, чтобы A* выполнялся пока количество рассмотренных вершин и количество внутренних ребер удваивается или <tex>G</tex> полностью исследован. Мы обсудим эту проблему несколько подробнее позже. В качестве полезного свойства, K* позволяет другое определения этого условия, которое может быть более эффективным на практике. В наших экспериментах в разделе 6, мы определили условие расширения так, что количество рассмотренных вершин или количество рассмотренных ребер ребер возрастает на 20% при каждом запуске A*. Этот механизм планирования включен до тех пор, пока A* не закончит исследовать весь граф <tex>G</tex>. Как только A* исследует весь граф <tex>G</tex> (строка 9), механизм планирования отключается и в дальнейшем работает только алгоритм Дейкстры. | |
| − | + | Строки 18-22 представляют обычный шаг рассмотрения узла алгоритмом Дейкстры. Отметим, что когда successor-узел <tex>n'</tex> сгенерирован, K* не проверяет был ли <tex>n'</tex> уже посещен до этого. Другими словами, каждый раз, когда узел генерируется, он рассматривает как новый. Эта стратегия обоснована на наблюдении, что путь s-t может содержать одно и то же ребро несколько раз. Строка 24 добавляет следующий путь <tex>s-t</tex> в результирующее множество R. Это делается путем конструирования последовательности запасных ребер <tex>seq(\sigma)</tex> из пути <tex>\sigma</tex>, через которые Дейкстра достигла узла <tex>n</tex>, который был только что рассмотрен. Алгоритм завершается, когда в результирующее множество добавлено <tex>k</tex> последовательностей запасных ребер (строка 25). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == 4.5 Взаимосвязь алгоритмов Дейкстры и A* == | |
| + | Тот факт, что оба алгоритма A* и Дейкстры делят между собой граф путей <tex>P(G)</tex>, вызывает обеспокоенность в отношении правильности работы Дейкстры на <tex>P(G)</tex>. Возобновление A* приводит к изменениям в структуре <tex>P(G)</tex>. Таким образом, после возобновления A*, мы обновляем <tex>P(G)</tex> и проверяет статус поиска Дейкстры (строка 15). В основном, A* может добавить новые узлы, менять <tex>\delta</tex>-значения существующих узлов или даже удалять узлы. A* может также существенно изменять дерево поиска <tex>T</tex>, которое будет в худшем случае разрушать структуру все деревянных куч <tex>H_{T}</tex>. Эти изменения могут приводить к глобальной реструктуризации или даже перестроению <tex>P(G)</tex> с нуля. В худшем случае это может сделать предыдущие поиски Дейкстры на <tex>P(G)</tex> бесполезными таким образом, что нам придется перезапускать алгоритм Дейкстры с нуля. | ||
| − | + | Если использованная эвристическая оценка допустимая, то наше положение лучше. Нам по-прежнему может понадобится перестроение <tex>P(G)</tex>, но мы покажем, что это перестроение не мешает корректности поиска Дейкстры на <tex>P(G)</tex>. Другими словами, мы не теряем результаты, до сих пор полученные поиском Дейкстры. | |
| − | + | В случае монотонной эвристической оценки мы даже не нуждаемся в восстановлении или перестроении <tex>P(G)</tex>. Если <tex>h</tex> монотонная, то дерево поиска A* является деревом кратчайшего пути для всех раскрытых вершин. Следовательно, g-значения раскрытых вершин не меняются. Это означает, что <tex>\delta</tex>-значения для внутренних ребер никогда не изменятся. Ребра дерева раскрытых вершин не изменятся также. Следовательно, обновление <tex>\delta</tex>-значений, heaping-up, heaping-down (операции в кучах) или удаление узлов не влекут за собой каких-либо изменений в <tex>P(G)</tex>. Только добавление новых узлов приводит к изменениям в <tex>P(G)</tex>. Следовательно, восстановление или глобальное перестроение не требуется в данном случае. | |
| − | |||
| − | |||
| − | + | В оставшейся части этого раздела, мы сначала покажем, что корректность поиска Дейкстры на <tex>P(G)</tex> поддерживается в случае допустимой эвристической оценки. После этого мы покажем, что изменения в <tex>P(G)</tex> могут помешать завершенности поиска Дейкстры независимо от того, является ли эвристика допустимой или даже монотонной. Следовательно, мы предложим механизм для её поддержания. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Мы фокусируемся дальше на корректности поиска Дейкстры на <tex>P(G)</tex> в случае допустимой эвристической оценки. Сначала, мы заявляем, что если <tex>h</tex> допустимая, то узлы исследованной части <tex>P(G)</tex> не поменяют свои <tex>\delta</tex>-значения. | |
| − | + | {{Лемма | |
| − | + | |about=6 | |
| − | + | |statement=Пусть <tex>n</tex> будет произвольным узлов в <tex>P(G)</tex> и пусть <tex>(u,v)</tex> будет ребром, связанным с <tex>n</tex>. Если <tex>h</tex> допустимая функция, то значение <tex>\delta(u, v)</tex> никогда не изменится после того, как <tex>n</tex> будет рассмотрен алгоритмом Дейкстры. | |
| − | + | |proof=... | |
| + | }} | ||
| − | + | Из леммы 6 мы может вывести следующее следствие. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Лемма | {{Лемма | ||
| − | |statement= | + | |about=следствие 3 |
| − | + | |statement=Пусть <tex>n</tex> будет произвольным узлом в <tex>P(G)</tex>. Если <tex>h</tex> допустимая функция, то <tex>n</tex> никогда не будет удален из <tex>P(G)</tex> после того, как <tex>n</tex> был рассмотрен алгоритмом Дейкстры. | |
| − | + | |proof=... | |
| − | + | }} | |
| − | + | Более того, мы докажем, что структура исследованной части <tex>P(G)</tex> не изменится. | |
| − | + | {{Лемма | |
| + | |about=7 | ||
| + | |statement=Пусть <tex>n</tex> будет произвольным узлов в <tex>P(G)</tex>. Если <tex>h</tex> допустимая функция, то <tex>n</tex> никогда не изменит свою позицию после того, как он был рассмотрен алгоритмом Дейкстры. | ||
| + | |proof=... | ||
| + | }} | ||
| − | + | Леммы 6 и 7 обеспечивают, что изменения в <tex>P(G)</tex>, которые индуцируются A*, не влияют на часть <tex>P(G)</tex>, которую алгоритм Дейкстры уже исследовал. Это гарантирует корректность поиска Дейкстры на <tex>P(G)</tex>, если используемая эвристика допустимая. Таким образом, каждый путь, который предоставляет алгоритм Дейкстры корректен и его длина действительна. Однако, это не обеспечивает завершенность поиска Дейкстры на <tex>P(G)</tex>. | |
| − | |||
| − | |||
| − | |||
| − | + | Возможно, что узел <tex>n'</tex> присоединяется к другом узлу n как ребенок, после раскрытия узла <tex>n</tex>. В этом случае братья <tex>n'</tex> будут рассотрены до того, как <tex>n'</tex> станет ребенком n. Поэтому мы должны рассмотреть то, что было упущено во время поиска в связи с отсутствием <tex>n'</tex>. Мы добиваемся этого путем применения строк 20-22 к <tex>n'</tex> для каждого раскрытого направленного predecessor-а узла <tex>n'</tex>. Если <tex>n'</tex> ещё не выполняет условие планирования, A* будет неоднократно возобновляться пока механизм планирования не допустит алгоритму Дейкстры положить <tex>n'</tex> в поисковую очередь. Заметим, что таким образом не требуется каких-либо дополнительных усилий во время типичного поиска Дейкстры. | |
| − | + | Мы может быть уверены, что нерассмотренные узлы не будут принудительно опущены после применения операции heaping-up к <tex>n'</tex>. Иначе, мы могли бы иметь узел <tex>n''</tex>, который являлся бы ребенком n и впоследствии был бы заменен узлом <tex>n'</tex>. Заметим, что <tex>n''</tex> должен быть рассмотрен, поскольку <tex>n'</tex> был раскрыт. Однако, это противоречение к лемме 7, которая гарантирует, что этого не произойдет. | |
| − | |||
| − | + | Более того, следующее следствие гарантирует, что наилучшее <tex>d(n')</tex> не лучше, чем <tex>d</tex>-значение любой рассмотренной вершины, в частности, раскрытой вершины. Это означает, что мы не упустим возможность раскрыть <tex>n'</tex>. | |
| − | + | {{Лемма | |
| + | |about=следствие 3 | ||
| + | |statement=Пусть <tex>n</tex> будет узлом в <tex>P(G)</tex>, который был раскрыт Дейкстрой. Кроме того, пусть <tex>m</tex> будет узлом, который заново добавляется в <tex>P(G)</tex> или его позиция изменена, после того как <tex>n</tex> был раскрыт. Если <tex>h</tex> допустимая, тогда выполяется следующее: | ||
| + | <tex>C_{P(G)}(R,m) >= d(n)</tex> | ||
| + | |proof=... | ||
| + | }} | ||
| − | + | == 4.6 Пример == | |
| − | + | Мы проиллюстрируем работу алгоритма K* следующим примером. Мы будем рассматривать ориентированный взвешанный граф G на рисунке 7. Стартовой вершиной будет называться <tex>s_0</tex> и конечной вершиной - <tex>s_6</tex>. Нас интересует поиск 9 лучших путей из <tex>s_0</tex> в <tex>s_6</tex>. Для достижения этой цели мы применим алгоритм K* к <tex>G</tex>. Предположим, что эвристическая оценка существует. Значения эвристики даны в пометках c <tex>h(s_0)</tex> по <tex>h(s_6)</tex> на рисунке 7. Легко заметить, что эвристическая функция допустима. | |
| − | == | ||
| − | |||
| − | |||
| − | * | + | Первый раз A* делает итерации на графе <tex>G</tex> до тех пор, пока не будет найдена вершина <tex>s_6</tex>. Часть графа <tex>G</tex>, которая уже была рассмотрена иллиюстрируется на рисунке 8. Ребра, изображенные сплошными линиями, обозначают ребра дерева, в то время, как все остальные - запасные ребра. Они будет храниться в кучах <tex>H_{in}</tex>, показанных на рисунке 9. Номера, присвоенные узлах кучи, соответствуют <tex>\delta</tex>-значениям. На этом этапе поиска A* приостановлен и <tex>P(G)</tex> построен. Первоначально, только назначенный корень <tex>R</tex> явно доступен в <tex>P(G)</tex>. Инициализируется алгоритм Дейкстры. Это означает, что узел <tex>R</tex> добавляется в поискую очередь Дейкстры. Планировщику требуется доступ к successors К для того, чтобы решить следует ли возобновлять Дейкстру или A*. На данном этапе должна быть построена деревянная куча <tex>H_{T}(s_6)</tex>. Куча <tex>H_{T}(s_4)</tex> требуется для построения <tex>H_{T}(s_6)</tex>. Следовательно, строются деревянные кучи <tex>H_{T}(s_6)</tex>, <tex>H_{T}(s_4)</tex>, <tex>H_{T}(s_2)</tex> и <tex>H_{T}(s_0)</tex>. Результат показан на рисунке 10, где сплошные линии представляют кучные ребра и пунктирные линии показывают кросс-ребра. Во избежание путаницы на рисунке некоторые из ребер не полностью изображены. Мы указываем каждое из них, используя короткую стрелку с конретной целью. |
| − | + | После построения, как показано 10, планировщик проверяет только ребенка <tex>(s_4, s_2)</tex> узла <tex>R</tex> на предмет того, что <tex>g(s_6) + d(s_4,s_2) <= f(s_1)</tex>. Отметим, что <tex>s_1</tex> является головой поисковой очереди A*. Значение <tex>d(s_4,s_2)</tex> равно 2, т.е. <tex>g(s_6) + d(s_4,s_2) = 7 + 2 = 9 = f(s_1)</tex>. Следовательно, планировщик позволяет Дейкстре раскрыть <tex>R</tex> и вставить <tex>(s_4,s_2)</tex> в поисковую очередь. При раскрытии <tex>R</tex> находится первый путь из ответа. Он строится из пути <tex>P(G)</tex>, содержащего единственный узел <tex>R</tex>. Этот путь приводит к пустой последовательности запасных ребер. Напомним, что пустая последовательность запасных ребер соответствует пути из <tex>s_0</tex> в <tex>s_6</tex> в дереве поиска, а именно <tex>s_0s_2s_4s_6</tex> длиной 7. Затем поиск Дейкстры приостанавливается, потому что для successor-ов узла <tex>(s_4,s_2)</tex> не выполняется условие <tex>g(s_6)+d(n)<=f(s_1)</tex>. Следовательно, возобновляется A*. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Мы предполагаем, что условие раскрытия определено как раскрытие одной вершины для того, чтобы пример был простым и иллюстративным. Поэтому A* раскрывает <tex>s_1</tex> и останавливается. Исследованная часть <tex>G</tex> на текущем этапе показана на рисунке 11. Результат раскрытия приведет к обнаружению 2 новых запасных ребер <tex>(s_1,s_2)</tex> и <tex>(s_1,s_6)</tex>, которые будут добавлены в <tex>H_{in}(s_2)</tex> и <tex>H_{in}(s_6)</tex> соответственно. Обновленные кучи <tex>H_{in}(s_2)</tex> и <tex>H_{in}(s_6)</tex> представлены на рисунке 12. Другие кучи остаются неизменными, как на рисунке 9. Граф путей <tex>P(G)</tex> перестаивается, как показано на рисунке 13. Затем алгоритм Дейкстры возобновляется. Заметим, что поисковая очередь Дейкстры содержит только <tex>(s_4,s_2)</tex> с <tex>d = 2</tex> на этом моменте. Используя ручное выполнение мы можем легко увидеть, что Дейкстра будет выдавать в ответ пути, перечисленные в таблице 1. | |
Текущая версия на 13:39, 19 августа 2015
Также как и алгоритм Эппштейна, K* выполняет поиск пути на графе и использует граф путей . Граф путей ищется с помощью алгоритма Дейкстры для того, чтобы вычислить пути в виде последовательности запасных путей. Общий принцип работы алгоритма K* следующий:
1) K* применяет A* на графе вместо обратного алгоритма Дейкстры, который используется алгоритмом Эппштейна. 2) Мы запускаем A* на и Дейкстру на в поочередном порядке, который позволяет Дейкстре вычислить требуемые пути до заверешения полного поиска алгоритма A* на графе .
Содержание
4.1 Поиск A* на G
K* применяет A* к входному графу для того, чтобы построить дерево поиска . Заметим, что A*, также как и алгоритм Дейкстры, строит дерево поиска в процессе нахождения кратчайшего пути . Эти деревья формируются с помощью ссылок на родительские узлы, которые хранятся в том время, как A* производит итерации для того, чтобы восстановить путь , когда вершина ещё не найдена. Запасные ребра, открытые в процессе поиска A* на графе G, немедленно добавляются в граф P(G), структура которого будет объясняться в разделе 4.3.
В K* A* применяется к графу в прямом направлении в отличие от алгоритма Эппштейна, из-за чего корнем дерева является вершина начальная . Это необходимо для того, чтобы была возможность работать c неявным описанием графа через функцию successor (функция, возвращающая список исходящих ребер из данной вершины). На протяжение статьи будем считать граф конечным, если не будет сказано иное. Заметим, что А* корректен на конечных графах. Будем следовать литературному соглашению, предполагая, что стоимость бесконечного пути неограниченна.
4.2 Стоимость объезда
Для ребра стоимость объезда (англ. detour) представляет стоимость ущерба (англ. disadvantage) из-за взятия ребра объезда в сравнении с кратчайшим путем через . Ни длина кратчайшего пути через , ни длина пути , включающего запасные ребра не известны, когда A* обнаруживает . Обе длины могут быть оценены с помощью функции оценки , которая использует эвристическую функцию . Пусть будет -значением с соответствии с деревом поиска и будет -значением в соответствии с родителем u, т.е. . Тогда может быть определена так:
Заметим, что дает точную объездную метрику, поскольку оценочное -значение не появляется в определении функции .
4.3 Структура графа путей
Структура графа путей довольно сложная. В принципе, будет ориентированным графом, вершины которого соответствуют ребрам в исходном графе . Он будет организован как коллекция взаимосвязанных куч (англ. heap). 2 бинарные кучи минимума присвоены к каждой вершине в графе , которые называются входящей кучей (англ. incoming heap) и деревянной кучей (англ. tree heap) . Эти кучи являются базисом . Как мы покажем далее, использование этих куч также играет главную роль в поддержании асимптотической сложности K*, также как в EA и LVEA.
Входящая куча содержит узлы для каждого запасного ребра к вершине , которые до сих пор были обнаружены A*. Узлы будут упорядочены в соответствии с -значением соответствующих переходов. Узел владеющий ребром с минимальной стоимостью ущерба будет расположен на вершине кучи. Мы ограничим структуру кучи таким образом, что её корень в отличие от остальных узлов, будет иметь не более 1 ребенка. Обозначим его .
Пример 4. Рисунок 4 иллюстрирует входящие кучи графа из рисунка 3. Цифры рядом с узлами кучи соответствуют -значениям.
Деревянная куча для произвольной вершины строится следующим образом. Если - стартовая вершина, т.е. , то будет изначально пустой кучей. Затем в неё будет добавлен , если не пустая. Если не стартовая вершина, то пусть вершина будет родителем вершины в дереве поиска . Мы можем представить, что конструируется как копия , в которую добавлен . Если пустая, то идентична . Однако, для экономии памяти мы создаем только дешевую копию . Это осуществляется через создание копий только тех узлов кучи, которые лежат на обновленном пути в . Оставшаяся часть не копируется. Другими словами, вставляется в неразрушающим путем так, что структура сохраняется. В куче к могут быть присоединены 1 или 2 ребенка. К тому же, хранит только 1 собственного ребенка из . Мы обозначим корень как .
Назовем ребра, которые берут начало из входящих или деревянных куч, кучными ребрами (англ. heap edges). Сформулируем следующую лемму.
| Лемма (1): |
Все узлы, достижимые из по кучным ребрам, для каждой вершины формируют тернарную кучу, упорядоченную в соответствии с -значением. Мы назовем такую кучу графовой кучей (англ. graph heap) вершины и обозначим её как . |
| Доказательство: |
| Те узлы, которые находятся в или во входящей куче, на которую ссылается узел из , достижимы по кучным ребрам из . Деревянная куча формируется через добавление корней входящих куч всех вершин, лежащих на пути из стартовой вершины до в бинарной куче. Каждый из этих корней имеет максимум 3 детей: до 2 в и дополнительно единственного из входящей кучи. Любой другой узел, живущий во входящей куче имеет не больше 2 детей. Напомним, что каждая входящая куча - это бинарная куча с ограничением, что корень имеет единственного ребенка. Древовидная структура непосредственный результат древовидных структур и входящих куч. Более того, кучная характеристика деревянной кучи обеспечивает упорядочивание в соответствии с -значением по ребрам из , а кучная характеристика входящих куч - по всем ребрам из . Все это приводит к тому, что - тернарная куча, упорядоченная в соответствии с -значением. |
Финальная структура получется из входящих и деревянных куч следующим образом. К каждому узлу из , несущему ребро , мы присоединим указатель, ссылающийся на , который является корневым узлом . Мы назовем такие указатели кросс-ребрами (англ. cross edges), в то время как указатели, возникающие из куч названы кучными ребрами, как упоминалось раньше. Более того, мы добавим специальный узел в с одним выходящим кросс-ребром к .
Более того, мы определим весовую функцию на ребрах из . Пусть обозначает ребро в , и пусть и обозначают ребра из , соответствующие узлам и . Тогда определим следующим образом:
Лемма 1 подразумевает, что куча упорядоченная в соответствии с -значанием поддерживается для любого кучного ребра из . Эта упорядочивание кучи подразумевает, что неотрицательна для любого кучного ребра . Следовательно, также неотрицательна, т.е. для любого ребра в . Стоимость пути , т.е. равна .
Пример 6.
В оставшейся части этого раздела мы проиллюстрируем особенности структуры графа путей, которые актуальны для нахождения кратчайших путей .
Первое наблюдение в том, что ориентированный взвешенный граф. Каждый узел в несет запасное ребро из G. Использование бинарных куч в конструкции извлекает выгоду из следующих 2 свойств. Во-первых, произвольный узел в имеет не более 4 выходящих ребер. Одним из ребер будет точно кросс-ребро в то время, как оставшимися будут кучные ребра. Во-вторых, функция веса неотрицательна. Как станет ясно в разделе 5, эти свойства необходимы для доказательства правильности и определения сложности K*.
Второе наблюдение заключается в существовании соответствия один-к-одному между путей в и путей в , которые начинаются в .
...
| Лемма (2): |
Пусть будет узлом графовой кучи для какой-нибудь вершины . Пусть будет ребром связанным с . Тогда существует путь в дереве поиска из в . |
| Доказательство: |
| ... |
4.4 Алгоритмическая структура K*
Алгоритмический принцип K* следующий. Будем запускать алгоритмы Дейкстры и A* на с чередованием. Сначала, мы выполним A* на , который будет работать до тех, пока вершина не будет выбрана из очереди для раскрытия. Затем, вы запустим алгоритм Дейкстры на доступной части . Каждый узел раскрытый Дейкстрой представляет путь. Если точнее, то путь в , по которому Дейкстра достигла этого узла является решением. Путь может быть построен из за линейное время путем вычисления последовательности запасных ребер и затем пути из неё. Если Дейкстра находит кратчайших путей, то K* завершается успешно. Иначе, A* возобновляется для исследования большей части . Это приводит к росту , на котором алгоритм Дейкстры затем будет возобновлен. Мы будем повторять этот процесс до тех пор, пока алгоритм Дейкстры не найдет кратчайших путей.
Data: A graph given by its start vertex s ∈ V and its successor function succ and a natural number k Result: A list R containing k sidetrack edge sequences representing k solution paths
1 ← пустая приоритетная очередь 2 ← пустая хеш-таблица 3 ← пустой список 4 ← пустой граф путей 5 Выполняем A* на графе пока не будет выбрана для раскрытия 6 Если вершина не была достигнута, то выходим без ответа 7 Кладем в очередь 8 while A queue or open D is not empty: 9 if A queue is not empty: 10 if очередь не пуста: 11 Let u be the head of the search queue of A ∗ and n the head of 12 13 if (u) then переходим на строку 17. 14 Возобновляем A* для того, чтобы исследовать более большую часть графа 15 Обновляем and bring Dijkstra’s search into a consistent status 16 Переходим на строку 8 17 if очередь пуста: переходим на строку 8. 18 Remove from and place on the node n with the minimal d-value. 19 foreach referred by n in P(G): 20 21 Attach to a parent link referring to . 22 Insert n 0 into 23 Пусть будет путем в , через который узел n был достигнут. 24 Добавим в конец списка . 25 if : переходим на строку 26. 26 Return R and exit.
Алгоритм 1 содержит псевдокод K*. Код с 8 по 25 строчку образует главный цикл K*. Цикл завершается, когда очереди обоих алгоритмов А* и Дейкстры пусты. До 8 строчки выполняет некоторые подготовительные вещи. После инициализации, А* запускает на 5 строчке пока вершина не будет выбрана им для рассмотрения, в этом случае кратчайший путь будет найден. Если не достигнута, то алгоритм завершается без ответа. Отметим, что он не завершится на бесконечных графах. Иначе, алгоритм добавляет специальную вершину , которая назначена корнем , в поисковую очередь алгоритма Дейкстры. Затем, K* входит в главный цикл.
K* поддерживает механизм планирования для контролирования, когда A* или Дейкстра будет возобновлены. Если очередь из A* не пуста, что означает, что А* ещё не завершил исследования всего графа G, то Дейкстра возобновляется тогда и только тогда, когда . Значение является максимальным -значением среди всех successor-ов головы поисковой очереди алгоритма Дейкстры. Вершина является головой поисковой очереди A*. Напомним, что - функция расстояния, используемая в алгоритме Дейкстры. Если очередь поиска Дейкстры пуста или , то А* возобновляется для того, чтобы исследовать более большую часть графа (строка 14). То, как долго мы ему позволим работать, является компромиссом. Если мы запустим его только на маленьком количестве шагов, то мы дадим Дейкстре шанс найти необходимое количество путей скорее, чем они будут доступны в . С другой стороны, мы вызываем накладные расходы путем переключения A* и Дейкстры и поэтому должны ограничить количество переключений. Эти накладные расходы вызваны тем фактом, что после возобновления A* (строка 14), структура графа может измениться. Следовательно нам необходимо обновить (строка 15), как мы будет широко обсуждать в разделе 4.5. Это требует последующую проверку статуса Дейкстры. Мы должны быть уверены, что Дейкстра поддерживает согласованное состояние после изменений в . K* предусматривает условие, которые управляет решением, когда остановить A*, которое мы назовем условие расширения. Для того, чтобы поддерживать аналогичную асимптотическую сложность как у EA и LVEA, мы должны определить условие расширения так, чтобы A* выполнялся пока количество рассмотренных вершин и количество внутренних ребер удваивается или полностью исследован. Мы обсудим эту проблему несколько подробнее позже. В качестве полезного свойства, K* позволяет другое определения этого условия, которое может быть более эффективным на практике. В наших экспериментах в разделе 6, мы определили условие расширения так, что количество рассмотренных вершин или количество рассмотренных ребер ребер возрастает на 20% при каждом запуске A*. Этот механизм планирования включен до тех пор, пока A* не закончит исследовать весь граф . Как только A* исследует весь граф (строка 9), механизм планирования отключается и в дальнейшем работает только алгоритм Дейкстры.
Строки 18-22 представляют обычный шаг рассмотрения узла алгоритмом Дейкстры. Отметим, что когда successor-узел сгенерирован, K* не проверяет был ли уже посещен до этого. Другими словами, каждый раз, когда узел генерируется, он рассматривает как новый. Эта стратегия обоснована на наблюдении, что путь s-t может содержать одно и то же ребро несколько раз. Строка 24 добавляет следующий путь в результирующее множество R. Это делается путем конструирования последовательности запасных ребер из пути , через которые Дейкстра достигла узла , который был только что рассмотрен. Алгоритм завершается, когда в результирующее множество добавлено последовательностей запасных ребер (строка 25).
4.5 Взаимосвязь алгоритмов Дейкстры и A*
Тот факт, что оба алгоритма A* и Дейкстры делят между собой граф путей , вызывает обеспокоенность в отношении правильности работы Дейкстры на . Возобновление A* приводит к изменениям в структуре . Таким образом, после возобновления A*, мы обновляем и проверяет статус поиска Дейкстры (строка 15). В основном, A* может добавить новые узлы, менять -значения существующих узлов или даже удалять узлы. A* может также существенно изменять дерево поиска , которое будет в худшем случае разрушать структуру все деревянных куч . Эти изменения могут приводить к глобальной реструктуризации или даже перестроению с нуля. В худшем случае это может сделать предыдущие поиски Дейкстры на бесполезными таким образом, что нам придется перезапускать алгоритм Дейкстры с нуля.
Если использованная эвристическая оценка допустимая, то наше положение лучше. Нам по-прежнему может понадобится перестроение , но мы покажем, что это перестроение не мешает корректности поиска Дейкстры на . Другими словами, мы не теряем результаты, до сих пор полученные поиском Дейкстры.
В случае монотонной эвристической оценки мы даже не нуждаемся в восстановлении или перестроении . Если монотонная, то дерево поиска A* является деревом кратчайшего пути для всех раскрытых вершин. Следовательно, g-значения раскрытых вершин не меняются. Это означает, что -значения для внутренних ребер никогда не изменятся. Ребра дерева раскрытых вершин не изменятся также. Следовательно, обновление -значений, heaping-up, heaping-down (операции в кучах) или удаление узлов не влекут за собой каких-либо изменений в . Только добавление новых узлов приводит к изменениям в . Следовательно, восстановление или глобальное перестроение не требуется в данном случае.
В оставшейся части этого раздела, мы сначала покажем, что корректность поиска Дейкстры на поддерживается в случае допустимой эвристической оценки. После этого мы покажем, что изменения в могут помешать завершенности поиска Дейкстры независимо от того, является ли эвристика допустимой или даже монотонной. Следовательно, мы предложим механизм для её поддержания.
Мы фокусируемся дальше на корректности поиска Дейкстры на в случае допустимой эвристической оценки. Сначала, мы заявляем, что если допустимая, то узлы исследованной части не поменяют свои -значения.
| Лемма (6): |
Пусть будет произвольным узлов в и пусть будет ребром, связанным с . Если допустимая функция, то значение никогда не изменится после того, как будет рассмотрен алгоритмом Дейкстры. |
| Доказательство: |
| ... |
Из леммы 6 мы может вывести следующее следствие.
| Лемма (следствие 3): |
Пусть будет произвольным узлом в . Если допустимая функция, то никогда не будет удален из после того, как был рассмотрен алгоритмом Дейкстры. |
| Доказательство: |
| ... |
Более того, мы докажем, что структура исследованной части не изменится.
| Лемма (7): |
Пусть будет произвольным узлов в . Если допустимая функция, то никогда не изменит свою позицию после того, как он был рассмотрен алгоритмом Дейкстры. |
| Доказательство: |
| ... |
Леммы 6 и 7 обеспечивают, что изменения в , которые индуцируются A*, не влияют на часть , которую алгоритм Дейкстры уже исследовал. Это гарантирует корректность поиска Дейкстры на , если используемая эвристика допустимая. Таким образом, каждый путь, который предоставляет алгоритм Дейкстры корректен и его длина действительна. Однако, это не обеспечивает завершенность поиска Дейкстры на .
Возможно, что узел присоединяется к другом узлу n как ребенок, после раскрытия узла . В этом случае братья будут рассотрены до того, как станет ребенком n. Поэтому мы должны рассмотреть то, что было упущено во время поиска в связи с отсутствием . Мы добиваемся этого путем применения строк 20-22 к для каждого раскрытого направленного predecessor-а узла . Если ещё не выполняет условие планирования, A* будет неоднократно возобновляться пока механизм планирования не допустит алгоритму Дейкстры положить в поисковую очередь. Заметим, что таким образом не требуется каких-либо дополнительных усилий во время типичного поиска Дейкстры.
Мы может быть уверены, что нерассмотренные узлы не будут принудительно опущены после применения операции heaping-up к . Иначе, мы могли бы иметь узел , который являлся бы ребенком n и впоследствии был бы заменен узлом . Заметим, что должен быть рассмотрен, поскольку был раскрыт. Однако, это противоречение к лемме 7, которая гарантирует, что этого не произойдет.
Более того, следующее следствие гарантирует, что наилучшее не лучше, чем -значение любой рассмотренной вершины, в частности, раскрытой вершины. Это означает, что мы не упустим возможность раскрыть .
| Лемма (следствие 3): |
Пусть будет узлом в , который был раскрыт Дейкстрой. Кроме того, пусть будет узлом, который заново добавляется в или его позиция изменена, после того как был раскрыт. Если допустимая, тогда выполяется следующее:
|
| Доказательство: |
| ... |
4.6 Пример
Мы проиллюстрируем работу алгоритма K* следующим примером. Мы будем рассматривать ориентированный взвешанный граф G на рисунке 7. Стартовой вершиной будет называться и конечной вершиной - . Нас интересует поиск 9 лучших путей из в . Для достижения этой цели мы применим алгоритм K* к . Предположим, что эвристическая оценка существует. Значения эвристики даны в пометках c по на рисунке 7. Легко заметить, что эвристическая функция допустима.
Первый раз A* делает итерации на графе до тех пор, пока не будет найдена вершина . Часть графа , которая уже была рассмотрена иллиюстрируется на рисунке 8. Ребра, изображенные сплошными линиями, обозначают ребра дерева, в то время, как все остальные - запасные ребра. Они будет храниться в кучах , показанных на рисунке 9. Номера, присвоенные узлах кучи, соответствуют -значениям. На этом этапе поиска A* приостановлен и построен. Первоначально, только назначенный корень явно доступен в . Инициализируется алгоритм Дейкстры. Это означает, что узел добавляется в поискую очередь Дейкстры. Планировщику требуется доступ к successors К для того, чтобы решить следует ли возобновлять Дейкстру или A*. На данном этапе должна быть построена деревянная куча . Куча требуется для построения . Следовательно, строются деревянные кучи , , и . Результат показан на рисунке 10, где сплошные линии представляют кучные ребра и пунктирные линии показывают кросс-ребра. Во избежание путаницы на рисунке некоторые из ребер не полностью изображены. Мы указываем каждое из них, используя короткую стрелку с конретной целью.
После построения, как показано 10, планировщик проверяет только ребенка узла на предмет того, что . Отметим, что является головой поисковой очереди A*. Значение равно 2, т.е. . Следовательно, планировщик позволяет Дейкстре раскрыть и вставить в поисковую очередь. При раскрытии находится первый путь из ответа. Он строится из пути , содержащего единственный узел . Этот путь приводит к пустой последовательности запасных ребер. Напомним, что пустая последовательность запасных ребер соответствует пути из в в дереве поиска, а именно длиной 7. Затем поиск Дейкстры приостанавливается, потому что для successor-ов узла не выполняется условие . Следовательно, возобновляется A*.
Мы предполагаем, что условие раскрытия определено как раскрытие одной вершины для того, чтобы пример был простым и иллюстративным. Поэтому A* раскрывает и останавливается. Исследованная часть на текущем этапе показана на рисунке 11. Результат раскрытия приведет к обнаружению 2 новых запасных ребер и , которые будут добавлены в и соответственно. Обновленные кучи и представлены на рисунке 12. Другие кучи остаются неизменными, как на рисунке 9. Граф путей перестаивается, как показано на рисунке 13. Затем алгоритм Дейкстры возобновляется. Заметим, что поисковая очередь Дейкстры содержит только с на этом моменте. Используя ручное выполнение мы можем легко увидеть, что Дейкстра будет выдавать в ответ пути, перечисленные в таблице 1.