Формула Эйлера

Теорема (Формула Эйлера):

Для произвольного плоского связного графа [math]G[/math] с [math]V[/math] вершинами, [math]E[/math] ребрами и [math]F[/math] гранями справедливо следующее соотношение: [math]V - E + F = 2[/math]

Доказательство:

[math]\triangleright[/math]

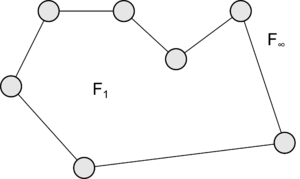
Воспользуемся методом математической индукции по количеству граней графа. База индукции: [math]F = 2[/math]. Граф [math]G[/math] представляет собой многоугольник с [math]n[/math] вершинами (рис. 1). Тогда [math]V = E = n[/math], значит, равенство [math]V - E + F = 2[/math] выполняется. Индукционный переход: Покажем, что если теорема верна для графов с [math]F[/math] гранями, то она будет верна и для графов с [math]F + 1[/math] гранями. Пусть [math]G[/math] - плоский граф, имеющий [math]V[/math] вершин, [math]E[/math] ребер и [math]F[/math] граней, и для него справедлива формула Эйлера. Добавим новую грань (пунктирная линия на рис.2), проводя по внешней грани [math]F_{\infty}[/math] некоторую элементарную цепь, соединяющую две вершины максимального цикла графа [math]G[/math]. Если эта цепь имеет [math]r[/math] ребер, то необходимо добавить [math]r - 1[/math] новых вершин и одну новую грань. Ясно, что формула Эйлера останется справедливой и для нового графа, так как [math]V' - E' + F' = (V + r - 1) - (E + r) + (F + 1) = V - E + F[/math]

[math]\triangleleft[/math]

рис. 1

рис. 2

Теорема (Следствие из формулы Эйлера):

Пусть [math]G[/math] связный планарный обыкновенный граф с [math]V[/math] вершинами ([math]V \ge 3[/math]), [math]E[/math] ребрами и [math]F[/math] гранями. Тогда [math]E \le 3V - 6[/math]

Доказательство:

[math]\triangleright[/math]

Поскольку [math]G[/math] не содержит петель и кратных ребер, то каждая грань граничит хотя бы с тремя ребрами. Пусть, двигаясь вдоль [math]i[/math]-й грани мы пройдем [math]l_i[/math] ребер. Очевидно, что [math]\sum \limits_{i=1}^{F}l_i = 2E[/math]. Поскольку [math]l_i \ge 3 \hspace{3pt} (i = 1..F)[/math], получаем [math]3F \le 2E[/math]. Из формулы Эйлера [math]3E - 3V + 6 = 3F \le 2E[/math], то есть [math]E \le 3V - 6[/math].

[math]\triangleleft[/math]

Определение:

Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников.

Определение:

Фигура Ф называется выпуклой, если любые две ее точки можно соединить отрезком, целиком содержащейся в этой фигуре.

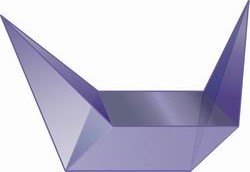
Пример невыпуклого многоугольника

Утверждение:

Все грани выпуклого многогранника являются выпуклыми многоугольниками.

Теорема (Формула Эйлера для многогранников):

Для любого выпуклого многогранника имеет место равенство [math]V - E + F = 2[/math], где [math]V[/math] - число вершин, [math]E[/math] - число ребер и [math]F[/math] - число граней данного многогранника.

Доказательство:

[math]\triangleright[/math]

Для доказательства соотношения Эйлера представим поверхность выпуклого многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим сетку, содержащую [math]F' = F - 1[/math] многоугольников (которые, по-прежнему, будем называть гранями), [math]V[/math] вершин и [math]E[/math] ребер. Для этой сетки справедливо соотношение [math]V - E + F ' = 1 [/math]. Подставляем [math]F' = F - 1[/math] и получаем [math]V - E + F = 2[/math].

[math]\triangleleft[/math]

Теорема (Следствие из формулы Эйлера для многогранников):

В любом выпуклом многограннике имеется или треугольная грань, или трехгранный угол. Более того, число треугольных граней плюс число трехгранных углов больше или равно восьми.

Доказательство:

[math]\triangleright[/math]

Обозначим через [math]V_{i}[/math] число вершин выпуклого многогранника, в которых сходится [math]i[/math] ребер. Тогда для общего числа вершин [math]V[/math] имеет место равенство [math]V = V_{3} + V_{4} + V_{5} + \dots[/math]. Аналогично, обозначим через [math]F_{i}[/math] число граней выпуклого многогранника, у которых имеется [math]i[/math] ребер. Тогда для общего числа граней [math]F[/math] имеет место равенство [math]F = F_{3} + F_{4} + F_{5} + \dots[/math] . Посчитаем число ребер [math]E[/math] многогранника. Имеем: [math]3V_{3} + 4V_{4} + 5V_{5} + \dots = 2E[/math], [math]3F_{3} + 4F_{4} + 5F_{5} + \dots = 2E[/math]. По теореме Эйлера выполняется равенство [math]4V – 4E + 4F = 8[/math]. Подставляя вместо [math]V[/math], [math]E[/math] и [math]F[/math] их выражения, получим: [math]4V_{3} + 4V_{4} + 4V_{5} + \dots – (3V_{3} + 4V_{4} + 5V_{5} + \dots) - (3F_{3} + 4F_{4} + 5F_{5} + \dots) + 4F_{3} + 4F_{4} + 4F_{5} + \dots = 8[/math]. Следовательно, [math]V_{3} + F_{3} = 8 + V_{5} + \dots + F_{5} + \dots [/math], значит, число треугольных граней плюс число трехгранных углов больше или равно восьми.

[math]\triangleleft[/math]

Литература

• Асанов М,, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы
• О.Оре - Графы и их применение