Generative Adversarial Nets (GAN) — различия между версиями
Imka239 (обсуждение | вклад) (→CGAN (Conditional Generative Adversarial Nets)) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 105 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[File:Арх_ган.png|450px|thumb|Оригинальная архитектура GAN]] | + | [[File:Арх_ган.png|450px|thumb|Рисунок 1. Оригинальная архитектура GAN]] |
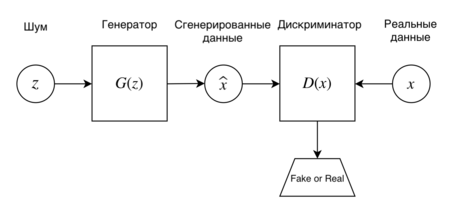
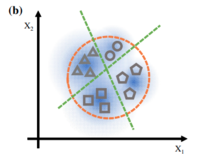
| − | '''Порождающие состязательные сети''' (англ. ''Generative Adversarial Nets, GAN'') {{---}} алгоритм машинного обучения, входящий в семейство [[:Порождающие модели|порождающих моделей]] и построенный на комбинации из двух нейронных сетей: генеративная модель <tex>G</tex>, которая строит приближение распределения данных, и дискриминативная модель <tex>D</tex>, оценивающая вероятность, что образец пришел из тренировочных данных, а не сгенерированных моделью <tex>G</tex>. Обучение для модели <tex>G</tex> заключается в максимизации вероятности ошибки дискрминатора <tex>D</tex>. Впервые такие сети были представлены Иэном Гудфеллоу в 2014 году. | + | '''Порождающие состязательные сети''' (англ. ''Generative Adversarial Nets, GAN'') {{---}} алгоритм машинного обучения, входящий в семейство [[:Порождающие модели|порождающих моделей]] и построенный на комбинации из двух нейронных сетей: генеративная модель <tex>G</tex>, которая строит приближение распределения данных, и дискриминативная модель <tex>D</tex>, оценивающая вероятность, что образец пришел из тренировочных данных, а не сгенерированных моделью <tex>G</tex> (рис. 1). Обучение для модели <tex>G</tex> заключается в максимизации вероятности ошибки дискрминатора <tex>D</tex>. Впервые такие сети были представлены Иэном Гудфеллоу в 2014 году. |
==Постановка задачи и метод== | ==Постановка задачи и метод== | ||
| Строка 10: | Строка 10: | ||
==Интуитивный процесс тренировки== | ==Интуитивный процесс тренировки== | ||
| − | [[File:GANIntuitive.jpg|500px|thumb|right|Иллюстрация процесса тренировки порождающих состязательных сетей GAN. Источник: https://arxiv.org/pdf/1701.07875.pdf]] | + | [[File:GANIntuitive.jpg|500px|thumb|right|Рисунок 2. Иллюстрация процесса тренировки порождающих состязательных сетей GAN. Источник: https://arxiv.org/pdf/1701.07875.pdf]] |
| − | + | Как показано на рисунке 2, генеративные состязательные сети обучаются путем одновременного обновления дискриминирующего распределения (<tex>D</tex> синяя пунктирная линия), так чтобы дискриминатор мог различать объекты из распределения тренировочного сета(черная пунктирная в точку линия) и из распределения генератора (<tex>G</tex> зеленая сплошная линия). Нижняя горизонтальная линия представляет собой область, из которой составлена выборка <tex>z</tex>, в нашем случае равномерно. Горизонтальная линия над ней является частью области <tex>x</tex>. Стрелками на картинке показано, как отображение <tex>x = G(z)</tex>, накладывает неравномерное распределение <tex>p_{g}</tex> на тренировочное. <tex>G</tex> сжимается в областях с высокой плотностью и расширяется в областях с низкой. | |
| − | Рассмотрим описанный на картинках процесс. (a) Близкая сходимость состязающейся пары: <tex>p_{g}</tex> похоже на распределение <tex>p_{data} и D</tex> частично-точный классификатор. (b) Во внутреннем цикле алгоритма <tex>D</tex> обучается отличать объекты из тренировочных данных, сходясь к <tex>\frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}</tex>. (c) После обновления <tex>G</tex> градиент <tex>D</tex> привел <tex>G(z)</tex> к передвижению в область, с большей вероятностью быть классифицированным как данные. (d) После нескольких шагов обучения <tex>G</tex> и <tex>D</tex> придут в состояние, в котором не смогу улучшиться, так как будет выполняться условие <tex>p_{g} = p_{data}</tex> и | + | Рассмотрим описанный на картинках процесс. (a) Близкая сходимость состязающейся пары: <tex>p_{g}</tex> похоже на распределение <tex>p_{data} и D</tex> частично-точный классификатор. (b) Во внутреннем цикле алгоритма <tex>D</tex> обучается отличать объекты из тренировочных данных, сходясь к <tex>\frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}</tex>. (c) После обновления <tex>G</tex> градиент <tex>D</tex> привел <tex>G(z)</tex> к передвижению в область, с большей вероятностью быть классифицированным как данные. (d) После нескольких шагов обучения <tex>G</tex> и <tex>D</tex> придут в состояние, в котором не смогу улучшиться, так как будет выполняться условие <tex>p_{g} = p_{data}</tex> и дискриминатор не сможет различать два распределения и его выход всегда будет <tex>D(x) = \frac{1}{2}</tex>. |
==Оригинальный алгоритм обучения GAN== | ==Оригинальный алгоритм обучения GAN== | ||
| − | [[File:Обучение_ган.png|450px|thumb|right|Визуализация генерирования фотографии с помощью DCGAN по одному и тому же шуму в зависимости от итерации обучения. Источник: https://arxiv.org/pdf/1701.07875.pdf]] | + | [[File:Обучение_ган.png|450px|thumb|right|Рисунок 3. Визуализация генерирования фотографии с помощью DCGAN по одному и тому же шуму в зависимости от итерации обучения. Источник: https://arxiv.org/pdf/1701.07875.pdf]] |
В процессе обучения требуется делать два шага оптимизации поочередно: сначала обновлять веса генератора <tex>\gamma_{g}</tex> при фиксированном <tex>\gamma_{d}</tex>, а затем веса дискриминатора <tex>\gamma_{d}</tex> при фиксированном <tex>\gamma_{g}</tex>. На практике дискриминатор обновляется <tex>k</tex> раз вместо одного, поскольку, полностью оптимизировать дискриминатор вычислительно не выгодно и на конечных сетах он может переобучиться. Таким образом <tex>k</tex> является гиперпараметром. | В процессе обучения требуется делать два шага оптимизации поочередно: сначала обновлять веса генератора <tex>\gamma_{g}</tex> при фиксированном <tex>\gamma_{d}</tex>, а затем веса дискриминатора <tex>\gamma_{d}</tex> при фиксированном <tex>\gamma_{g}</tex>. На практике дискриминатор обновляется <tex>k</tex> раз вместо одного, поскольку, полностью оптимизировать дискриминатор вычислительно не выгодно и на конечных сетах он может переобучиться. Таким образом <tex>k</tex> является гиперпараметром. | ||
| Строка 35: | Строка 35: | ||
<tex>g_w \leftarrow \mathop{\nabla}_{\gamma_{g}} { \frac{1}{m} \sum_{t = 1}^m \limits} [log(1-D(G(z_t))] </tex> | <tex>g_w \leftarrow \mathop{\nabla}_{\gamma_{g}} { \frac{1}{m} \sum_{t = 1}^m \limits} [log(1-D(G(z_t))] </tex> | ||
'''end''' '''for''' | '''end''' '''for''' | ||
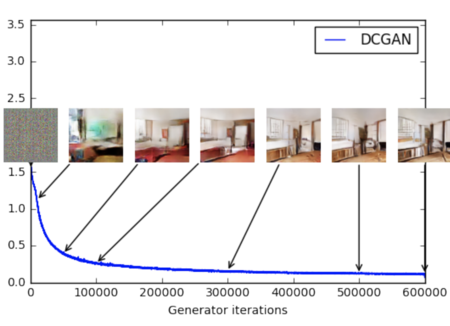
| − | На практике не всегда удобно использовать уравнение описанной выше. В начале обучения, когда <tex>G</tex> плохо настроен дискриминатор <tex>D</tex> может не учитывать объекты, с высокой уверенностью в классификации, так как они сильно отличаются от | + | На практике не всегда удобно использовать уравнение описанной выше. В начале обучения, когда <tex>G</tex> плохо настроен дискриминатор <tex>D</tex> может не учитывать объекты, с высокой уверенностью в классификации, так как они сильно отличаются от тренировочного сета, в таком случае <tex>log(1 - D(G(z)))</tex> стагнирует. Чтобы избежать этого, можно вместо минимизации <tex>log(1 - D(G(z)))</tex> максимизировать <tex>log D(G(z))</tex>. На рисунке 3 представлена зависимость получаемого изображения от итерации обучения. |
| − | == | + | ==Проблемы обучения GAN== |
Большинство GAN'ов подвержено следующим проблемам: | Большинство GAN'ов подвержено следующим проблемам: | ||
| − | + | * Схлопывание мод распределения (англ. mode collapse): генератор коллапсирует, то есть выдает ограниченное количество разных образцов. | |
| − | * Схлопывание мод распределения (mode collapse): генератор коллапсирует, | + | * Проблема стабильности обучения (англ. non-convergence): параметры модели дестабилизируются и не сходятся. |
| − | * Исчезающий градиент (diminished gradient): дискриминатор становится слишком "сильным", а градиент генератора исчезает и обучение не происходит | + | * Исчезающий градиент (англ. diminished gradient): дискриминатор становится слишком "сильным", а градиент генератора исчезает и обучение не происходит. |
| + | * Проблема запутывания (англ. disentanglement problem): выявление корреляции в признаках, не связанных (слабо связанных) в реальном мире. | ||
* Высокая чувствительность к гиперпараметрам. | * Высокая чувствительность к гиперпараметрам. | ||
| − | + | Часть этих проблем будет рассмотрена подробнее ниже, но нужно заметить, что универсального подхода к решению большинства из них нет. Зато существуют практические советы<ref> [https://github.com/soumith/ganhacks How to Train a GAN? Tips and tricks to make GANs work]</ref>, которые могут помочь при обучении GAN'ов. Основными из них являются: | |
# Нормализация данных. Все признаки в диапазоне $[-1; 1]$; | # Нормализация данных. Все признаки в диапазоне $[-1; 1]$; | ||
# Замена функции ошибки для $G$ с $\min log (1-D)$ на $\max log D$, потому что исходный вариант имеет маленький градиент на раннем этапе обучения и большой градиент при сходимости, а предложенный наоборот; | # Замена функции ошибки для $G$ с $\min log (1-D)$ на $\max log D$, потому что исходный вариант имеет маленький градиент на раннем этапе обучения и большой градиент при сходимости, а предложенный наоборот; | ||
# Сэмплирование из многомерного нормального распределения вместо равномерного; | # Сэмплирование из многомерного нормального распределения вместо равномерного; | ||
# Использовать нормализационные слои (например, batch normalization или layer normalization) в $G$ и $D$; | # Использовать нормализационные слои (например, batch normalization или layer normalization) в $G$ и $D$; | ||
| − | # Использовать метки для данных, если они имеются, | + | # Использовать метки для данных, если они имеются, то есть обучать дискриминатор еще и классифицировать образцы. |
| + | |||
| + | ===Коллапс мод=== | ||
| + | |||
| + | [[File:mode_collapse.png|600px|thumb|right|Рисунок 4. Проблема mode collapse в GAN сетях, на нижнем ряду представлен обычный GAN, на верхнем {{---}} UGAN с 10 обратными шагами (англ. unrolled steps). Источник: https://arxiv.org/pdf/1611.02163.pdf]] | ||
| + | |||
| + | [[File:mode_collapse_UGAN.png|600px|thumb|right|Рисунок 5. Проблема mode collapse в GAN сетях на примере MNIST датасета, на нижнем ряду представлен обычный GAN, на верхнем {{---}} UGAN с 20 обратными шагами (англ. unrolled steps). Источник: https://arxiv.org/pdf/1611.02163.pdf]] | ||
| + | |||
| + | В процессе обучения генератор может прийти к состоянию, при котором он будет всегда выдавать ограниченный набор выходов. При этом пространство, в котором распределены сгенерированные изображения, окажется существенно меньше, чем пространство исходных изображений. | ||
| + | Главная причина этого в том, что генератор обучается обманывать дискриминатор, а не воспроизводить исходное распределение. | ||
| + | Если генератор начинает каждый раз выдавать похожий выход, который является максимально правдоподобным для текущего дискриминатора, то зависимость от $z$ падает, а следовательно и градиент $G(z)$ стремиться к 0. Лучшей стратегией для дискриминатора будет улучшение детектирования этого конкретного изображения. | ||
| + | Так на следующих итерациях наиболее вероятно, что генератор придет к другому изображению, хорошо обманывающему текущий дискриминатор, а дискриминатор будет учиться отличать конкретно это новое изображение. Этот процесс не будет сходиться и количество представленных мод не будет расти, поэтому приблизиться к исходному распределению не удастся. На рисунке 4 наглядно представлена проблема mode collapse и то как генератор "путешествует" по модам не приближаясь к целевому распределению. | ||
| + | На рисунке 5 наглядно представлен пример mode collapse в процессе работы обычной GAN, обучаемой на датасете MNIST. | ||
| + | |||
| + | На текущий момент mode collape является одной из главных проблем GAN, эффективное решение которой ещё ищется. | ||
| + | Возможные решения проблемы mode collapse: | ||
| + | * WGAN {{---}} использование метрики Вассерштейна (англ. Wasserstein Loss) внутри функции ошибки, позволяет дискриминатору быстрее обучаться выявлять повторяющиеся выходы, на которых стабилизируется генератор<ref>[https://developers.google.com/machine-learning/gan/problems Common Problems]</ref>. | ||
| + | * UGAN (Unrolled GAN) {{---}} для генератора используется функция потерь, которая не только от того, как текущий дискриминатор оценивает выходы генератора, но и от выходов будущих версий дискриминатора. | ||
| + | |||
| + | ===Проблема стабильности обучения=== | ||
| + | |||
| + | [[File:Unstable_X_Y.png|600px|thumb|right|Рисунок 6. Симуляция изменения $x$ и $y$ с помощью градиентного спуска, где изменяя $x$ мы пытается минимизировать величину $x*y$, а при изменении $y$, наоборот, стараемся ее максимизировать. Шаг градиентного спуска <tex>\alpha = 0.1</tex>. Источник: https://lilianweng.github.io/lil-log/2017/08/20/from-GAN-to-WGAN.html]] | ||
| + | |||
| + | Задача обучения дискриминатора и генератора в общем смысле не является задачей поиска локального или глобального минимума функции, а является задачей поиска точки равновесия двух игроков. В теории игр эта точка называется точкой равновесия Нэша (англ. Nash equilibrium) в которой оба игрока больше не получают выгоды, хотя следуют оптимальной стратегии. | ||
| + | Рассмотрим задачу поиска этой точки на игрушечном примере, где $G$ хочет максимизировать произведение $xy$ а $D$ {{---}} минимизировать. Будем обновлять параметры $x$ и $y$ на основе градиентного спуска: | ||
| + | <tex> \Delta x = \alpha\frac{\delta(x*y)}{ \delta(x)} </tex> | ||
| + | <tex> \Delta y = - \alpha\frac{\delta(x*y)}{ \delta(y)} </tex> | ||
| + | Если изобразить на графике поведение $x$,$y$ и $xy$ (рис. 6) то станет ясно, что они не сойдутся, а амплитуда их движения будет только увеличиваться. | ||
| + | |||
| + | В оригинальной статье про GAN используется дивергенция Дженсена-Шеннона (англ. Jensen–Shannon divergence), которая в свою очередь использует дивергенцию Кульбака-Лейблера (англ. Kullback-Leibler divergence): | ||
| + | :<math>D_\text{KL}(P \parallel Q) = \int_{-\infty}^\infty p(x) \log\left(\frac{p(x)}{q(x)}\right)\, dx</math>, | ||
| + | где $P$ и $Q$ {{---}} $k$-мерные абсолютно непрерывные распределения, $p(x)$ и $q(x)$ {{---}} функции плотности этих распределений, заданные на <math>X \subseteq R^k</math>. | ||
| + | Нетрудно заметить, что при наличии $x$, в которых $q(x)=0$, весь интеграл разойдется, что плохо влияет на сходимость обучения. | ||
| + | |||
| + | Возможные решения проблемы стабильности: | ||
| + | *Регуляризация {{---}} Добавление шума ко входам дискриминатора и соответствующая настройка гиперпараметров дискриминатора. | ||
| + | *PGGAN (Progressive Growing of GANs, разработана NVidia<ref>[https://research.nvidia.com/sites/default/files/pubs/2017-10_Progressive-Growing-of/karras2018iclr-paper.pdf PROGRESSIVE GROWING OF GANS FOR IMPROVED | ||
| + | QUALITY, STABILITY, AND VARIATION]</ref>) {{---}} в процессе работы разрешение изображений увеличивается от очень малых (4 на 4 пикселя), до конечных (1024 на 1024 пикселя), что позволяет тренировать сначала выявление крупных черт а затем более мелких, что крайне положительно сказывается на стабильности. | ||
| + | *WGAN {{---}} В качестве функции дивергенции используется метрика Вассерштейна, которая в большинстве случаев решает проблему расходимости интеграла в функции Дженсена-Шеннона. | ||
| + | |||
| + | ===Проблема запутывания (Проблема связанности характеристик)=== | ||
| + | |||
| + | Сложность с генеративными состязательными сетями заключается в том, что непонятно, как им удается определять конкретные различные характеристики (возраст и пол, например) и связаны ли между собой эти характеристики. | ||
| + | |||
| + | Генератор хорошо обученной сети $-$ функция | ||
| + | <tex>g : Z \rightarrow X</tex>, где <tex>Z \subseteq \mathbb{R}^{d}</tex> $-$ скрытое пространство размерности <tex>d</tex>, для которого обычно применимо Гауссово распределение в многомерном случае. | ||
| + | <tex>X</tex> $-$ пространство изображений, где у каждого изображения существует набор характеристик вроде возраста или пола. Пусть нам дана функция оценки <tex>f_{S} : X \rightarrow S</tex>, где <tex>S \subseteq \mathbb{R}^{m}</tex> $-$ пространство изображений размерности <tex>m</tex>. Тогда <tex>s = f_{S}(g(z))</tex>, где <tex>z \in Z</tex>, <tex>s \in S</tex> $-$ связь между точкой в скрытом подпространстве и характеристиками получившегося изображения. Для функции оценок часто используют Inception score<ref>[https://arxiv.org/abs/1801.01973 Shane Barratt, Rishi Sharma {{---}} A Note on the Inception Score]</ref> и FID (Frechet Inception distance<ref> [https://en.wikipedia.org/wiki/Fr%C3%A9chet_inception_distance#:~:text=The%20Fr%C3%A9chet%20inception%20distance%20(FID,generative%20adversarial%20network%20(GAN). Frechet Inception distance on Wikipedia]</ref>), где главными критериями хорошо сгенерированных образцов является разнообразие отличительных черт в образцах и их выраженность. | ||
| + | |||
| + | Установлено, что при движении между двумя точками <tex>z_1</tex> и <tex>z_2</tex> характеристики меняются постепенно, без скачков. Тогда по этому направлению в $Z$ можно построить гиперплоскость. | ||
| + | Тогда сделаем предположение, при котором для любого бинарного параметра существует гиперплоскость, что все образцы с одной стороны от нее имеют одинаковое значение этого параметра. | ||
| + | |||
| + | Заведем следующую функцию "расстояния": <tex>d(n, z) = n^{T}z</tex>, где <tex>n \in \mathbb{R}^{d}</tex>, <tex>n</tex> $-$ вектор нормали гиперплоскости. | ||
| + | Данная функция не подходит под определение расстояния из-за наличия отрицательных значений (но знак нам необходим для определения знака параметра характеристики). | ||
| + | Ожидается, что есть близкая к линеной зависимость оценки $f$ по данному параметру от "расстояния": | ||
| + | |||
| + | <tex>f(g(z)) = \lambda d(n, z)</tex>. | ||
| + | |||
| + | [[File:SubspaceManipulation.png|200px|thumb|right|Рисунок 7. Манипулирование подпространством. Источник:<tex>\href{https://arxiv.org/pdf/1907.10786.pdf}{\text{[x]}}</tex>]] | ||
| + | В таком случае выраженность характеристики зависит от "расстояния" до этой гиперплоскости. | ||
| + | Аналогично происходит и в случае нескольких характеристик: | ||
| + | |||
| + | <tex>f_{S}(g(z)) = \Lambda N^{T}z</tex>, где <tex>\Lambda</tex> {{---}} диагональная матрица с линейными коэффициентами <tex>\lambda_{i}</tex> для каждой из характеристик, <tex>N = [n_1, . . . , n_m]</tex> $-$ вектора нормалей для гиперплоскостей, разделяющих значения признаков <tex>1..m</tex>. | ||
| + | |||
| + | В случае если <tex>\Lambda</tex> {{---}} диагональная, то проблемы запутывания нет. | ||
| + | |||
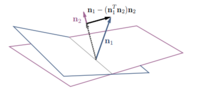
| + | В противном случае проделаем манипуляции в скрытом подпространстве (рис. 7). Проецируя <tex>n_1</tex> на <tex>n_2</tex> и вычитая полученный вектор из <tex>n_1</tex>, получаем такое направление <tex>n_1 - (n_1^{T} - n_2)n_2</tex> в скрытом пространстве, что вдоль этих направлений у сгенерированных изображений будет изменяться характеристика $1$ вне зависимости от характеристики $2$. | ||
| + | |||
| + | При слишком большом "расстоянии" от гиперплоскости соответствующая характеристика слишком сильно делает лицо непохожим на изначальное, но это объяснимо нормальным распределением вектора шума. | ||
| + | |||
| + | Также в скрытом пространстве имеют место арифмитические операции. То есть можно складывать и вычитать вектора из этого пространства, чтобы как получать промежуточные результаты, так и убирать или добавлять какую-либо характеристику. | ||
| + | |||
| + | Для борьбы с проблемой запутывания существуют и другие подходы: один из них представляет из себя разложение изображения на передний и задний слои (с возможными промежуточными слоями)<ref>[https://openaccess.thecvf.com/content_CVPR_2020/papers/Alharbi_Disentangled_Image_Generation_Through_Structured_Noise_Injection_CVPR_2020_paper.pdf Yazeed Alharbi, Peter Wonka {{---}} Disentangled Image Generation Through Structured Noise Injection, 3.3]</ref>. | ||
| + | |||
| + | Следующий метод основан на том факте, что существуют как локальные черты, так и глобальные. К первым можно отнести форму отдельной части лица, а ко вторым $-$ возраст и пол. Иногда изменение локальной черты может очень сильно влиять на глобальную. Этого хочется избежать, для этого некоторые размерности вектора шума применяются к каждой остальной размерности<ref>[https://openaccess.thecvf.com/content_CVPR_2020/papers/Alharbi_Disentangled_Image_Generation_Through_Structured_Noise_Injection_CVPR_2020_paper.pdf Yazeed Alharbi, Peter Wonka {{---}} Disentangled Image Generation Through Structured Noise Injection, 3.5]</ref>. | ||
==Применение== | ==Применение== | ||
| − | [[File:прогресс_ганов.jpg|450px|thumb|right|Прогресс в генерации фотографий с помощью GAN. Источник: https://twitter.com/goodfellow_ian]] | + | [[File:прогресс_ганов.jpg|450px|thumb|right|Рисунок 8. Прогресс в генерации фотографий с помощью GAN. Источник: https://twitter.com/goodfellow_ian]] |
| − | Чаще всего GAN'ы используются для генерации реалистичных фотографий. Серьезные улучшения в этом направлении были сделаны следующими работами: | + | Чаще всего GAN'ы используются для генерации реалистичных фотографий (рис. 8). Серьезные улучшения в этом направлении были сделаны следующими работами: |
* Auxiliary GAN<ref> [https://arxiv.org/pdf/1610.09585.pdf Augustus Odena {{---}} Conditional Image Synthesis with Auxiliary Classifier GANs]</ref>: вариант GAN-архитектуры, использующий метки данных; | * Auxiliary GAN<ref> [https://arxiv.org/pdf/1610.09585.pdf Augustus Odena {{---}} Conditional Image Synthesis with Auxiliary Classifier GANs]</ref>: вариант GAN-архитектуры, использующий метки данных; | ||
| Строка 73: | Строка 147: | ||
==CGAN (Conditional Generative Adversarial Nets)== | ==CGAN (Conditional Generative Adversarial Nets)== | ||
| − | [[File:CGAN_architecture.png|450px|thumb| | + | [[File:CGAN_architecture.png|450px|thumb|Рисунок 9. Архитектура CGAN. Источник: https://arxiv.org/pdf/1411.1784.pdf]] |
| − | '''Условные порождающие состязательные сети''' (англ. ''Conditional Generative Adversarial Nets, CGAN'') $-$ это модифицированная версия алгоритма GAN, которая может быть сконструирована при помощи передачи дополнительных данных '''y''', являющихся условием для генератора и дискриминатора. '''y''' может быть любой дополнительной информацией, например, меткой класса, изображением или данными из других моделей, что может позволить контролировать процесс генерации данных. Например, можно подавать параметр '''y''', как условие на класс для генерации чисел, похожих на MNIST. Создание таких картинок, в случае передачи картинки в качетсве '''y''' является [[:Задача трансляции изображений|задачей трансляции изображений]]. Пример работы ''CGAN'' на датасете ''MNIST'' с метками классов представленных в виде [[:Векторное представление слов|''one-hot'']] векторов <ref>[https://arxiv.org/pdf/1411.1784.pdf CGAN]</ref> | + | '''Условные порождающие состязательные сети''' (англ. ''Conditional Generative Adversarial Nets, CGAN'') $-$ это модифицированная версия алгоритма GAN, которая может быть сконструирована при помощи передачи дополнительных данных '''y''', являющихся условием для генератора и дискриминатора. '''y''' может быть любой дополнительной информацией, например, меткой класса, изображением или данными из других моделей, что может позволить контролировать процесс генерации данных. Например, можно подавать параметр '''y''', как условие на класс для генерации чисел, похожих на MNIST. Создание таких картинок, в случае передачи картинки в качетсве '''y''' является [[:Задача трансляции изображений|задачей трансляции изображений]]. Пример работы ''CGAN'' на датасете ''MNIST'' с метками классов представленных в виде [[:Векторное представление слов|''one-hot'']] векторов <ref>[https://arxiv.org/pdf/1411.1784.pdf CGAN]</ref> (рис. 9). |
| − | [[File:CGAN_generated.png|450px|thumb|center|Цифры, сгенерированные с помощью CGAN. Источник: https://arxiv.org/pdf/1411.1784.pdf]] | + | [[File:CGAN_generated.png|450px|thumb|center|Рисунок 10. Цифры, сгенерированные с помощью CGAN. Источник: https://arxiv.org/pdf/1411.1784.pdf]] |
| − | [[File:CGAN_generated_tags.PNG|450px|thumb|right| | + | [[File:CGAN_generated_tags.PNG|450px|thumb|right|Рисунок 11. Описание картинки. Источник: https://arxiv.org/pdf/1411.1784.pdf]] |
| − | Как уже было упомянуто на вход генератора и дискримантора из GAN подается дополнительная информация '''y''', например в случае с многослойными перецептронами условие может быть представлено дополнительным входным слоем. ( | + | Как уже было упомянуто на вход генератора и дискримантора из GAN подается дополнительная информация '''y''', например в случае с многослойными перецептронами условие может быть представлено дополнительным входным слоем. (рис. 9) |
В генераторе априорная вероятность шума <tex>p_{z}(z)</tex> и условие <tex>y</tex> комбинируются в объединённое скрытое представление, а состязательная тренирующая модель (Обе сети пытаются оптимизировать целевую функцию или функцию потерь. Когда дискриминатор меняет свое поведение, то и генератор меняет, и наоборот) предоставляет достаточно свободы в том как это представление составляется.<ref>[https://arxiv.org/pdf/1207.4404.pdf Yoshua Bengio, Gre ́goire Mesnil, Yann Dauphin and Salah Rifai {{---}} Better Mixing via Deep Representations ]</ref> | В генераторе априорная вероятность шума <tex>p_{z}(z)</tex> и условие <tex>y</tex> комбинируются в объединённое скрытое представление, а состязательная тренирующая модель (Обе сети пытаются оптимизировать целевую функцию или функцию потерь. Когда дискриминатор меняет свое поведение, то и генератор меняет, и наоборот) предоставляет достаточно свободы в том как это представление составляется.<ref>[https://arxiv.org/pdf/1207.4404.pdf Yoshua Bengio, Gre ́goire Mesnil, Yann Dauphin and Salah Rifai {{---}} Better Mixing via Deep Representations ]</ref> | ||
В дискриминаторе '''x''' и '''y''' представлены как входные параметры. | В дискриминаторе '''x''' и '''y''' представлены как входные параметры. | ||
| Строка 91: | Строка 165: | ||
В качестве примера использования данного алгоритма можно рассмотреть задачу генерации рукописных цифр. | В качестве примера использования данного алгоритма можно рассмотреть задачу генерации рукописных цифр. | ||
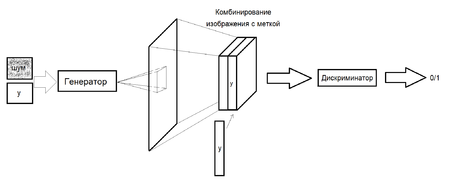
| − | При создании изображения в генератор поступает скомбинированная информация двух параметров: '''y''' и | + | При создании изображения в генератор поступает скомбинированная информация двух параметров: '''y''' и вектора шума. В случае ''MNIST'' это может быть, например, просто метка класса (от 0 до 9). На выходе из генератора поступает изображение, полученное с помощью транспонированной свертки (происходит деконволюция). Затем полученное изображение комбинируется с '''y''' и поступает в дискриминатор, который в свою очередь применяет свертку, чтобы получить полносвязный слой. Наконец, анализируя полученную информацию (полносвязный слой) дискриминатор принимает решение, является ли изображение сгенерированным. (рис. 12) |
| − | [[File:CGAN_gen_disc_v2.png|450px|thumb|center|Генерация при использовании CGAN]] | + | [[File:CGAN_gen_disc_v2.png|450px|thumb|center|Рисунок 12. Генерация при использовании CGAN]] |
| − | |||
| − | |||
| + | Также, используя условные порождающие состязательные сети, можно научить такую сеть генерировать текст по картинке и наоборот. В качестве параметра '''y''' в данном случае передается изображение, которое будет описано (рис. 11). | ||
| − | Более того, для такого типа нейронных сетей, принимающих в качестве параметра '''у''' некоротое изображение местности, в результате может быть получено аналогичное изображение этого места зимой или летом, днем или ночью. Такая задача является [[:Задача трансляции изображений|задачей трансляции изображений]] | + | Более того, для такого типа нейронных сетей, принимающих в качестве параметра '''у''' некоротое изображение местности, в результате может быть получено аналогичное изображение этого места зимой или летом, днем или ночью. Такая задача является [[:Задача трансляции изображений|задачей трансляции изображений]]. |
==DCGAN (Deep Convolutional Generative Adversarial Nets)== | ==DCGAN (Deep Convolutional Generative Adversarial Nets)== | ||
| − | [[File:DCGAN_generator.png|450px|thumb|right|Архитектура генератора в DCGAN. Источник: https://arxiv.org/pdf/1511.06434.pdf]] | + | [[File:DCGAN_generator.png|450px|thumb|right|Рисунок 13. Архитектура генератора в DCGAN. Источник: https://arxiv.org/pdf/1511.06434.pdf]] |
| − | '''DCGAN''' $-$ модификация алгоритма ''GAN'', в основе которых лежат сверточные нейронные сети (''CNN''). Задача поиска удобного представления признаков на больших объемах не размеченных данных является одной из наибольнее активных сфер исследований, в частности представление изображений и видио. Одним из удобных способов поиска представлений может быть '''DCGAN'''. Использование сверточных нейронных сетей напрямую не давало хороших результатов, поэтому было внесены ограничения на слои сверток. Эти ограничения и лежат в основе '''DCGAN''': | + | '''DCGAN''' $-$ модификация алгоритма ''GAN'', в основе которых лежат сверточные нейронные сети (''CNN''). Задача поиска удобного представления признаков на больших объемах не размеченных данных является одной из наибольнее активных сфер исследований, в частности представление изображений и видио. Одним из удобных способов поиска представлений может быть '''DCGAN''' (рис. 13). Использование сверточных нейронных сетей напрямую не давало хороших результатов, поэтому было внесены ограничения на слои сверток. Эти ограничения и лежат в основе '''DCGAN''': |
* Замена всех пулинговых слоев на страйдинговые свертки (''strided convolutions'') в дискриминаторе и частично-страйдинговые свертки (''fractional-strided-convolutions'') в генераторе, что позволяет сетям находить подходящие понижения и повышения размерностей; | * Замена всех пулинговых слоев на страйдинговые свертки (''strided convolutions'') в дискриминаторе и частично-страйдинговые свертки (''fractional-strided-convolutions'') в генераторе, что позволяет сетям находить подходящие понижения и повышения размерностей; | ||
| Строка 115: | Строка 188: | ||
<tex> 4 \times 4 </tex> и получить общий вектор признаков на их основе. ''L2-SVM'', c полученным представлением, на наборе данных ''CIFAR-10''<ref name="datasets" /> превосходит по точности решения, основанные на алгоритме | <tex> 4 \times 4 </tex> и получить общий вектор признаков на их основе. ''L2-SVM'', c полученным представлением, на наборе данных ''CIFAR-10''<ref name="datasets" /> превосходит по точности решения, основанные на алгоритме | ||
''K-Means''. Подробнее об этом вы можете прочитать в статье. <ref> [https://arxiv.org/pdf/1511.06434.pdf Alec Radford, Luke Metz, Soumith Chintala {{---}} Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks]</ref> | ''K-Means''. Подробнее об этом вы можете прочитать в статье. <ref> [https://arxiv.org/pdf/1511.06434.pdf Alec Radford, Luke Metz, Soumith Chintala {{---}} Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks]</ref> | ||
| − | |||
==StackGAN (Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks)== | ==StackGAN (Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks)== | ||
| − | [[File:StackGANexample.jpg|400px|thumb|right| Пример работы порождающей состязателной сети для генерации фото-реалистичных изображений StackGAN. Источник: https://arxiv.org/pdf/1612.03242.pdf]] | + | [[File:StackGANexample.jpg|400px|thumb|right|Рисунок 14. Пример работы порождающей состязателной сети для генерации фото-реалистичных изображений StackGAN. Источник: https://arxiv.org/pdf/1612.03242.pdf]] |
'''StackGAN''' $-$ порождающая состязательная сеть для генерации фото-реалистичных изображений (256x256) исходя из текстового описания. Генерировать фото-реалистичные изображения на обычных GAN сложно, поэтому была придумана двух-этапная модель генерации. Stage-I GAN рисует скетчи с примитивными формами и цветами, основанные на текстовом описании, в низком разрешении. Stage-II GAN принимает на вход изображения с первого этапа и текстовое описание и генерирует изображение в высоком разрешении с фото-реалистичными деталями. Чтобы улучшить разнообразие синтезированных изображений и стабилизировать обучение, вместо CGAN использовался метод Conditioning Augmentation. | '''StackGAN''' $-$ порождающая состязательная сеть для генерации фото-реалистичных изображений (256x256) исходя из текстового описания. Генерировать фото-реалистичные изображения на обычных GAN сложно, поэтому была придумана двух-этапная модель генерации. Stage-I GAN рисует скетчи с примитивными формами и цветами, основанные на текстовом описании, в низком разрешении. Stage-II GAN принимает на вход изображения с первого этапа и текстовое описание и генерирует изображение в высоком разрешении с фото-реалистичными деталями. Чтобы улучшить разнообразие синтезированных изображений и стабилизировать обучение, вместо CGAN использовался метод Conditioning Augmentation. | ||
| Строка 125: | Строка 197: | ||
Раннее использовались CGAN, поскольку на вход им можно было подавать условия, но просто добавляя слои, увеличивающие размер изображения, достичь хороших результатов не удалось. Поэтому основной задачей было повысить разрешение изображений. | Раннее использовались CGAN, поскольку на вход им можно было подавать условия, но просто добавляя слои, увеличивающие размер изображения, достичь хороших результатов не удалось. Поэтому основной задачей было повысить разрешение изображений. | ||
| − | Одной из ключевых особенностей StackGAN является Conditioning Augmentation, так как оно позволило расширить количество примеров тренировочного сета, путем небольших случайных изменений в исходных изображениях, что увеличивало многообразие данных. Как показано на картинке, текстовое описание <tex>t</tex> кодировщиком переводится в векторное представление <tex>\varphi_{t}</tex>. Раннее векторное представление нелинейно трансформировалось, чтобы получить скрытые условные переменные, которые подавались на вход генератору, однако простарнство значений скрытых переменных имеет большую размерность, что приводило к разрывам в многообразии данных, что не выгодно для генератора. Чтобы избавиться от этого как раз нужно Conditioning Augmentation, которое в отличии от предоставления фиксированных значений переменных выбирает их из нормального распределения <tex>\mathcal{N}(\mu(\varphi_{t}), \Sigma(\varphi_{t}))</tex>, где среднее значение <tex>\mu(\varphi_{t})</tex> и ковариация <tex>\Sigma(\varphi_{t}))</tex> это функции от входного вектора <tex>\varphi_{t}</tex>. В добавок к уже упомянотому, чтобы сделать многообразие гладким и не переобучиться, нужно добавить регуляризацию, <tex>D_{KL}(\mathcal{N}(\mu(\varphi_{t}), \Sigma(\varphi_{t})) || \mathcal{N}(0, I))</tex> (KL divergence)<ref> [https://ru.wikipedia.org/wiki/Расстояние_Кульбака_—_Лейблера Kullback-Leibler divergence]</ref>. | + | Одной из ключевых особенностей StackGAN является Conditioning Augmentation, так как оно позволило расширить количество примеров тренировочного сета, путем небольших случайных изменений в исходных изображениях, что увеличивало многообразие данных. Как показано на картинке, текстовое описание <tex>t</tex> кодировщиком переводится в векторное представление <tex>\varphi_{t}</tex> (рис. 15). Раннее векторное представление нелинейно трансформировалось, чтобы получить скрытые условные переменные, которые подавались на вход генератору, однако простарнство значений скрытых переменных имеет большую размерность, что приводило к разрывам в многообразии данных, что не выгодно для генератора. Чтобы избавиться от этого как раз нужно Conditioning Augmentation, которое в отличии от предоставления фиксированных значений переменных выбирает их из нормального распределения <tex>\mathcal{N}(\mu(\varphi_{t}), \Sigma(\varphi_{t}))</tex>, где среднее значение <tex>\mu(\varphi_{t})</tex> и ковариация <tex>\Sigma(\varphi_{t}))</tex> это функции от входного вектора <tex>\varphi_{t}</tex>. В добавок к уже упомянотому, чтобы сделать многообразие гладким и не переобучиться, нужно добавить регуляризацию, <tex>D_{KL}(\mathcal{N}(\mu(\varphi_{t}), \Sigma(\varphi_{t})) || \mathcal{N}(0, I))</tex> (KL divergence)<ref> [https://ru.wikipedia.org/wiki/Расстояние_Кульбака_—_Лейблера Kullback-Leibler divergence]</ref>. |
| − | [[File:StackGANProcess.jpg| | + | [[File:StackGANProcess.jpg|1000px|thumb|center|Рисунок 15. Процесс обучения StackGAN. Источник: https://arxiv.org/pdf/1612.03242.pdf]] |
Stage-I GAN тренирует дискриминатор <tex>D_{0}</tex> и генератор <tex>G_{0}</tex> поочередной максимизицаии <tex>L_{D_{0}}</tex> и минимизации <tex>L_{G_{0}}</tex>, как указано в уравенинях: | Stage-I GAN тренирует дискриминатор <tex>D_{0}</tex> и генератор <tex>G_{0}</tex> поочередной максимизицаии <tex>L_{D_{0}}</tex> и минимизации <tex>L_{G_{0}}</tex>, как указано в уравенинях: | ||
<center><tex>L_{D_0} = E_{(I_0, t)\sim p_{data}}[\log D_{0}(I_0, \varphi_t)] + E_{z\sim t, t \sim p_{data}}[\log (1 - D_0(G_{0}(z, \hat{c_0}), \varphi_t))]</tex></center> | <center><tex>L_{D_0} = E_{(I_0, t)\sim p_{data}}[\log D_{0}(I_0, \varphi_t)] + E_{z\sim t, t \sim p_{data}}[\log (1 - D_0(G_{0}(z, \hat{c_0}), \varphi_t))]</tex></center> | ||
| Строка 135: | Строка 207: | ||
<center><tex>L_{D} = E_{(I, t)\sim p_{data}}[\log D(I, \varphi_t)] + E_{s_0\sim p_{G_0}, t \sim p_{data}}[\log (1 - D(G(s_0, \hat{c}), \varphi_t))]</tex></center> | <center><tex>L_{D} = E_{(I, t)\sim p_{data}}[\log D(I, \varphi_t)] + E_{s_0\sim p_{G_0}, t \sim p_{data}}[\log (1 - D(G(s_0, \hat{c}), \varphi_t))]</tex></center> | ||
<center><tex>L_{G} = E_{s_0\sim p_{G_0}, t \sim p_{data}}[\log (1 - D(G(s_0, \hat{c}), \varphi_t))] + \lambda D_{KL}(\mathcal{N}(\mu(\varphi_{t}), \Sigma(\varphi_{t}) || \mathcal{N}(0, I))</tex></center> | <center><tex>L_{G} = E_{s_0\sim p_{G_0}, t \sim p_{data}}[\log (1 - D(G(s_0, \hat{c}), \varphi_t))] + \lambda D_{KL}(\mathcal{N}(\mu(\varphi_{t}), \Sigma(\varphi_{t}) || \mathcal{N}(0, I))</tex></center> | ||
| − | Где <tex>s_0 = G_0(z,\hat{c_0})</tex> результат работы генератора Stage-I GAN и скрытый параметр <tex>\hat{c}</tex> подаются на вход дискриминатору и генератору Stage-II GAN, при этом на вход не подается случайное значение, как на первой стадии, поскольку хватает подачи случайного <tex>z</tex> на вход Stage-I GAN. При этом Stage-I GAN и Stage-II GAN имеют разные полно-связные слои, чтобы отличаться по среднему значению и стандартному отклонению, таким образом на разных этапах фокусируюемся на разных деталях исходного текста. | + | Где <tex>s_0 = G_0(z,\hat{c_0})</tex> результат работы генератора Stage-I GAN и скрытый параметр <tex>\hat{c}</tex> подаются на вход дискриминатору и генератору Stage-II GAN, при этом на вход не подается случайное значение, как на первой стадии, поскольку хватает подачи случайного <tex>z</tex> на вход Stage-I GAN. При этом Stage-I GAN и Stage-II GAN имеют разные полно-связные слои, чтобы отличаться по среднему значению и стандартному отклонению, таким образом на разных этапах фокусируюемся на разных деталях исходного текста (рис. 14). |
==LAPGAN (Laplacian Pyramid of Adversarial Networks)== | ==LAPGAN (Laplacian Pyramid of Adversarial Networks)== | ||
| − | |||
'''LAPGAN''' $-$ генеративная параметрическая модель, представленная пирамидой лапласианов с каскадом сверточных нейронных сетей внутри, которая генерирует изображения постепенно от исходного изображения с низким разрешением к изображению с высоким. На каждом уровне пирамиды обучается сверточная генеративная модель, используя подход порождающих состязательных сетей. Такая стратегия позволяет декомпозировать задачу генерации изображений на последовательность уровней, что упрощает ее решение. | '''LAPGAN''' $-$ генеративная параметрическая модель, представленная пирамидой лапласианов с каскадом сверточных нейронных сетей внутри, которая генерирует изображения постепенно от исходного изображения с низким разрешением к изображению с высоким. На каждом уровне пирамиды обучается сверточная генеративная модель, используя подход порождающих состязательных сетей. Такая стратегия позволяет декомпозировать задачу генерации изображений на последовательность уровней, что упрощает ее решение. | ||
| + | |||
| + | [[File:LAPGANtest.jpg|500px|thumb|right|Рисунок 16. Процедура семплинга для модели LAPGAN. Источник: https://arxiv.org/pdf/1506.05751.pdf]] | ||
Пирамида лапласианов $-$ это линейное обратимое представление изображений, состоящее из набора частотных полос изображений. Пусть <tex>d(\cdot)</tex> - это операция сжатия изображения размера <tex>j \times j</tex> так, что новое изображение <tex>d(I)</tex> имеет размеры <tex>j/2 \times j/2</tex>, также <tex>u(\cdot)</tex> - операция расширения такой, что <tex>u(I)</tex> имеет размеры <tex>2j \times 2j</tex>. Тогда пирамида гаусианов имеет вид <tex>\mathcal{G}(I) = [I_0, I_1,..., I_k]</tex>, где <tex>I_0 = I</tex> и <tex>I_k</tex> представляет собой <tex>k</tex> раз выполненное применение <tex>d(\cdot)</tex>. Коэффициенты <tex>h_k</tex> на каждом уровне пирамиды лапласианов считаются так: | Пирамида лапласианов $-$ это линейное обратимое представление изображений, состоящее из набора частотных полос изображений. Пусть <tex>d(\cdot)</tex> - это операция сжатия изображения размера <tex>j \times j</tex> так, что новое изображение <tex>d(I)</tex> имеет размеры <tex>j/2 \times j/2</tex>, также <tex>u(\cdot)</tex> - операция расширения такой, что <tex>u(I)</tex> имеет размеры <tex>2j \times 2j</tex>. Тогда пирамида гаусианов имеет вид <tex>\mathcal{G}(I) = [I_0, I_1,..., I_k]</tex>, где <tex>I_0 = I</tex> и <tex>I_k</tex> представляет собой <tex>k</tex> раз выполненное применение <tex>d(\cdot)</tex>. Коэффициенты <tex>h_k</tex> на каждом уровне пирамиды лапласианов считаются так: | ||
| Строка 148: | Строка 221: | ||
<center><tex>I_k = u(I_{k + 1}) + h_k</tex></center> | <center><tex>I_k = u(I_{k + 1}) + h_k</tex></center> | ||
| − | [[File:LAPGANtrain.jpg|500px|thumb|right|Процедура обучения модели LAPGAN. Источник: https://arxiv.org/pdf/1506.05751.pdf]] | + | [[File:LAPGANtrain.jpg|500px|thumb|right|Рисунок 17. Процедура обучения модели LAPGAN. Источник: https://arxiv.org/pdf/1506.05751.pdf]] |
| − | |||
Подход представленный в '''LAPGAN''' работает по такому же принципу, только на каждому шаге вместо коэфициентов <tex>h_k</tex> используются генераторы <tex>\{G_0,G_1,...,G_k\}</tex>, каждый из которых захватывает распределение коэфициентов <tex>h_k</tex> для реальных изображений на разных уровнях пирамиды лапласиана: | Подход представленный в '''LAPGAN''' работает по такому же принципу, только на каждому шаге вместо коэфициентов <tex>h_k</tex> используются генераторы <tex>\{G_0,G_1,...,G_k\}</tex>, каждый из которых захватывает распределение коэфициентов <tex>h_k</tex> для реальных изображений на разных уровнях пирамиды лапласиана: | ||
<center><tex>\tilde{I_k} = u(\tilde{I_{k + 1}}) + \tilde{h_k} = u(\tilde{I_{k + 1}}) + G_k(z_k, u(\tilde{I_{k + 1}}))</tex></center> | <center><tex>\tilde{I_k} = u(\tilde{I_{k + 1}}) + \tilde{h_k} = u(\tilde{I_{k + 1}}) + G_k(z_k, u(\tilde{I_{k + 1}}))</tex></center> | ||
| − | Процедура семплинга для нашей модели '''LAPGAN'''. Начинаем с шума <tex>z_3</tex> и используем генеративную модель <tex>G_3</tex> для создания <tex>\tilde{I_3}</tex>. Потом расширяем изображение до <tex>l_2</tex> для следующиего уровня генерации <tex>G_2</tex>. Вместе с еще одним шумом <tex>z_2</tex> получаем изображение различия <tex>\tilde{I_2}</tex>. Продолжаем процесс, пока не получим <tex>I_0</tex>. | + | Процедура семплинга для нашей модели '''LAPGAN''' (рис. 16). Начинаем с шума <tex>z_3</tex> и используем генеративную модель <tex>G_3</tex> для создания <tex>\tilde{I_3}</tex>. Потом расширяем изображение до <tex>l_2</tex> для следующиего уровня генерации <tex>G_2</tex>. Вместе с еще одним шумом <tex>z_2</tex> получаем изображение различия <tex>\tilde{I_2}</tex>. Продолжаем процесс, пока не получим <tex>I_0</tex>. |
| + | |||
| + | |||
| + | Процедура обучения '''LAPGAN''' (рис. 17). Начинаем с изображения <tex>I</tex> размера <tex>64 \times 64</tex> из тренировчного набора. Берем <tex>I_0 = I </tex> и сжимаем его(красная стрелка) чтобы получить <tex>I_1</tex>; затем расширяем его(зеленая стрелка), чтобы получить <tex>l_0</tex> низко-частотное изображение <tex>I_0</tex>; с равной вероятностью используем его для создния либо реального, либо сгенерированного примера для дискриминатора <tex>D_0</tex>. В случае реального изображения(синяя стрелка) считаем цветовой контраст <tex>h_0 = I_0 - l_0</tex>, которая подается на вход дискриминатору <tex>D_0</tex>, для опредления реальное изображение или нет. В случае сгенерированного(розовая стрелка), генеративная сеть <tex>G_0</tex> получает на вход шум <tex>z_0</tex> и <tex>l_0</tex>. Оно генерирует цветовой контраст <tex>\tilde{h_0} = G_0(z_0,l_0)</tex>, который подается на вход <tex>D_0</tex>. В обоих случаях дискриминатор также получает <tex>l_0</tex> (оранжевая стрелка). Оптимизируя минмакс игру условной порождающей сети <tex>G_0</tex> учится генерировать реалистичную высоко-частотную структуру <tex>\tilde{h_0}</tex> с помощью низко-частотного представления <tex>l_0</tex>. Такая процедура проходит на всех слоях, кроме последнего, где можно уже использовать обычный GAN. | ||
| + | |||
| + | ==ControlGAN (Controllable Generative Adversarial Networks)== | ||
| + | |||
| + | [[File:ControlGANConcept.png|350px|thumb|right|Рисунок 18. Концепт модели ControlGAN. Источник: <tex>\href{https://arxiv.org/pdf/1708.00598.pdf}{\text{[x]}}</tex>]] | ||
| + | |||
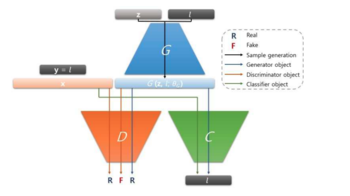
| + | Контролируемые порождающие состязательные сети (англ. Controllable Generative Adversarial Nets, '''ControlGAN''') $-$ модифицированная версия алгоритма GAN, состоящая из трех нейронных сетей: генератор, дискриминатор, классификатор. Концепт модели ControlGAN (рис. 18). Как и в обычной версии алгоритма, генератор пытается обмануть дискриминатор, и одновременно с этим пытается быть классифицированным как нужный класс в классификаторе. | ||
| + | |||
| + | Хоть CGAN и являются самыми популярными моделями для генерации образцов, зависимых от внешних данных, но лучше они умеют генерировать образцы с заданными ярко отличительными чертами (цвет волос, веснушки), но менее явные детали (форма бровей, сережки) вызывают затруднения (Но более поздний StyleGAN2 справляется и с этой задачей). C помощью отделения классификатора от дискриминатора, ControlGAN позволяет контролировать черты образцов. К тому же и само качество сгенерированных изображений может быть улучшено засчет того, что такое разделение на три составляющие дает возможность дискриминатору лучше выполнять свою главную задачу. | ||
| + | |||
| + | Более того, аугментация данных может помешать некоторым сетям, например, Auxiliary Classifier GAN (ACGAN) обучаться, хотя сам способ может улучшить качество классификации. К тому же в случае контролируемой генерации нет необходимости размечать тренировочные данные, выбираются желаемые характеристики объектов для генерации, а не условная информация (например, метка объекта). | ||
| + | |||
| + | [[File:ControlGANPrinciple.png|200px|thumb|right|Рисунок 19. | ||
| + | Принцип работы. Источник:<tex>\href{https://arxiv.org/pdf/1708.00598.pdf}{\text{[x]}}</tex>]] | ||
| + | |||
| + | Иллюстрация принципа работы сети (рис. 19). Зеленые линии $-$ результат работы классификатора; оранжевые $-$ дискриминатора. Серые фигуры $-$ образцы из разных классов. Результат генератора обозначается голубыми участками, которыми он показывает распределение образцов, как и пытается быть классифицированным верно. | ||
| + | |||
| + | ControlGAN минимизирует следующие уравнения: | ||
| + | |||
| + | <tex>\delta_D = arg min\{\alpha L_D(t_D, D(x;\delta_D)) + (1 - \alpha)L_D((1 - t_D), D(G(z, l; \delta_G);\delta_D))\}</tex>, | ||
| + | |||
| + | <tex>\delta_D = arg min\{\gamma_t L_C(l, G(z, l; \delta_G)) + L_D(t_D, D(G(z, l; \delta_G);\delta_D)\}</tex>, | ||
| + | |||
| + | <tex>\delta_C = arg min\{L_C(l, x; \delta_C)\}</tex>. | ||
| + | |||
| + | <tex>t_D</tex> $-$ метка для генератора, <tex>\alpha</tex> $-$ параметр для дискриминатора, <tex>\gamma_t</tex> $-$ параметр для входных меток на генератор, <tex>l</tex> $-$ метки образца <tex>x</tex>. | ||
| + | |||
| + | <tex>E</tex> $-$ отношение между ошибками классификации сгенерированных образцов и изначальных данных. Для тренировки генератора используем оценочное значение <tex>\hat{E}</tex>, полученное, использующее классификатор и генератор из сети. При значении <tex>\hat{E}</tex> меньше $1$, генератор обучается на входных данных, иначе обучается генерировать образцы. С помощью этого параметра ControlGAN управляет, чему из вышеперечисленного обучаться. Сам параметр поддерживает постоянной отношение между ошибками. | ||
| + | |||
| + | <tex>E = \dfrac{L_C(l,G(z,l;\delta_G))}{L_C(l, x)}</tex>, | ||
| + | <tex>\gamma_t = \gamma_{t - 1} + r \{L_C(l, G(z,l;\delta_G)) - \hat{E} \cdot L_C(l, x)\}</tex>, | ||
| − | + | <tex>r</tex> $-$ коэффициент обучения для <tex>\gamma_t</tex>. | |
==См. также== | ==См. также== | ||
| Строка 172: | Строка 277: | ||
* [https://arxiv.org/pdf/1612.03242.pdf StackGAN Paper] | * [https://arxiv.org/pdf/1612.03242.pdf StackGAN Paper] | ||
* [https://arxiv.org/pdf/1506.05751.pdf LAPGAN Paper] | * [https://arxiv.org/pdf/1506.05751.pdf LAPGAN Paper] | ||
| + | * [https://arxiv.org/pdf/1708.00598.pdf ControlGAN Paper] | ||
| + | * [https://arxiv.org/pdf/1907.10786.pdf Interpreting the Latent Space Paper] | ||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Порождающие модели]] | [[Категория: Порождающие модели]] | ||
Текущая версия на 19:29, 4 сентября 2022
Порождающие состязательные сети (англ. Generative Adversarial Nets, GAN) — алгоритм машинного обучения, входящий в семейство порождающих моделей и построенный на комбинации из двух нейронных сетей: генеративная модель , которая строит приближение распределения данных, и дискриминативная модель , оценивающая вероятность, что образец пришел из тренировочных данных, а не сгенерированных моделью (рис. 1). Обучение для модели заключается в максимизации вероятности ошибки дискрминатора . Впервые такие сети были представлены Иэном Гудфеллоу в 2014 году.
Содержание
- 1 Постановка задачи и метод
- 2 Интуитивный процесс тренировки
- 3 Оригинальный алгоритм обучения GAN
- 4 Проблемы обучения GAN
- 5 Применение
- 6 CGAN (Conditional Generative Adversarial Nets)
- 7 DCGAN (Deep Convolutional Generative Adversarial Nets)
- 8 StackGAN (Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks)
- 9 LAPGAN (Laplacian Pyramid of Adversarial Networks)
- 10 ControlGAN (Controllable Generative Adversarial Networks)
- 11 См. также
- 12 Примечания
- 13 Источники информации
Постановка задачи и метод
Как было указано ранее в описании метода, мы хотим обучить две модели: генеративную и дискриминативную. Поскольку, удобнее всего использовать многослойные перцептроны для обучения состязательной модели, будем использовать именно их для детального описания работы модели. Чтобы вывести вероятностное распределение генератора над набором данных , определим априорную вероятность шума и представим генератор, как отображение , где дифференцируемая функция, представленная многослойным перцептроном с параметром . Аналогичным образом представим второй многослойный перцептрон , который на выход подает одно скалярное значение - вероятность того, что пришло из тренировочных данных, а не . Во время тренировки мы стремимся максимизировать вероятность правильной идентификации объектов из тренировочной и сгенерированной выборок. И в то же время тренируем так, чтобы минимизировать : Другими словами, и играют в "минимакс игру":
Интуитивный процесс тренировки
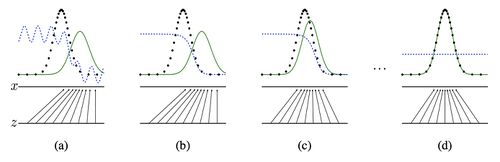
Как показано на рисунке 2, генеративные состязательные сети обучаются путем одновременного обновления дискриминирующего распределения ( синяя пунктирная линия), так чтобы дискриминатор мог различать объекты из распределения тренировочного сета(черная пунктирная в точку линия) и из распределения генератора ( зеленая сплошная линия). Нижняя горизонтальная линия представляет собой область, из которой составлена выборка , в нашем случае равномерно. Горизонтальная линия над ней является частью области . Стрелками на картинке показано, как отображение , накладывает неравномерное распределение на тренировочное. сжимается в областях с высокой плотностью и расширяется в областях с низкой. Рассмотрим описанный на картинках процесс. (a) Близкая сходимость состязающейся пары: похоже на распределение частично-точный классификатор. (b) Во внутреннем цикле алгоритма обучается отличать объекты из тренировочных данных, сходясь к . (c) После обновления градиент привел к передвижению в область, с большей вероятностью быть классифицированным как данные. (d) После нескольких шагов обучения и придут в состояние, в котором не смогу улучшиться, так как будет выполняться условие и дискриминатор не сможет различать два распределения и его выход всегда будет .
Оригинальный алгоритм обучения GAN
В процессе обучения требуется делать два шага оптимизации поочередно: сначала обновлять веса генератора при фиксированном , а затем веса дискриминатора при фиксированном . На практике дискриминатор обновляется раз вместо одного, поскольку, полностью оптимизировать дискриминатор вычислительно не выгодно и на конечных сетах он может переобучиться. Таким образом является гиперпараметром.
// num_iteration — число итераций обучения
function GAN:
for i = 1..num_iteration do
for j = 1..k do
//Получаем мини-батч $\{z_1, . . . , z_m\}$ из распределения $p_z$
$z$ = getBatchFromNoisePrior($p_z$)
//Получаем мини-батч $\{x_1, . . . , x_m\}$ из распределения $p_{data}$
$x$ = getBatchFromDataGeneratingDistribution($p_{data}$)
//Обновляем дискриминатор в сторону возрастания его градиента
end for
//Получаем мини-батч $\{z_1, . . . , z_m\}$ из распределения $p_z$
$z$ = getBatchFromNoisePrior($p_z$)
//Обновляем генератор в сторону убывания его градиента
end for
На практике не всегда удобно использовать уравнение описанной выше. В начале обучения, когда плохо настроен дискриминатор может не учитывать объекты, с высокой уверенностью в классификации, так как они сильно отличаются от тренировочного сета, в таком случае стагнирует. Чтобы избежать этого, можно вместо минимизации максимизировать . На рисунке 3 представлена зависимость получаемого изображения от итерации обучения.
Проблемы обучения GAN
Большинство GAN'ов подвержено следующим проблемам:
- Схлопывание мод распределения (англ. mode collapse): генератор коллапсирует, то есть выдает ограниченное количество разных образцов.
- Проблема стабильности обучения (англ. non-convergence): параметры модели дестабилизируются и не сходятся.
- Исчезающий градиент (англ. diminished gradient): дискриминатор становится слишком "сильным", а градиент генератора исчезает и обучение не происходит.
- Проблема запутывания (англ. disentanglement problem): выявление корреляции в признаках, не связанных (слабо связанных) в реальном мире.
- Высокая чувствительность к гиперпараметрам.
Часть этих проблем будет рассмотрена подробнее ниже, но нужно заметить, что универсального подхода к решению большинства из них нет. Зато существуют практические советы[1], которые могут помочь при обучении GAN'ов. Основными из них являются:
- Нормализация данных. Все признаки в диапазоне $[-1; 1]$;
- Замена функции ошибки для $G$ с $\min log (1-D)$ на $\max log D$, потому что исходный вариант имеет маленький градиент на раннем этапе обучения и большой градиент при сходимости, а предложенный наоборот;
- Сэмплирование из многомерного нормального распределения вместо равномерного;
- Использовать нормализационные слои (например, batch normalization или layer normalization) в $G$ и $D$;
- Использовать метки для данных, если они имеются, то есть обучать дискриминатор еще и классифицировать образцы.
Коллапс мод


В процессе обучения генератор может прийти к состоянию, при котором он будет всегда выдавать ограниченный набор выходов. При этом пространство, в котором распределены сгенерированные изображения, окажется существенно меньше, чем пространство исходных изображений. Главная причина этого в том, что генератор обучается обманывать дискриминатор, а не воспроизводить исходное распределение. Если генератор начинает каждый раз выдавать похожий выход, который является максимально правдоподобным для текущего дискриминатора, то зависимость от $z$ падает, а следовательно и градиент $G(z)$ стремиться к 0. Лучшей стратегией для дискриминатора будет улучшение детектирования этого конкретного изображения. Так на следующих итерациях наиболее вероятно, что генератор придет к другому изображению, хорошо обманывающему текущий дискриминатор, а дискриминатор будет учиться отличать конкретно это новое изображение. Этот процесс не будет сходиться и количество представленных мод не будет расти, поэтому приблизиться к исходному распределению не удастся. На рисунке 4 наглядно представлена проблема mode collapse и то как генератор "путешествует" по модам не приближаясь к целевому распределению. На рисунке 5 наглядно представлен пример mode collapse в процессе работы обычной GAN, обучаемой на датасете MNIST.
На текущий момент mode collape является одной из главных проблем GAN, эффективное решение которой ещё ищется. Возможные решения проблемы mode collapse:
- WGAN — использование метрики Вассерштейна (англ. Wasserstein Loss) внутри функции ошибки, позволяет дискриминатору быстрее обучаться выявлять повторяющиеся выходы, на которых стабилизируется генератор[2].
- UGAN (Unrolled GAN) — для генератора используется функция потерь, которая не только от того, как текущий дискриминатор оценивает выходы генератора, но и от выходов будущих версий дискриминатора.
Проблема стабильности обучения
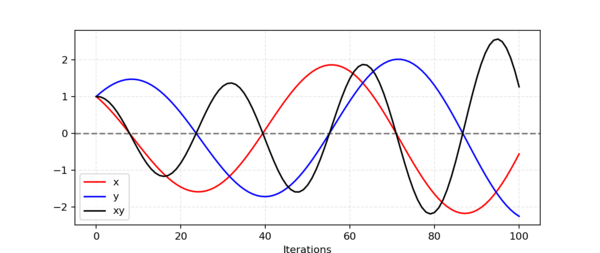
Задача обучения дискриминатора и генератора в общем смысле не является задачей поиска локального или глобального минимума функции, а является задачей поиска точки равновесия двух игроков. В теории игр эта точка называется точкой равновесия Нэша (англ. Nash equilibrium) в которой оба игрока больше не получают выгоды, хотя следуют оптимальной стратегии. Рассмотрим задачу поиска этой точки на игрушечном примере, где $G$ хочет максимизировать произведение $xy$ а $D$ — минимизировать. Будем обновлять параметры $x$ и $y$ на основе градиентного спуска: Если изобразить на графике поведение $x$,$y$ и $xy$ (рис. 6) то станет ясно, что они не сойдутся, а амплитуда их движения будет только увеличиваться.
В оригинальной статье про GAN используется дивергенция Дженсена-Шеннона (англ. Jensen–Shannon divergence), которая в свою очередь использует дивергенцию Кульбака-Лейблера (англ. Kullback-Leibler divergence):
- ,
где $P$ и $Q$ — $k$-мерные абсолютно непрерывные распределения, $p(x)$ и $q(x)$ — функции плотности этих распределений, заданные на . Нетрудно заметить, что при наличии $x$, в которых $q(x)=0$, весь интеграл разойдется, что плохо влияет на сходимость обучения.
Возможные решения проблемы стабильности:
- Регуляризация — Добавление шума ко входам дискриминатора и соответствующая настройка гиперпараметров дискриминатора.
- PGGAN (Progressive Growing of GANs, разработана NVidia[3]) — в процессе работы разрешение изображений увеличивается от очень малых (4 на 4 пикселя), до конечных (1024 на 1024 пикселя), что позволяет тренировать сначала выявление крупных черт а затем более мелких, что крайне положительно сказывается на стабильности.
- WGAN — В качестве функции дивергенции используется метрика Вассерштейна, которая в большинстве случаев решает проблему расходимости интеграла в функции Дженсена-Шеннона.
Проблема запутывания (Проблема связанности характеристик)
Сложность с генеративными состязательными сетями заключается в том, что непонятно, как им удается определять конкретные различные характеристики (возраст и пол, например) и связаны ли между собой эти характеристики.
Генератор хорошо обученной сети $-$ функция , где $-$ скрытое пространство размерности , для которого обычно применимо Гауссово распределение в многомерном случае. $-$ пространство изображений, где у каждого изображения существует набор характеристик вроде возраста или пола. Пусть нам дана функция оценки , где $-$ пространство изображений размерности . Тогда , где , $-$ связь между точкой в скрытом подпространстве и характеристиками получившегося изображения. Для функции оценок часто используют Inception score[4] и FID (Frechet Inception distance[5]), где главными критериями хорошо сгенерированных образцов является разнообразие отличительных черт в образцах и их выраженность.
Установлено, что при движении между двумя точками и характеристики меняются постепенно, без скачков. Тогда по этому направлению в $Z$ можно построить гиперплоскость. Тогда сделаем предположение, при котором для любого бинарного параметра существует гиперплоскость, что все образцы с одной стороны от нее имеют одинаковое значение этого параметра.
Заведем следующую функцию "расстояния": , где , $-$ вектор нормали гиперплоскости. Данная функция не подходит под определение расстояния из-за наличия отрицательных значений (но знак нам необходим для определения знака параметра характеристики). Ожидается, что есть близкая к линеной зависимость оценки $f$ по данному параметру от "расстояния":
.
В таком случае выраженность характеристики зависит от "расстояния" до этой гиперплоскости. Аналогично происходит и в случае нескольких характеристик:
, где — диагональная матрица с линейными коэффициентами для каждой из характеристик, $-$ вектора нормалей для гиперплоскостей, разделяющих значения признаков .
В случае если — диагональная, то проблемы запутывания нет.
В противном случае проделаем манипуляции в скрытом подпространстве (рис. 7). Проецируя на и вычитая полученный вектор из , получаем такое направление в скрытом пространстве, что вдоль этих направлений у сгенерированных изображений будет изменяться характеристика $1$ вне зависимости от характеристики $2$.
При слишком большом "расстоянии" от гиперплоскости соответствующая характеристика слишком сильно делает лицо непохожим на изначальное, но это объяснимо нормальным распределением вектора шума.
Также в скрытом пространстве имеют место арифмитические операции. То есть можно складывать и вычитать вектора из этого пространства, чтобы как получать промежуточные результаты, так и убирать или добавлять какую-либо характеристику.
Для борьбы с проблемой запутывания существуют и другие подходы: один из них представляет из себя разложение изображения на передний и задний слои (с возможными промежуточными слоями)[6].
Следующий метод основан на том факте, что существуют как локальные черты, так и глобальные. К первым можно отнести форму отдельной части лица, а ко вторым $-$ возраст и пол. Иногда изменение локальной черты может очень сильно влиять на глобальную. Этого хочется избежать, для этого некоторые размерности вектора шума применяются к каждой остальной размерности[7].
Применение

Чаще всего GAN'ы используются для генерации реалистичных фотографий (рис. 8). Серьезные улучшения в этом направлении были сделаны следующими работами:
- Auxiliary GAN[8]: вариант GAN-архитектуры, использующий метки данных;
- SN-GAN[9]: GAN с новым подходом решения проблемы нестабильного обучения через спектральную нормализацию;
- SAGAN[10]: GAN, основанный на механизме внимания;
- BigGAN[11]: GAN с ортогональной регуляризацией, позволившей разрешить проблему коллапсирования при долгом обучении;
Кроме простой генерации изображений, существуют достаточно необычные применения, дающие впечатляющие результаты не только на картинках, но и на звуке:
- CycleGAN[12]: меняет изображения c одного домена на другой, например, лошадей на зебр;
- SRGAN[13]: создает изображения с высоким разрешением из более низкого разрешения;
- Pix2Pix[14]: создает изображения по семантической окраске;
- StackGAN[15]: создает изображения по заданному тексту;
- MidiNet[16]: генерирует последовательность нот, таким образом, создает мелодию.
CGAN (Conditional Generative Adversarial Nets)
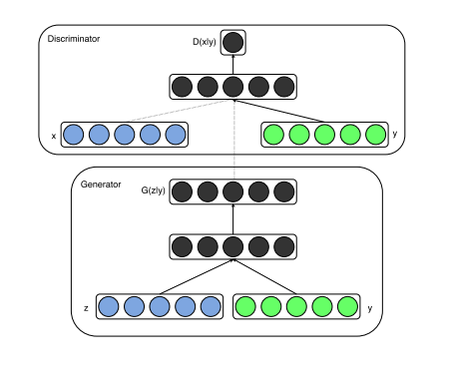
Условные порождающие состязательные сети (англ. Conditional Generative Adversarial Nets, CGAN) $-$ это модифицированная версия алгоритма GAN, которая может быть сконструирована при помощи передачи дополнительных данных y, являющихся условием для генератора и дискриминатора. y может быть любой дополнительной информацией, например, меткой класса, изображением или данными из других моделей, что может позволить контролировать процесс генерации данных. Например, можно подавать параметр y, как условие на класс для генерации чисел, похожих на MNIST. Создание таких картинок, в случае передачи картинки в качетсве y является задачей трансляции изображений. Пример работы CGAN на датасете MNIST с метками классов представленных в виде one-hot векторов [17] (рис. 9).


Как уже было упомянуто на вход генератора и дискримантора из GAN подается дополнительная информация y, например в случае с многослойными перецептронами условие может быть представлено дополнительным входным слоем. (рис. 9) В генераторе априорная вероятность шума и условие комбинируются в объединённое скрытое представление, а состязательная тренирующая модель (Обе сети пытаются оптимизировать целевую функцию или функцию потерь. Когда дискриминатор меняет свое поведение, то и генератор меняет, и наоборот) предоставляет достаточно свободы в том как это представление составляется.[18] В дискриминаторе x и y представлены как входные параметры.
В таком случае задача оптимизации будет выглядеть следующим образом:
В качестве примера использования данного алгоритма можно рассмотреть задачу генерации рукописных цифр.
При создании изображения в генератор поступает скомбинированная информация двух параметров: y и вектора шума. В случае MNIST это может быть, например, просто метка класса (от 0 до 9). На выходе из генератора поступает изображение, полученное с помощью транспонированной свертки (происходит деконволюция). Затем полученное изображение комбинируется с y и поступает в дискриминатор, который в свою очередь применяет свертку, чтобы получить полносвязный слой. Наконец, анализируя полученную информацию (полносвязный слой) дискриминатор принимает решение, является ли изображение сгенерированным. (рис. 12)
Также, используя условные порождающие состязательные сети, можно научить такую сеть генерировать текст по картинке и наоборот. В качестве параметра y в данном случае передается изображение, которое будет описано (рис. 11).
Более того, для такого типа нейронных сетей, принимающих в качестве параметра у некоротое изображение местности, в результате может быть получено аналогичное изображение этого места зимой или летом, днем или ночью. Такая задача является задачей трансляции изображений.
DCGAN (Deep Convolutional Generative Adversarial Nets)
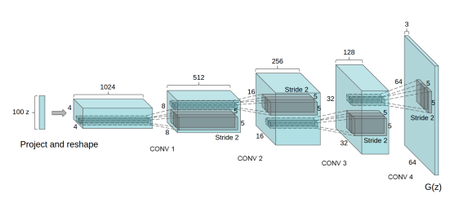
DCGAN $-$ модификация алгоритма GAN, в основе которых лежат сверточные нейронные сети (CNN). Задача поиска удобного представления признаков на больших объемах не размеченных данных является одной из наибольнее активных сфер исследований, в частности представление изображений и видио. Одним из удобных способов поиска представлений может быть DCGAN (рис. 13). Использование сверточных нейронных сетей напрямую не давало хороших результатов, поэтому было внесены ограничения на слои сверток. Эти ограничения и лежат в основе DCGAN:
- Замена всех пулинговых слоев на страйдинговые свертки (strided convolutions) в дискриминаторе и частично-страйдинговые свертки (fractional-strided-convolutions) в генераторе, что позволяет сетям находить подходящие понижения и повышения размерностей;
- Использование батчинговой нормализации для генератора и дискриминатора, то есть нормализация входа так, чтобы среднее значения было равно нулю и дисперсия была равна единице. Не стоит использовать батч-нормализация для выходного слоя генератора и входного дискриминатор.
- Удаление всех полносвязных скрытых уровней для более глубоких архитектур;
- Использование ReLU в качестве функции активации в генераторе для всех слоев, кроме последнего, где используется tanh;
- Использование LeakyReLU в качестве функции активации в дискриминаторе для всех слоев.
Помимо задачи генерации объектов, данный алгоритм хорошо показывает себя в извлечении признаков. Данный алгоритм был натренирован на наборе данных Imagenet-1k[19], после чего были использованы значения со сверточных слоев дискриминатора, подвергнутые max-pooling'у, чтобы образовать матрицы и получить общий вектор признаков на их основе. L2-SVM, c полученным представлением, на наборе данных CIFAR-10[19] превосходит по точности решения, основанные на алгоритме K-Means. Подробнее об этом вы можете прочитать в статье. [20]
StackGAN (Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks)

StackGAN $-$ порождающая состязательная сеть для генерации фото-реалистичных изображений (256x256) исходя из текстового описания. Генерировать фото-реалистичные изображения на обычных GAN сложно, поэтому была придумана двух-этапная модель генерации. Stage-I GAN рисует скетчи с примитивными формами и цветами, основанные на текстовом описании, в низком разрешении. Stage-II GAN принимает на вход изображения с первого этапа и текстовое описание и генерирует изображение в высоком разрешении с фото-реалистичными деталями. Чтобы улучшить разнообразие синтезированных изображений и стабилизировать обучение, вместо CGAN использовался метод Conditioning Augmentation.
Раннее использовались CGAN, поскольку на вход им можно было подавать условия, но просто добавляя слои, увеличивающие размер изображения, достичь хороших результатов не удалось. Поэтому основной задачей было повысить разрешение изображений.
Одной из ключевых особенностей StackGAN является Conditioning Augmentation, так как оно позволило расширить количество примеров тренировочного сета, путем небольших случайных изменений в исходных изображениях, что увеличивало многообразие данных. Как показано на картинке, текстовое описание кодировщиком переводится в векторное представление (рис. 15). Раннее векторное представление нелинейно трансформировалось, чтобы получить скрытые условные переменные, которые подавались на вход генератору, однако простарнство значений скрытых переменных имеет большую размерность, что приводило к разрывам в многообразии данных, что не выгодно для генератора. Чтобы избавиться от этого как раз нужно Conditioning Augmentation, которое в отличии от предоставления фиксированных значений переменных выбирает их из нормального распределения , где среднее значение и ковариация это функции от входного вектора . В добавок к уже упомянотому, чтобы сделать многообразие гладким и не переобучиться, нужно добавить регуляризацию, (KL divergence)[21].
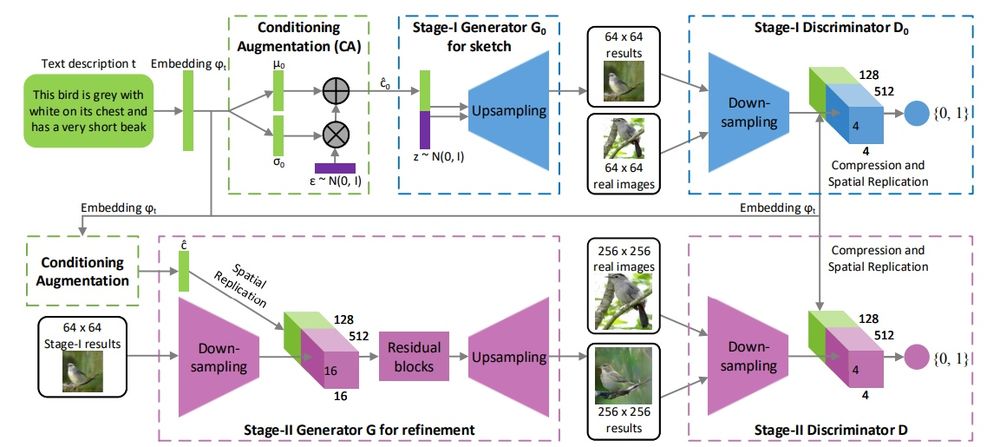
Stage-I GAN тренирует дискриминатор и генератор поочередной максимизицаии и минимизации , как указано в уравенинях:
Где реальное изображение и описание текста берутся из реального распределения данных . шумовой вектор взятого случайно из нормального распределения, параметр регуляризации.
В изображениях с низким разрешенеим, сгенерированные Stage-I GAN, обычно недостает ярких деталей и могут быть искривления форм, некоторые детали изображения также могут быть опущены на первом этапе. Stage-II GAN построен над Stage-I GAN и принимает на вход его выход, и текстовое описание, чтобы исправить и дополнить изображение. Его дискриминатор и генератор тренируются путем поочередной макисимизации и минимизации , как показано в уравнениях:
Где результат работы генератора Stage-I GAN и скрытый параметр подаются на вход дискриминатору и генератору Stage-II GAN, при этом на вход не подается случайное значение, как на первой стадии, поскольку хватает подачи случайного на вход Stage-I GAN. При этом Stage-I GAN и Stage-II GAN имеют разные полно-связные слои, чтобы отличаться по среднему значению и стандартному отклонению, таким образом на разных этапах фокусируюемся на разных деталях исходного текста (рис. 14).
LAPGAN (Laplacian Pyramid of Adversarial Networks)
LAPGAN $-$ генеративная параметрическая модель, представленная пирамидой лапласианов с каскадом сверточных нейронных сетей внутри, которая генерирует изображения постепенно от исходного изображения с низким разрешением к изображению с высоким. На каждом уровне пирамиды обучается сверточная генеративная модель, используя подход порождающих состязательных сетей. Такая стратегия позволяет декомпозировать задачу генерации изображений на последовательность уровней, что упрощает ее решение.
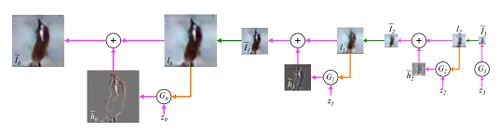
Пирамида лапласианов $-$ это линейное обратимое представление изображений, состоящее из набора частотных полос изображений. Пусть - это операция сжатия изображения размера так, что новое изображение имеет размеры , также - операция расширения такой, что имеет размеры . Тогда пирамида гаусианов имеет вид , где и представляет собой раз выполненное применение . Коэффициенты на каждом уровне пирамиды лапласианов считаются так:
Интуитивно каждый уровень захватывает структуру изображения. Конечный слой пирамиды лапласианов это не разница изображений, а низко-частотное представление равное гаусиану . Реконструкция по пирамиде лапласианов происходит обратным проходом по ней:
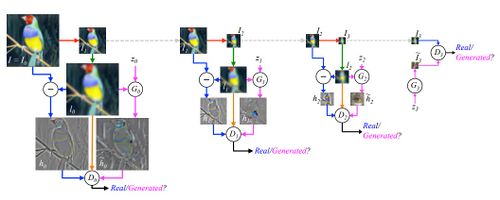
Подход представленный в LAPGAN работает по такому же принципу, только на каждому шаге вместо коэфициентов используются генераторы , каждый из которых захватывает распределение коэфициентов для реальных изображений на разных уровнях пирамиды лапласиана:
Процедура семплинга для нашей модели LAPGAN (рис. 16). Начинаем с шума и используем генеративную модель для создания . Потом расширяем изображение до для следующиего уровня генерации . Вместе с еще одним шумом получаем изображение различия . Продолжаем процесс, пока не получим .
Процедура обучения LAPGAN (рис. 17). Начинаем с изображения размера из тренировчного набора. Берем и сжимаем его(красная стрелка) чтобы получить ; затем расширяем его(зеленая стрелка), чтобы получить низко-частотное изображение ; с равной вероятностью используем его для создния либо реального, либо сгенерированного примера для дискриминатора . В случае реального изображения(синяя стрелка) считаем цветовой контраст , которая подается на вход дискриминатору , для опредления реальное изображение или нет. В случае сгенерированного(розовая стрелка), генеративная сеть получает на вход шум и . Оно генерирует цветовой контраст , который подается на вход . В обоих случаях дискриминатор также получает (оранжевая стрелка). Оптимизируя минмакс игру условной порождающей сети учится генерировать реалистичную высоко-частотную структуру с помощью низко-частотного представления . Такая процедура проходит на всех слоях, кроме последнего, где можно уже использовать обычный GAN.
ControlGAN (Controllable Generative Adversarial Networks)
Контролируемые порождающие состязательные сети (англ. Controllable Generative Adversarial Nets, ControlGAN) $-$ модифицированная версия алгоритма GAN, состоящая из трех нейронных сетей: генератор, дискриминатор, классификатор. Концепт модели ControlGAN (рис. 18). Как и в обычной версии алгоритма, генератор пытается обмануть дискриминатор, и одновременно с этим пытается быть классифицированным как нужный класс в классификаторе.
Хоть CGAN и являются самыми популярными моделями для генерации образцов, зависимых от внешних данных, но лучше они умеют генерировать образцы с заданными ярко отличительными чертами (цвет волос, веснушки), но менее явные детали (форма бровей, сережки) вызывают затруднения (Но более поздний StyleGAN2 справляется и с этой задачей). C помощью отделения классификатора от дискриминатора, ControlGAN позволяет контролировать черты образцов. К тому же и само качество сгенерированных изображений может быть улучшено засчет того, что такое разделение на три составляющие дает возможность дискриминатору лучше выполнять свою главную задачу.
Более того, аугментация данных может помешать некоторым сетям, например, Auxiliary Classifier GAN (ACGAN) обучаться, хотя сам способ может улучшить качество классификации. К тому же в случае контролируемой генерации нет необходимости размечать тренировочные данные, выбираются желаемые характеристики объектов для генерации, а не условная информация (например, метка объекта).
Иллюстрация принципа работы сети (рис. 19). Зеленые линии $-$ результат работы классификатора; оранжевые $-$ дискриминатора. Серые фигуры $-$ образцы из разных классов. Результат генератора обозначается голубыми участками, которыми он показывает распределение образцов, как и пытается быть классифицированным верно.
ControlGAN минимизирует следующие уравнения:
,
,
.
$-$ метка для генератора, $-$ параметр для дискриминатора, $-$ параметр для входных меток на генератор, $-$ метки образца .
$-$ отношение между ошибками классификации сгенерированных образцов и изначальных данных. Для тренировки генератора используем оценочное значение , полученное, использующее классификатор и генератор из сети. При значении меньше $1$, генератор обучается на входных данных, иначе обучается генерировать образцы. С помощью этого параметра ControlGAN управляет, чему из вышеперечисленного обучаться. Сам параметр поддерживает постоянной отношение между ошибками.
,
,
$-$ коэффициент обучения для .
См. также
Примечания
- ↑ How to Train a GAN? Tips and tricks to make GANs work
- ↑ Common Problems
- ↑ [https://research.nvidia.com/sites/default/files/pubs/2017-10_Progressive-Growing-of/karras2018iclr-paper.pdf PROGRESSIVE GROWING OF GANS FOR IMPROVED QUALITY, STABILITY, AND VARIATION]
- ↑ Shane Barratt, Rishi Sharma — A Note on the Inception Score
- ↑ Frechet Inception distance on Wikipedia
- ↑ Yazeed Alharbi, Peter Wonka — Disentangled Image Generation Through Structured Noise Injection, 3.3
- ↑ Yazeed Alharbi, Peter Wonka — Disentangled Image Generation Through Structured Noise Injection, 3.5
- ↑ Augustus Odena — Conditional Image Synthesis with Auxiliary Classifier GANs
- ↑ Takeru Miyato — SPECTRAL NORMALIZATION FOR GENERATIVE ADVERSARIAL NETWORKS
- ↑ Han Zhang — Self-Attention Generative Adversarial Networks
- ↑ Andrew Brock — LARGE SCALE GAN TRAINING FOR HIGH FIDELITY NATURAL IMAGE SYNTHESIS
- ↑ Jun-Yan Zhu & Taesung Park — Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
- ↑ Christian Ledig — Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
- ↑ Phillip Isola — Image-to-Image Translation with Conditional Adversarial Nets
- ↑ Han Zhang — StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks
- ↑ Li-Chia Yang — MIDINET: A CONVOLUTIONAL GENERATIVE ADVERSARIAL NETWORK FOR SYMBOLIC-DOMAIN MUSIC GENERATION
- ↑ CGAN
- ↑ Yoshua Bengio, Gre ́goire Mesnil, Yann Dauphin and Salah Rifai — Better Mixing via Deep Representations
- ↑ 19,0 19,1 Известные наборы данных
- ↑ Alec Radford, Luke Metz, Soumith Chintala — Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks
- ↑ Kullback-Leibler divergence
Источники информации
- Сергей Николенко, Артур Кадурин, Екатерина Архангельская. Глубокое обучение. Погружение в мир нейронных сетей. — «Питер», 2018. — С. 348-360.
- Medium | GAN — Why it is so hard to train Generative Adversarial Networks!
- CGAN Paper
- DCGAN Paper
- StackGAN Paper
- LAPGAN Paper
- ControlGAN Paper
- Interpreting the Latent Space Paper