Heavy-light декомпозиция — различия между версиями
| Строка 1: | Строка 1: | ||
'''Heavy-light декомпозиция''' {{---}} техника разбиения дерева на множество рёберно-непересекающихся путей так, чтобы при прохождении от одной вершины до другой произошла смена не более, чем <tex>O(\log{n})</tex> путей. | '''Heavy-light декомпозиция''' {{---}} техника разбиения дерева на множество рёберно-непересекающихся путей так, чтобы при прохождении от одной вершины до другой произошла смена не более, чем <tex>O(\log{n})</tex> путей. | ||
==Описание задачи== | ==Описание задачи== | ||
| − | Пусть у нас есть дерево <tex>T</tex> c <tex>n</tex> вершинами и нам нужно проводить операции на нем на пути от вершины <tex>v</tex> до вершины <tex>u</tex>. Множество подобных запросов делаются за время <tex>O(\log^p{n})</tex> | + | Пусть у нас есть дерево <tex>T</tex> c <tex>n</tex> вершинами и нам нужно проводить операции на нем на пути от вершины <tex>v</tex> до вершины <tex>u</tex>. Множество подобных запросов делаются за время <tex>O(\log^p{n})</tex> с помощью Heavy-light декомпозиции. |
==Описание декомпозиции== | ==Описание декомпозиции== | ||
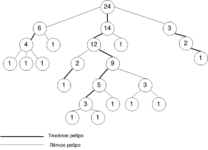
[[Файл:Heavylight.png|thumb|right|300x150px|Пример разбиения на лёгкие/тяжёлые рёбра.]] | [[Файл:Heavylight.png|thumb|right|300x150px|Пример разбиения на лёгкие/тяжёлые рёбра.]] | ||
Версия 15:24, 7 июня 2015
Heavy-light декомпозиция — техника разбиения дерева на множество рёберно-непересекающихся путей так, чтобы при прохождении от одной вершины до другой произошла смена не более, чем путей.
Содержание
Описание задачи
Пусть у нас есть дерево c вершинами и нам нужно проводить операции на нем на пути от вершины до вершины . Множество подобных запросов делаются за время с помощью Heavy-light декомпозиции.
Описание декомпозиции
Декомпозиция заключается в классификации всех рёбер дерева в 2 вида: легкие и тяжёлые. Введём функцию , которая будет обозначать размер поддерева вершины .
Тяжёлые ребра — ребра такие, что .
Лёгкие ребра — соответственно все остальные.
Очевидно, что из вершины может выходить как максимум одно тяжёлое ребро, т.к. иначе у нас есть два поддерева по как минимум вершин, а также сама вершина . Итого вершин, тогда как у нас всего вершин в поддереве.
Теперь рассмотрим вершины, из которых не ведет ни одно тяжёлое ребро. Будем идти от них вверх до корня или пока не пройдем легкое ребро. Получится какое-то множество путей. Утверждается, что оно будет являться искомым.
Доказательство корректности полученной декомпозиции
| Утверждение: |
Полученная декомпозиция является искомой. |
|
Докажем по отдельности корректность декомпозиции. 1. Все рёбра покрыты путями. Есть два типа вершин: те, из которых ведёт ровно одно тяжёлое ребро и те, из которых не ведёт ни одного тяжёлого ребра. Для первого типа вершин мы дойдем до них некоторым путём через тяжёлое ребро снизу по определению выбора путей, а лёгкие рёбра ведущие из неё возьмем как последние рёбра в соответствующих путях. Для второго типа вершин мы по определению выбора путей возьмем их как начальные и пойдем вверх. Таким образом все рёбра будут покрыты. 2. Все пути не пересекаются. Докажем от противного. Пусть мы взяли какое-то ребро дважды. Это значит, что из какой-то вершины вело более чем одно тяжёлое ребро, чего быть не могло. Получили противоречие. 3. При прохождении пути от вершины до вершины произойдет смена не более, чем путей. Докажем эквивалентный факт, что при пути от любой вершины до корня мы сменим не более, чем путей. Рассмотрим лёгкое ребро. Заметим, что проход вниз по такому ребру уменьшает размер поддерева как минимум в 2 раза. Но смена пути может произойти только при переходе по лёгкому ребру. Таким образом мы сменим не более путей. |
Применение
Сумма на пути
Классическая задача о сумме на пути в дереве с решается с помощью Heavy-light декомпозиции за время. Возможны модификации веса.
Построим дерево отрезков над каждым путём. Рассмотрим запрос . Давайте найдем вершину , которая является (например с помощью двоичного подъема. Мы разбили запрос на два: и , на каждый из которых можно легко ответить выбирая путь, содержащий самую нижнюю вершину и вырезать его, пока этот путь не содержит .
Так мы сможем получать ответ на пути за . А всего таких путей нужно будет рассмотреть . Итого мы способны решить эту задачу за время .
Хоть это и не самый эффективный способ для решения этой задачи, но можно заметить, что с помощью такого трюка мы можем решить широкий класс задач просто сведя её к задаче о запросах в дереве отрезков (такие как максимум на пути, покраска на пути, прибавление на пути и др.).
Реализация
Здесь будет простая реализация Heavy-light декомпозиции