Link-Cut Tree — различия между версиями
Lena (обсуждение | вклад) (→Решение задачи в частном случае) |
Lena (обсуждение | вклад) (→Решение задачи в частном случае) |
||
| Строка 6: | Строка 6: | ||
==Решение задачи в частном случае== | ==Решение задачи в частном случае== | ||
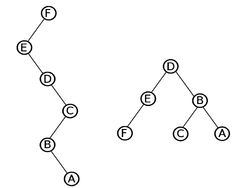
| − | Сначала научимся выполнять эти операции для частного случая, в котором все деревья - это пути. Для этого представим путь в виде splay-дерева, в которм ключи выбираются равными глубине вершины. | + | Сначала научимся выполнять эти операции для частного случая, в котором все деревья - это пути. Для этого представим путь в виде splay-дерева, в которм ключи выбираются равными глубине вершины. [[Файл:Path_to_tree.png|250px|thumb|right|Пример построения дерева для пути]] |
| − | [[Файл:Path_to_tree.png|250px|thumb|right|Пример построения дерева для пути]] | ||
Тогда операциям link и cut будут соответсвовать merge и split. | Тогда операциям link и cut будут соответсвовать merge и split. | ||
| Строка 14: | Строка 13: | ||
сумма | сумма | ||
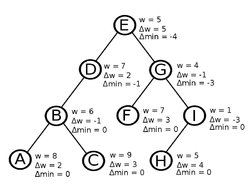
| − | + | При прибавлении <tex>\alpha</tex> на пути от вершины <tex>v</tex> до корня, сначала вызвается <tex>splay(v)</tex>, после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить <tex>\alpha</tex> к <tex>\Delta w(v)</tex> и ,чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть <tex>\alpha</tex> от <tex>\Delta w(v.right)</tex>. | |
| − | [[Файл:Linkcut_weights.png|250px|thumb|right| | + | [[Файл:Linkcut_weights.png|250px|thumb|right|]] |
Для поиска минимума поступим аналогично. Определим <tex>\Delta min(v)</tex> таким образом, чтобы сохранялся следующий инвариант: <tex>min(v) = \Delta min(v) + w(v) </tex>. Пусть <tex>l</tex> и <tex>r</tex> дети <tex>v</tex>, тогда | Для поиска минимума поступим аналогично. Определим <tex>\Delta min(v)</tex> таким образом, чтобы сохранялся следующий инвариант: <tex>min(v) = \Delta min(v) + w(v) </tex>. Пусть <tex>l</tex> и <tex>r</tex> дети <tex>v</tex>, тогда | ||
| Строка 27: | Строка 26: | ||
Чтобы найти минимум на пути, надо вызвать <tex>splay(v)</tex>, а затем сравнить минимум <tex>v</tex> и минимум её левого ребенка. | Чтобы найти минимум на пути, надо вызвать <tex>splay(v)</tex>, а затем сравнить минимум <tex>v</tex> и минимум её левого ребенка. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Link-cut tree== | ||
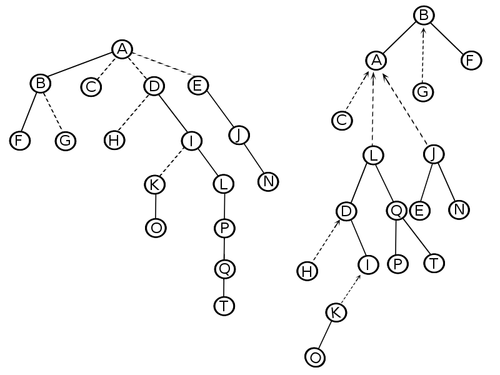
| + | Чтобы обобщить, разобъем дерево на множество непересекающихся путей. Каждое ребро обозначим либо solid-ребром, либо dashed-ребром. Все пути в представляемом дереве хранятся в виде splay-деревьев. Корень каждого splay-дерева хранит указатель на вершину-родителя. | ||
| + | [[Файл:Linkcut_paths.png|500px||center|Разбиение дерева на пути]] | ||
| + | |||
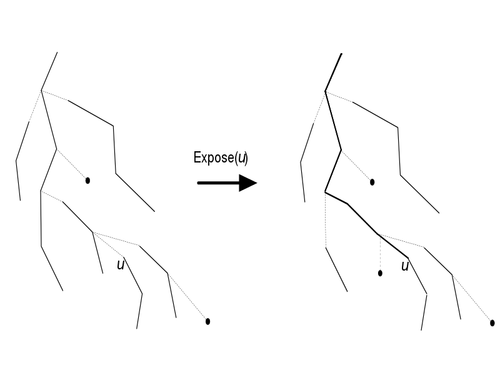
| + | Ключевая операция в link-cut-деревьях {{---}} <tex>expose(u)</tex>. После её выполнения <tex>u</tex> лежит на одном пути с корнем представляемого дерева и при этом становится корнем в splay-дереве получившегося пути. | ||
| + | [[Файл:Linkcut_expose.png|500px||center|Разбиение дерева на пути]] | ||
Версия 23:34, 8 июня 2014
Link-cut tree — это структура данных, которая хранит лес деревьев и позволяет выполнять следующие операции:
- искать минимум на пути от вершины до корня;
- прибавлять константу на пути от вершины до корня;
- link(u,w) -- подвешивать одно дерево на другое;
- cut(v) -- отрезать дерево с корнем в вершине v.
Решение задачи в частном случае
Сначала научимся выполнять эти операции для частного случая, в котором все деревья - это пути. Для этого представим путь в виде splay-дерева, в которм ключи выбираются равными глубине вершины.Тогда операциям link и cut будут соответсвовать merge и split.
Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить велечину , которая равна разнице между весом вершины и весом её ролителя. Для корня это значение равно весу самого корня. Поэтому вес вершины определятся следующим образом:
сумма
При прибавлении на пути от вершины до корня, сначала вызвается , после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить к и ,чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть от .
Для поиска минимума поступим аналогично. Определим таким образом, чтобы сохранялся следующий инвариант: . Пусть и дети , тогда
Чтобы найти минимум на пути, надо вызвать , а затем сравнить минимум и минимум её левого ребенка.
Link-cut tree
Чтобы обобщить, разобъем дерево на множество непересекающихся путей. Каждое ребро обозначим либо solid-ребром, либо dashed-ребром. Все пути в представляемом дереве хранятся в виде splay-деревьев. Корень каждого splay-дерева хранит указатель на вершину-родителя.
Ключевая операция в link-cut-деревьях — . После её выполнения лежит на одном пути с корнем представляемого дерева и при этом становится корнем в splay-дереве получившегося пути.