NP-полнота задачи о независимом множестве — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(создание странички)
 
м (ё)
(не показаны 23 промежуточные версии 2 участников)
Строка 1: Строка 1:
 
==Формулировка==
 
==Формулировка==
−
Пусть задан неориентированный граф <math>G</math> и натуральное число <math>k</math>. '''Задача о независимом множестве(IND)''' решает вопрос о том, содержит ли граф <math>G</math> подграф <math>H</math> размером <math>k</math>, никакая пара вершин в котором не соединена ребром.
+
Языком IND называют множество пар <tex>\langle G,k \rangle</tex>, где <math>G</math> - неориентированный граф, <math>k</math> - натуральное число. Слово принадлежит языку IND, если граф <math>G</math> содержит подграф <math>H</math> размером <math>k</math>, никакая пара вершин в котором не соединена ребром. Задача о независимом множестве является [[Понятие NP-трудной и NP-полной задачи|NP-полной]].
 +
 
 
==Доказательство NP-полноты==
 
==Доказательство NP-полноты==
 
Для доказательства NP-полноты задачи о независимом множестве покажем, что она является NP-трудной и принадлежит классу NP.
 
Для доказательства NP-полноты задачи о независимом множестве покажем, что она является NP-трудной и принадлежит классу NP.
 
===Задача о независимом множестве является NP-трудной===
 
===Задача о независимом множестве является NP-трудной===
−
Для доказательства этого сведем задачу <math>3-SAT</math> к нашей:  
+
Для доказательства этого [[Сведение по Карпу|сведем по Карпу]] задачу <math>3SAT</math> к нашей:  
 +
 
 +
<math>3SAT \le_{k} IND</math>
  
−
<math>3-SAT \le IND</math>
+
Пусть задана булева формула в <math>3SAT</math>, в которой <math>k</math> скобок. Построим для неё соответствующий граф. Для каждой скобки нарисуем три вершины, соединим их попарно рёбрами и подпишем их именами соответствующих литералов. Так же соединим рёбрами пары вершин вида <math>x,\neg x</math>.
  
−
Пусть задана булева формула в <math>3-SAT</math>, в которой <math>k</math> скобок. Построим для нее соответствующий граф. Для каждой скобки нарисуем три вершины, соединим их попарно ребрами и подпишем их именами соответствующих переменных. Так же соединим ребрами пары вершин вида <math>x,\overline{x}</math>.
+
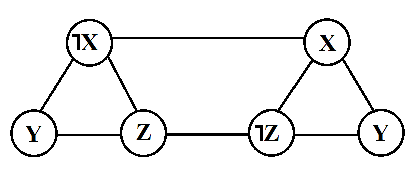
<math>(\neg x\lor y\lor z)\land (x \lor y \lor \neg z) \to</math>[[Файл:IND_GRAPH.png]]
  
−
<math>(\overline{x}\lor y\lor z)\land (x \lor y \lor \overline{z}) \to</math>[[Файл:Example.jpg]]
+
Докажем, что формула выполнима тогда и только тогда, когда в соответствующем графе есть независимое множество из <math>k</math> вершин. Пусть формула выполнима, тогда в каждой скобке есть хотя бы один литерал, принимающий значение “истина”. Выберем соответствующую ему вершину в графе. Полученное множество вершин является независимым, так как рёбрами соединены только те вершины, которые соответствуют литералам из одной скобки (а мы выбирали только один литерал из каждой скобки), а так же вершины вида <math>x,\neg x</math>, соответствующие литералы которых не могут одновременно принимать значение “истина”. Пусть теперь в графе есть независимое множество, размера <math>k</math>. Тогда в каждой тройке вершин, соответствующих некоторой скобке, выбрана ровно одна вершина. Установим значение соответствующего литерала “истина”. Это можно сделать, так как нет рёбер между вершинами вида <math>x,\neg x</math>. Тогда в каждой скобке, будет хотя бы один литерал, имеющий значение “истина”, значит вся формула будет принимать значение “истина”. Построение по формуле соответствующего графа можно сделать за полиномиальное время.
  
−
Докажем, что формула выполнима тогда и только тогда, когда в соответствующем графе есть независимое множество из <math>k</math> вершин. Пусть формула выполнима, тогда в каждой скобке есть хотя бы одна переменная, принимающая значение “правда”. Выберем соответствующую переменную в качестве вершины в графе. Выбранное множество вершин является независимым, так как ребрами соединены только вершины, которые соответствуют переменным из одной скобки(а мы выбирали только одну переменную из каждой скобки) и пары вершин, которым советуют пары переменных вида <math>x,\overline{x}</math>, которые не могут одновременно принимать значение “правда”. Пусть в графе есть независимое множество, размера <math>k</math>. Тогда в каждой тройке вершин, соответствующих некоторой скобке, выбрана ровно одна вершина. Установим значение соответствующей переменной “правда”. Тогда в каждой скобке, будет хотя бы одна переменная, имеющая значение “правда”, значит вся формула будет принимать значение “правда”. Построение по формуле соответствующего графа можно сделать за полиномиальное время.
 
 
===Задача о независимом множестве принадлежит классу NP===
 
===Задача о независимом множестве принадлежит классу NP===
 
В качестве сертификата возьмем набор из <math>k</math> вершин. За время <math>O(k^2)</math> можно проверить, является ли данное множество вершин независимым.
 
В качестве сертификата возьмем набор из <math>k</math> вершин. За время <math>O(k^2)</math> можно проверить, является ли данное множество вершин независимым.

Версия 00:06, 31 января 2017

Формулировка

Языком IND называют множество пар [math]\langle G,k \rangle[/math], где [math]G[/math] - неориентированный граф, [math]k[/math] - натуральное число. Слово принадлежит языку IND, если граф [math]G[/math] содержит подграф [math]H[/math] размером [math]k[/math], никакая пара вершин в котором не соединена ребром. Задача о независимом множестве является NP-полной.

Доказательство NP-полноты

Для доказательства NP-полноты задачи о независимом множестве покажем, что она является NP-трудной и принадлежит классу NP.

Задача о независимом множестве является NP-трудной

Для доказательства этого сведем по Карпу задачу [math]3SAT[/math] к нашей:

[math]3SAT \le_{k} IND[/math]

Пусть задана булева формула в [math]3SAT[/math], в которой [math]k[/math] скобок. Построим для неё соответствующий граф. Для каждой скобки нарисуем три вершины, соединим их попарно рёбрами и подпишем их именами соответствующих литералов. Так же соединим рёбрами пары вершин вида [math]x,\neg x[/math].

[math](\neg x\lor y\lor z)\land (x \lor y \lor \neg z) \to[/math]IND GRAPH.png

Докажем, что формула выполнима тогда и только тогда, когда в соответствующем графе есть независимое множество из [math]k[/math] вершин. Пусть формула выполнима, тогда в каждой скобке есть хотя бы один литерал, принимающий значение “истина”. Выберем соответствующую ему вершину в графе. Полученное множество вершин является независимым, так как рёбрами соединены только те вершины, которые соответствуют литералам из одной скобки (а мы выбирали только один литерал из каждой скобки), а так же вершины вида [math]x,\neg x[/math], соответствующие литералы которых не могут одновременно принимать значение “истина”. Пусть теперь в графе есть независимое множество, размера [math]k[/math]. Тогда в каждой тройке вершин, соответствующих некоторой скобке, выбрана ровно одна вершина. Установим значение соответствующего литерала “истина”. Это можно сделать, так как нет рёбер между вершинами вида [math]x,\neg x[/math]. Тогда в каждой скобке, будет хотя бы один литерал, имеющий значение “истина”, значит вся формула будет принимать значение “истина”. Построение по формуле соответствующего графа можно сделать за полиномиальное время.

Задача о независимом множестве принадлежит классу NP

В качестве сертификата возьмем набор из [math]k[/math] вершин. За время [math]O(k^2)[/math] можно проверить, является ли данное множество вершин независимым.

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=NP-полнота_задачи_о_независимом_множестве&oldid=60356»