NP-полнота задачи о раскраске графа — различия между версиями
Alant (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 30 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
== Формулировка задачи== | == Формулировка задачи== | ||
| − | Даны граф < | + | Даны граф <tex> G = \langle V, E \rangle </tex> и число <tex> k </tex>. Необходимо проверить, правда ли, что можно раскрасить вершины графа в <tex> k </tex> цветов так, чтобы любые две вершины, соединённые ребром, имели разные цвета. |
== Утверждение == | == Утверждение == | ||
| − | Сформулированная выше задача NP-полна. | + | Сформулированная выше задача [[NP-полнота|NP-полна]]. |
== Доказательство == | == Доказательство == | ||
=== Доказательство принадлежности задачи классу NP === | === Доказательство принадлежности задачи классу NP === | ||
| − | Сертификатом для решения данной задачи будет последовательность < | + | Сертификатом для решения данной задачи будет последовательность <tex> \{c_i\}_ {i=1}^{n}</tex>, где <tex> n = |V| </tex>, а <tex> c_i </tex> обозначает цвет <tex>i</tex>-ой вершины. Проверку корректности такого сертификата легко осуществить за полиномиальное время, например, перебором всех пар вершин и проверкой того, что в случае, когда они соединены ребром, они имеют разные цвета, лежащие на отрезке <tex> [1, k] </tex>. С другой стороны, очевидно, что если задача имеет решение, то такой сертификат существует. |
=== Доказательство принадлежности задачи классу NPH === | === Доказательство принадлежности задачи классу NPH === | ||
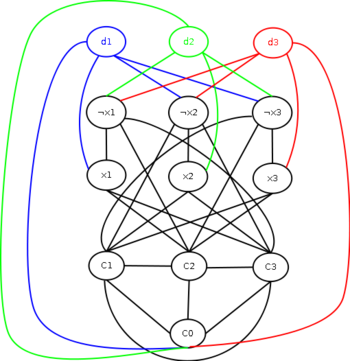
| − | Сведем задачу 3CNFSAT к данной.<br/> | + | [[Файл:3cnfsat.png|thumb|350px|Граф, построенный по формуле <tex refresh dpi=100> (x_1 \lor \lnot x_2 \lor \lnot x_3) \land (\lnot x_1 \lor x_2 \lor \lnot x_3) \land (\lnot x_1 \lor \lnot x_2 \lor x_3)</tex>]] |
| − | Пусть дана < | + | Сведем задачу [[3CNFSAT]] к данной.<br/> |
| − | # Ровно одно выражение из < | + | Пусть дана формула <tex> \varphi = (a_1 \lor b_1 \lor c_1) \land (a_2 \lor b_2 \lor c_2) \land ... \land (a_m \lor b_m \lor c_m) </tex>, где <tex>a_i</tex>, <tex>b_i</tex> и <tex>c_i</tex> — переменные или их отрицания (возможно, с повторениями). Сами переменные будем обозначать <tex> \{x_i\}_{i=1}^n </tex>.<br/> Заметим следующие тривиальные факты, которые будут использованы при построении графа: |
| − | # < | + | # Ровно одно выражение из <tex> \{x_i, \lnot {x_i}\} </tex> истинно; |
| − | Построим множества V и E будущего графа | + | # <tex> \varphi \in 3CNFSAT </tex> тогда и только тогда, когда существует набор, обращающий каждую скобку в истину. |
| − | * < | + | Построим множества V и E будущего графа следующим образом: |
| − | * < | + | * <tex> V = \{c_i\}_{i=0}^n </tex>; |
| − | Будем интерпретировать < | + | * <tex> E = \{\langle c_i, c_j \rangle \}_{i,j=0, i \ne j}^n </tex>. |
| − | * < | + | Будем интерпретировать <tex> c_i </tex> как цвет (соотвественно, вершина <tex> c_i </tex> всегда покрашена в цвет <tex> c_i </tex>), причем <tex>c_0</tex> — цвет, обозначающий истину, а все остальные цвета означают ложь). |
| − | * | + | * Для всех <tex> i \in \{1 .. n\} </tex> добавим в V вершины <tex> v_i, \tilde{v_i} </tex>, отвечающие <tex> x_i </tex> и <tex> \lnot {x_i} </tex> соответственно, и соединим каждую такую пару ребром; |
| − | Осталось сделать так, чтобы возможность сделать истинной каждую скобку соответствовала необходимости покрасить хотя бы одну из вершин, соответствующих переменным в ней, в цвет < | + | * Каждую вершину из <tex> \{v_i, \tilde{v_i}\} </tex> соединим рёбрами со всеми <tex> c_j </tex>, кроме <tex> c_0 </tex> и <tex> c_i </tex>. |
| + | Этим мы обеспечили выполнение первого условия из приведённых выше, так как теперь ровно одна вершина из <tex> \{v_i, \tilde{v_i}\} </tex> окрашена в цвет <tex> c_0 </tex>, а другая — в цвет <tex> c_i </tex>. <br/> | ||
| + | Осталось сделать так, чтобы возможность сделать истинной каждую скобку соответствовала необходимости покрасить хотя бы одну из вершин, соответствующих переменным в ней, в цвет <tex> c_0 </tex>. | ||
| + | * Для этого для каждой скобки вида <tex> ([\lnot]x_i \lor [\lnot] x_j \lor [\lnot] x_k)_l </tex> добавим вершину <tex> d_l </tex>, соединив её с соответствующими <tex> v_i (\tilde{v_i}), v_j(\tilde{v_j}), v_k(\tilde{v_k}) </tex>, а также со всеми <tex> c_i </tex>, кроме <tex> c_i, c_j, c_k </tex>. Тем самым, <tex> d_l </tex> «не даёт» покрасить все три вершины, отвечающие термам в скобке, в «ложный» цвет (напомним, что все цвета, кроме <tex> c_0 </tex>, мы условились называть «ложными»).<br/> | ||
| + | ==== Доказательство корректности сведения ==== | ||
| + | Покажем теперь, что такой граф будет <tex>(n+1)</tex>-раскрашиваемым тогда и только тогда, когда исходная формула принадлежит <tex> 3CNFSAT </tex>. | ||
| + | # <tex> \Rightarrow </tex>. Из построения ясно, что можно покрасить вершины полученного графа, соответствующие истинным термам набора, обращающего формулу в истину, в цвет <tex>c_0</tex>, а вершины, соответствующие ложным термам, — в соответствующие "ложные" цвета. | ||
| + | # <tex> \Leftarrow </tex>. Построим по раскраске графа набор переменных <tex> \{x_i\}_{i=1}^n </tex>, в котором <tex> x_i </tex> истинно тогда и только тогда, когда <tex> v_i </tex> покрашена в цвет <tex> c_0 </tex>. Этот набор непротиворечив (мы не попытались одну и ту же переменную сделать и истинной, и ложной одновременно). Он также обращает формулу в истинную, так как по постронию в каждой скобке есть хотя бы один истинный терм. | ||
| + | |||
| + | [[Категория:NP]] | ||
| + | [[Категория:Раскраски графов]] | ||
Текущая версия на 19:04, 4 сентября 2022
Содержание
Формулировка задачи
Даны граф и число . Необходимо проверить, правда ли, что можно раскрасить вершины графа в цветов так, чтобы любые две вершины, соединённые ребром, имели разные цвета.
Утверждение
Сформулированная выше задача NP-полна.
Доказательство
Доказательство принадлежности задачи классу NP
Сертификатом для решения данной задачи будет последовательность , где , а обозначает цвет -ой вершины. Проверку корректности такого сертификата легко осуществить за полиномиальное время, например, перебором всех пар вершин и проверкой того, что в случае, когда они соединены ребром, они имеют разные цвета, лежащие на отрезке . С другой стороны, очевидно, что если задача имеет решение, то такой сертификат существует.
Доказательство принадлежности задачи классу NPH
Сведем задачу 3CNFSAT к данной.
Пусть дана формула , где , и — переменные или их отрицания (возможно, с повторениями). Сами переменные будем обозначать .
Заметим следующие тривиальные факты, которые будут использованы при построении графа:
- Ровно одно выражение из истинно;
- тогда и только тогда, когда существует набор, обращающий каждую скобку в истину.
Построим множества V и E будущего графа следующим образом:
- ;
- .
Будем интерпретировать как цвет (соотвественно, вершина всегда покрашена в цвет ), причем — цвет, обозначающий истину, а все остальные цвета означают ложь).
- Для всех добавим в V вершины , отвечающие и соответственно, и соединим каждую такую пару ребром;
- Каждую вершину из соединим рёбрами со всеми , кроме и .
Этим мы обеспечили выполнение первого условия из приведённых выше, так как теперь ровно одна вершина из окрашена в цвет , а другая — в цвет .
Осталось сделать так, чтобы возможность сделать истинной каждую скобку соответствовала необходимости покрасить хотя бы одну из вершин, соответствующих переменным в ней, в цвет .
- Для этого для каждой скобки вида добавим вершину , соединив её с соответствующими , а также со всеми , кроме . Тем самым, «не даёт» покрасить все три вершины, отвечающие термам в скобке, в «ложный» цвет (напомним, что все цвета, кроме , мы условились называть «ложными»).
Доказательство корректности сведения
Покажем теперь, что такой граф будет -раскрашиваемым тогда и только тогда, когда исходная формула принадлежит .
- . Из построения ясно, что можно покрасить вершины полученного графа, соответствующие истинным термам набора, обращающего формулу в истину, в цвет , а вершины, соответствующие ложным термам, — в соответствующие "ложные" цвета.
- . Построим по раскраске графа набор переменных , в котором истинно тогда и только тогда, когда покрашена в цвет . Этот набор непротиворечив (мы не попытались одну и ту же переменную сделать и истинной, и ложной одновременно). Он также обращает формулу в истинную, так как по постронию в каждой скобке есть хотя бы один истинный терм.