QpmtnCmax — различия между версиями
(правки) |
|||
| Строка 1: | Строка 1: | ||
| − | = | + | <tex dpi = "200">Q \mid pmtn \mid C_{max}</tex> |
| − | + | {{Задача | |
| + | |definition= | ||
| + | Дано несколько станков с разной скоростью выполнения работ, работающих параллельно. Работа может быть прервана в любой момент и продолжена позже на любой машине. Необходимо минимизировать время выполнения всех работ. | ||
| + | }} | ||
| − | + | ===Алгоритм построения расписания=== | |
| + | Перед выполнением алгоритма, упорядочим все работы по убыванию их времени выполнения:<tex> p_1 \geqslant p_2 \geqslant p_3 \ldots </tex>, а все машины в порядке убывания скоростей: <tex> s_1 \geqslant s_2 \geqslant s_3 \ldots </tex>. Введем следующие обозначения: | ||
| − | + | <tex> P_i = p_1 + \ldots + p_i</tex> | |
| − | + | <tex> S_j = s_1 + \ldots + s_j</tex> | |
| − | + | <tex>i = 1 \ldots n</tex>, <tex>j = 1 \ldots m</tex>, <tex> p_i</tex> - время выполнения <tex>i</tex>-ой работы, <tex> s_j</tex> - скорость работы <tex> j </tex>-oй машины. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <tex>i = 1 | ||
Необходимое условие для выполнения всех работ в интервале <tex>[0..T]</tex>: | Необходимое условие для выполнения всех работ в интервале <tex>[0..T]</tex>: | ||
| − | <tex> P_n = p_1 + | + | <tex> P_n = p_1 + \ldots + p_n \leqslant s_1T + \ldots + s_mT = S_mT</tex> или <tex>P_n/S_m \leqslant T</tex> |
| − | Кроме того, должно выполняться условие <tex>P_j/S_j \ | + | Кроме того, должно выполняться условие <tex>P_j/S_j \leqslant T</tex> для всех <tex> j = 1 \ldots m - 1 </tex>, так как это нижняя оценка времени выполнения работ <tex> J_1 \ldots J_j</tex>. Исходя из этого получаем нижнюю границу <tex>C_{max}</tex> : |
<tex>C_{max}</tex> = <tex>\max\{\max\limits_{j=1}^{m-1} {P_j \over S_j}, {P_n \over S_m}\}</tex> | <tex>C_{max}</tex> = <tex>\max\{\max\limits_{j=1}^{m-1} {P_j \over S_j}, {P_n \over S_m}\}</tex> | ||
| Строка 32: | Строка 29: | ||
<tex>t \leftarrow 0 </tex> | <tex>t \leftarrow 0 </tex> | ||
| − | ''' | + | '''while''' <tex>\exists p(t) > 0</tex> |
Assign(t) | Assign(t) | ||
| − | <tex> | + | <tex>t_1 \leftarrow \min (s \mid s > t </tex> '''and''' <tex>p(s) = 0)</tex> |
| − | <tex> | + | <tex>t_2 \leftarrow \min (s \mid s > t</tex> '''and''' <tex>\exists i</tex>, <tex>j : p_i(t) > p_j(t)</tex> '''and''' <tex>p_i(s) = p_j(s))</tex> |
| − | <tex> t \leftarrow \min( | + | <tex>t \leftarrow \min(t_1</tex>, <tex>t_2)</tex> <font color=green> // поиск следующего момента времени, в который нужно будет перераспределить машины/работы </font> |
Построение расписания | Построение расписания | ||
Функция <tex>Assign(t)</tex>: | Функция <tex>Assign(t)</tex>: | ||
| − | <tex>J </tex> | + | <tex>J = \{i \mid p_i(t) > 0\}</tex> <font color=green> // множество работ с положительным level </font> |
| − | <tex>M = \{M_1 | + | <tex>M = \{M_1 \ldots M_m\}</tex> <font color=green> // множество всех станков </font> |
| − | ''' | + | '''while''' <tex>J \ne \varnothing</tex> '''or''' <tex>M \ne \varnothing</tex> |
| − | + | max <font color=green> // максимальное значение level из J </font> | |
| − | <tex>r | + | count <font color=green> // количество работ с level = max </font> |
| − | + | <tex>r = min(|M|</tex>, <tex>count)</tex> | |
| − | <tex>J \leftarrow J | + | <tex>I \leftarrow \{r</tex> работ из <tex>J \mid p(t) = max\}</tex> |
| − | + | <tex>M' \leftarrow \{r</tex> самых быстрых машин из <tex>M\}</tex> | |
| + | Распределяем работы | ||
| + | <tex>J \leftarrow J \setminus I</tex> | ||
| + | <tex>M \leftarrow M \setminus M'</tex> | ||
| − | ==Доказательство корректности алгоритма== | + | ===Доказательство корректности алгоритма=== |
Так как нижняя граница <tex>C_{max}</tex>: | Так как нижняя граница <tex>C_{max}</tex>: | ||
| Строка 58: | Строка 58: | ||
то достаточно показать, что составленное расписание достигает этой оценки. | то достаточно показать, что составленное расписание достигает этой оценки. | ||
| − | Будем считать, что в начале алгоритма все работы упорядочены, как было сказано ранее: <tex> p_1(0) \ | + | Будем считать, что в начале алгоритма все работы упорядочены, как было сказано ранее: <tex> p_1(0) \geqslant p_2(0) \geqslant \ldots \geqslant p_n(0) </tex>. Это утверждение не меняется на протяжении всего выполнения алгоритма, для любого момента времени. Получаем: <tex> p_1(t) \geqslant p_2(t) \geqslant \ldots \geqslant p_n(t) </tex>. Докажем что алгоритм составляет расписание в соответствии с этим свойством. Чтобы доказать этот факт, будем считать что в любой момент времени <tex>T</tex> нет простоев машин, когда есть хотя бы одна невыполненная работа. Получаем: |
| − | <tex> T(s_1 + | + | <tex> T(s_1 + \ldots + s_m) = p_1 + p_2 + \ldots + p_n </tex> или <tex> T = {P_n \over S_m} </tex> |
Таким образом необходимая оценка достигается нашим алгоритмом. | Таким образом необходимая оценка достигается нашим алгоритмом. | ||
| − | Допустим хотя бы одна машина простаивает, в момент когда есть невыполненные работы, получим следующее неравенство для времен окончания работ (обозначим далее как <tex> f_i </tex>) на станках <tex>M_1 | + | Допустим хотя бы одна машина простаивает, в момент когда есть невыполненные работы, получим следующее неравенство для времен окончания работ (обозначим далее как <tex> f_i </tex>) на станках <tex>M_1 \ldots M_m</tex>, пронумерованных по убыванию скоростей: |
| − | <tex> f_1 \ | + | <tex> f_1 \geqslant f_2 \geqslant \ldots \geqslant f_m </tex> |
Докажем написанное выше неравенство: | Докажем написанное выше неравенство: | ||
| − | Предположим, что <tex> f_i < f_{i+1} </tex> для некоторого <tex> 1 \ | + | Предположим, что <tex> f_i < f_{i+1} </tex> для некоторого <tex> 1 \leqslant i \leqslant m-1 </tex>. Тогда <tex>Level</tex> последней работы, выполнявшейся на станке <tex> M_i </tex> в момент времени <tex> f_i - \varepsilon </tex> (где <tex> \varepsilon > 0</tex> достаточно мал) меньше, чем <tex>Level</tex> последней работы на станке <tex> M_{i+1} </tex>. Пришли к противоречию, так как при распределении, работы с наибольшим <tex>Level</tex> выставлялись на самые быстрые станки. |
| − | Пусть <tex> T </tex> = <tex> f_1 = f_2 = f_3 = | + | Пусть <tex> T </tex> = <tex> f_1 = f_2 = f_3 = \ldots = f_j > f_{j+1}</tex> ,где <tex> j < m </tex>. Чтобы работы завершились в момент времени <tex> T </tex>, необходимо начать их в момент времени 0, поскольку если это не выполняется, то у нас найдется работа <tex> J_i </tex> , которая начинается позже <tex> t = 0 </tex> и заканчивается в <tex> T </tex>. Это означает, что в момент времени <tex> 0 </tex> начинаются как минимум <tex> m </tex> работ. Пусть первые <tex> m </tex> работ стартовали вместе на всех машинах. Мы получаем <tex> p_1(0) \geqslant p_2(0) \geqslant \ldots \geqslant p_m(0) \geqslant p_i(0) </tex>, из чего следует, что <tex> p_1(T - \varepsilon) \geqslant \ldots \geqslant p_m(T - \varepsilon) \geqslant p_i(T - \varepsilon) > 0 </tex> для любого <tex> \varepsilon </tex>, удовлетворяющего условию <tex> 0 \leqslant \varepsilon < T - t </tex>. Таким образом, до момента времени <tex> T </tex> нет простаивающих машин. Пришли к противоречию. Получаем <tex> T = {P_j \over S_j} </tex>. |
| − | ==Пример== | + | ===Пример=== |
[[Файл:Qpmtncmax.png|600px|thumb|right|Картинка к примеру]] | [[Файл:Qpmtncmax.png|600px|thumb|right|Картинка к примеру]] | ||
| Строка 81: | Строка 81: | ||
В начальный момент времени начинаем обрабатывать работы с наибольшим временем выполнения <tex>J_1-J_3</tex> на станках <tex>M_1-M_3</tex> соответственно. В момент времени <tex>T_1</tex> <tex>lvl</tex> 1-ой работы и 2-ой работы совпадает. С этого момента начинаем обрабатывать работы <tex> J_1,J_2</tex> синхронно на станках: <tex>M_1 M_2</tex>. В момент времени <tex>T_2</tex> работа <tex>J_3</tex> опускается до уровня работы <tex>J_4</tex>.Работы <tex> J_3,J_4</tex> выполняем одновременно на одном станке <tex> M_3</tex>. В момент времени <tex>T_3</tex> начинаем выполнять первые четыре работы на всех станках одновременно, далее просто добавятся работы <tex>J_5 J_6</tex> и все работы закончатся одновременно. | В начальный момент времени начинаем обрабатывать работы с наибольшим временем выполнения <tex>J_1-J_3</tex> на станках <tex>M_1-M_3</tex> соответственно. В момент времени <tex>T_1</tex> <tex>lvl</tex> 1-ой работы и 2-ой работы совпадает. С этого момента начинаем обрабатывать работы <tex> J_1,J_2</tex> синхронно на станках: <tex>M_1 M_2</tex>. В момент времени <tex>T_2</tex> работа <tex>J_3</tex> опускается до уровня работы <tex>J_4</tex>.Работы <tex> J_3,J_4</tex> выполняем одновременно на одном станке <tex> M_3</tex>. В момент времени <tex>T_3</tex> начинаем выполнять первые четыре работы на всех станках одновременно, далее просто добавятся работы <tex>J_5 J_6</tex> и все работы закончатся одновременно. | ||
| − | ==Время работы== | + | ===Время работы=== |
<tex> Level </tex> - алгоритм вызывает функцию <tex> Assign(t) </tex> в самом худшем случае <tex>O(n)</tex> раз. Функция <tex> Assign(t) </tex> выполняется за <tex>O(nm)</tex>. Итоговое время работы <tex>O(n^2m)</tex>. | <tex> Level </tex> - алгоритм вызывает функцию <tex> Assign(t) </tex> в самом худшем случае <tex>O(n)</tex> раз. Функция <tex> Assign(t) </tex> выполняется за <tex>O(nm)</tex>. Итоговое время работы <tex>O(n^2m)</tex>. | ||
| − | == | + | ==Источники информации== |
| − | * Peter Brucker. «Scheduling Algorithms» {{---}} «Springer», 2006 г. {{---}} | + | * Peter Brucker. «Scheduling Algorithms» {{---}} «Springer», 2006 г. {{---}} 124 {{---}} 129 стр. {{---}} ISBN 978-3-540-69515-8 |
Версия 13:47, 5 июня 2016
| Задача: |
| Дано несколько станков с разной скоростью выполнения работ, работающих параллельно. Работа может быть прервана в любой момент и продолжена позже на любой машине. Необходимо минимизировать время выполнения всех работ. |
Содержание
Алгоритм построения расписания
Перед выполнением алгоритма, упорядочим все работы по убыванию их времени выполнения:, а все машины в порядке убывания скоростей: . Введем следующие обозначения:
, , - время выполнения -ой работы, - скорость работы -oй машины.
Необходимое условие для выполнения всех работ в интервале :
или
Кроме того, должно выполняться условие для всех , так как это нижняя оценка времени выполнения работ . Исходя из этого получаем нижнюю границу :
=
Перейдем к описанию алгоритма. Будем назвать -ом работы - невыполненную часть работы в момент времени
Далее построим расписание, которое достигает нашей оценки , с помощью -алгоритма.
- алгоритм:
while Assign(t) and and , and , // поиск следующего момента времени, в который нужно будет перераспределить машины/работы Построение расписания
Функция :
// множество работ с положительным level // множество всех станков while or max // максимальное значение level из J count // количество работ с level = max , работ из самых быстрых машин из Распределяем работы
Доказательство корректности алгоритма
Так как нижняя граница :
=
то достаточно показать, что составленное расписание достигает этой оценки.
Будем считать, что в начале алгоритма все работы упорядочены, как было сказано ранее: . Это утверждение не меняется на протяжении всего выполнения алгоритма, для любого момента времени. Получаем: . Докажем что алгоритм составляет расписание в соответствии с этим свойством. Чтобы доказать этот факт, будем считать что в любой момент времени нет простоев машин, когда есть хотя бы одна невыполненная работа. Получаем:
или
Таким образом необходимая оценка достигается нашим алгоритмом.
Допустим хотя бы одна машина простаивает, в момент когда есть невыполненные работы, получим следующее неравенство для времен окончания работ (обозначим далее как ) на станках , пронумерованных по убыванию скоростей:
Докажем написанное выше неравенство:
Предположим, что для некоторого . Тогда последней работы, выполнявшейся на станке в момент времени (где достаточно мал) меньше, чем последней работы на станке . Пришли к противоречию, так как при распределении, работы с наибольшим выставлялись на самые быстрые станки.
Пусть = ,где . Чтобы работы завершились в момент времени , необходимо начать их в момент времени 0, поскольку если это не выполняется, то у нас найдется работа , которая начинается позже и заканчивается в . Это означает, что в момент времени начинаются как минимум работ. Пусть первые работ стартовали вместе на всех машинах. Мы получаем , из чего следует, что для любого , удовлетворяющего условию . Таким образом, до момента времени нет простаивающих машин. Пришли к противоречию. Получаем .
Пример
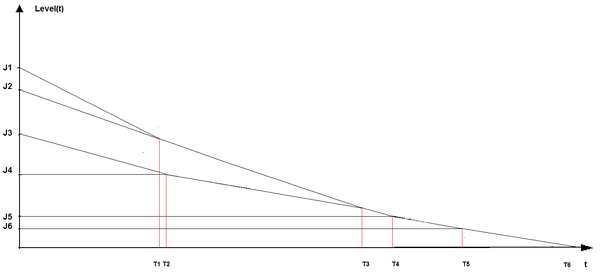
Пусть у нас есть 6 работ и 3 станка. Покажем работу алгоритма для данного случая.
В начальный момент времени начинаем обрабатывать работы с наибольшим временем выполнения на станках соответственно. В момент времени 1-ой работы и 2-ой работы совпадает. С этого момента начинаем обрабатывать работы синхронно на станках: . В момент времени работа опускается до уровня работы .Работы выполняем одновременно на одном станке . В момент времени начинаем выполнять первые четыре работы на всех станках одновременно, далее просто добавятся работы и все работы закончатся одновременно.
Время работы
- алгоритм вызывает функцию в самом худшем случае раз. Функция выполняется за . Итоговое время работы .
Источники информации
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 124 — 129 стр. — ISBN 978-3-540-69515-8