Теорема Эдмондса-Лоулера

Условие теоремы

Теорема (Эдмондса - Лоулера):

Пусть [math]M_1=\langle X, I_1\rangle[/math], [math]M_2=\langle X, I_2\rangle[/math] — матроиды. Тогда [math]\max\limits_{I \in I_1 \cap I_2 } |I| = \min\limits_{A \subseteq X} \left(r_1(A) + r_2(X \setminus A)\right)[/math]. Где [math]r_1[/math] и [math]r_2[/math] — ранговые функции в первом и втором матроиде соответственно.

Доказательство:

[math]\triangleright[/math]

Граф замен, кратчайший путь Завершение алгоритма Докажем неравенство [math]\max\limits_{I \in I_1 \cap I_2 } |I| \le \min\limits_{A \subseteq X} r_1(A) + r_2(X \setminus A)[/math] Выберем произвольные [math]I \in I_1 \cap I_2[/math], [math]A \subseteq X[/math], тогда [math]|I| = |I \cap A| + |I \cap (X \setminus A)|[/math] [math]I \cap A[/math] и [math]I \cap (X \setminus A)[/math] - независимые в обоих матроидах (как подмножества независимового [math]I[/math]), значит [math]|I| = r_1(I \cap A) + r_2(I \cap (X \setminus A))[/math] Но [math]r_1(I \cap A) \le r_1(A)[/math] и [math]r_2(I \cap (X \setminus A)) \le r_2(X \setminus A)[/math], значит [math]|I| \le r_1(A) + r_2(X \setminus A)[/math] В силу произвольности [math]I[/math] и [math]A[/math] получаем [math]\max\limits_{I \in I_1 \cap I_2 } |I| \le \min\limits_{A \subseteq X} r_1(A) + r_2(X \setminus A)[/math] Конструктивно построим [math]\forall M_1, M_2[/math] такие [math]I \in I_1 \cap I_2[/math] и [math]A \subseteq X[/math], что [math]|I| = r_1(A) + r_2(X \setminus A)[/math]. 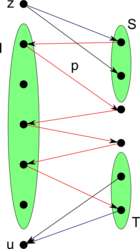Обозначим [math]S = \left\{x|I \cup \{x\} \in I_1\right\}[/math], [math]T = \left\{x|I \cup \{x\} \in I_2\right\}[/math]. Если [math]S \cap T \ne \varnothing[/math], добавим их пересечение в [math]I[/math]. Построим граф замен [math]G_I[/math]. Добавим вершину [math]z[/math], не влияющую на независимость в первом матроиде — из неё будут вести рёбра во все вершины множества [math]S[/math]. Пусть [math]p[/math] — кратчайший путь из [math]S[/math] в [math]T[/math], [math]p_1[/math] — путь [math]p[/math] с добавленным в начало ребром из [math]z[/math]. По лемме о единственном паросочетании и лемме о единственном паросочетании, индуцированном кратчайшем путём [math]I \oplus p_1 \in I_2[/math]. Теперь добавим вершину [math]u[/math], не влияющую на независимость во втором матроиде — в неё будут вести рёбра из всех вершин множества [math]T[/math]. Тогда [math]p_2[/math] (путь [math]p[/math] с добавленным ребром в [math]u[/math]) — кратчайший путь из [math]S[/math] в [math]u[/math]. Аналогично, [math]I \oplus p_2 \in I_1[/math]. Отсюда следует, что [math]I \oplus p \in I_1 \cap I_2[/math], причём [math]|I \oplus p| = |I| + 1[/math]. Будем таким образом увеличивать [math]I[/math], пока существует путь [math]p[/math]. Рассмотрим момент, когда такого пути не нашлось. Введём обозначение: [math]A = \{u|u \rightsquigarrow T\}[/math]. Докажем, что [math]r_1(A) = |I \cap A|[/math] от противного. Пусть [math]r_1(A) \gt |I \cap A|[/math], тогда существует [math]z \in A \setminus (I \cap A)[/math], такое, что [math](I \cap A) \cup \{z\} \in I_1[/math]. Если [math]I \cup \{z\} \in I_1[/math], то [math]z \in S[/math] и из [math]S[/math] есть путь в [math]A[/math]. Значит, [math]I \cup \{z\} \notin I_1[/math]. Отсюда следует, что существует [math]y \in I \setminus A[/math], такое что [math]I \setminus \{y\} \cup \{z\} \in I_1[/math]. Но тогда ребро [math]yz[/math] имеется в графе, что противоречит отсутствию пути из [math]S[/math] в [math]T[/math]. Следовательно, [math]r_1(A) = |I \cap A|[/math]. Аналогично, [math]r_2(\overline A) = |I \cap \overline A|[/math]. Отсюда [math]r_1(A) + r_2(\overline A) = |I|[/math], то есть при найденных [math]I[/math] и [math]A[/math] достигается равенство. Построен пример равенства, значит, теорема доказана.

[math]\triangleleft[/math]

Источник

Chandra Chekuri — Combinatorial Optimization