Доказательство нерегулярности языков: лемма о разрастании

Лемма (О разрастании):

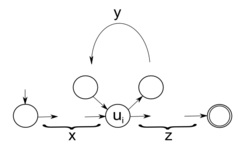
Пусть [math]L[/math] — регулярный язык над алфавитом [math]\Sigma[/math], тогда существует [math]n[/math], такой что для любого слова [math] \omega \in L[/math], длины не меньше [math] n [/math] найдутся слова [math] x,y,z \in \Sigma^*[/math], для которых верно [math]xyz=\omega, y\neq \varepsilon, |xy|\leqslant n[/math] и [math]xy^{k}z\in L[/math] для всех [math] k \geqslant 0[/math].

Доказательство:

[math]\triangleright[/math]

Пусть [math]L[/math] - регулярный язык над алфавитом [math]\Sigma[/math]. Пусть длина слов из языка ограничена, тогда полагая [math]n = \max\limits_{l \in L}|l| + 1[/math], получим пустое множество слов длины не менее [math]n[/math], откуда утверждение автоматически верно. Пусть слова из языка могут иметь сколь угодно большую длину. Т. к. регулярный язык является автоматным тогда найдётся автомат [math]A[/math], допускающий язык [math]L[/math]. Обозначим размер автомата [math]A[/math], как [math]n[/math]. В языке [math]L[/math] найдётся слово [math]\omega[/math] длины не меньше [math]n[/math]. Рассмотрим переходы в автомате [math]\langle s,\omega\rangle \vdash\langle u_1, \omega[0]^{-1}\omega\rangle\vdash\dots\vdash\langle u_{l},\epsilon\rangle, \: l\geqslant n[/math]. Так как [math]l[/math] не меньше количества состояний в автомате [math]n[/math], то в переходах будет совпадение. Пусть [math]u_i[/math] и [math]u_j[/math] - первое совпадение. Тогда в нашем слове [math]\omega[/math] можно размножить кусок, который отвечает за переход, от состояния [math]u_i[/math] к состоянию [math]u_j[/math]. То есть если верно [math]\langle s, xyz\rangle \vdash^*\langle u_i, yz\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle[/math], то тогда верно [math]\langle s, xy^kz\rangle \vdash^*\langle u_i, y^kz\rangle\vdash^*\langle u_j, y^{k-1}z\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle[/math]. Тогда автомат [math]A[/math] допускает слово [math]xy^kz[/math], следовательно [math]xy^kz[/math] принадлежит регулярному языку [math]L[/math].

[math]\triangleleft[/math]

Замечание. Условие леммы не является достаточным для регулярности языка.

Доказательства нерегулярности языков

Для доказательства нерегулярности языка можно использовать свойства регулярных и автоматных языков.
Часто удобно использовать отрицание леммы о разрастании. Пусть [math]L[/math] - язык над алфавитом [math]\Sigma[/math]. Если для любого натурального [math]n[/math] найдётся такое слово [math]\omega[/math] из данного языка, что его длина будет не меньше [math] n[/math] и при любом разбиении на три слова [math]x,y,z[/math] такие, что [math]y[/math] непустое и длина [math]xy[/math] не больше [math]n[/math], существует такое [math]k[/math], что [math]xy^kz \notin L[/math], то язык [math]L[/math] - не регулярный.

Нерегулярность языка правильных скобочных последовательностей

Пусть дан какой-то [math]n[/math] для него предъявляем слово [math]\omega=(^n)^n[/math]. После этого слово [math]\omega[/math] как-то разбили на [math]x, y, z[/math]. Так как [math]|xy|\leqslant n[/math], то из-за выбранного слова [math]y=(^b[/math], где [math]b[/math] больше нуля. Для любого такого разбиения берём [math]k=2[/math] и получаем [math]xy^kz=(^{n+b})^n[/math], что не является правильной скобочной последовательностью. Значит язык правильных скобочных последовательностей не регулярный язык.

Нерегулярность языка [math]\{0^a1^a\}_{a\geqslant 0}[/math]

Пусть дан какой-то [math]n[/math] для него предъявляем слово [math]\omega=0^n1^n[/math]. После этого слово [math]\omega[/math] как-то разбили на [math]x, y, z[/math]. Так как [math]|xy|\leqslant n[/math], то из-за выбранного слова [math]y=0^b[/math], где [math]b[/math] больше нуля. Для любого такого разбиения берём [math]k=2[/math] и получаем [math]xy^kz=0^{n+b}1^n[/math], что не является элементом множества слов языка [math]\{0^a1^a\}_{a\geqslant 0}[/math], значит этот язык не регулярен.

См. также

• Лемма о разрастании для КС-грамматик
• Интерпретация булевых формул с кванторами как игр для двух игроков

Литература

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)