Детерминированные автоматы с магазинной памятью, допуск по пустому стеку — различия между версиями
(Новая страница: «{{Определение |definition = Определим <b>детерминированный автомат с магазинной памятью, допуска…») |
Kirillova (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Определим <b>детерминированный автомат с магазинной памятью, допускающий по пустому стеку</b>, как [[Детерминированные_автоматы_с_магазинной_памятью|детерминированный автомат с магазинной памятью]], у которого нет множества <tex> | + | Определим <b>детерминированный автомат с магазинной памятью, допускающий по пустому стеку</b>, как [[Детерминированные_автоматы_с_магазинной_памятью|детерминированный автомат с магазинной памятью]], у которого нет множества <tex>T</tex> допускающих состояний. Автомат заканчивает свою работу как только стек становится пустым. |
}} | }} | ||
| + | Определим для него множество допускающих слов <tex>N = \{\omega | (q_0,a_0,Z_0)\vdash^* (p,\epsilon,\epsilon)\}</tex>, где <tex>p</tex> {{---}} произвольное состояние. | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Язык называется <b>беспрефиксным</b>, если | + | Язык называется <b>беспрефиксным</b>, если для любой пары слов из этого языка ни одно из этих слов не является префиксом другого. |
}} | }} | ||
{{Теорема | {{Теорема | ||
Версия 00:39, 2 декабря 2011
| Определение: |
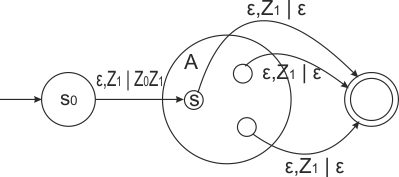
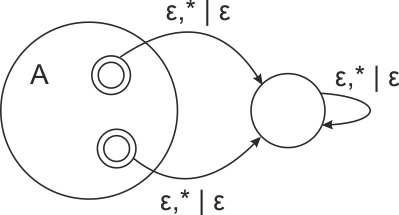
| Определим детерминированный автомат с магазинной памятью, допускающий по пустому стеку, как детерминированный автомат с магазинной памятью, у которого нет множества допускающих состояний. Автомат заканчивает свою работу как только стек становится пустым. |
Определим для него множество допускающих слов , где — произвольное состояние.
| Определение: |
| Язык называется беспрефиксным, если для любой пары слов из этого языка ни одно из этих слов не является префиксом другого. |